This may not be an all-time record-breaking day according to Environment Canada (supposedly, the peak temperature today at Ottawa Airport was 34.8 C at 2 PM) but it sure is hot.
You could be forgiven if you thought that this measurement is of the body temperature of a COVID-19 patient with mild symptoms, not the outdoor temperature on our balcony, measured in the shade:
As I said… really hot. Praise be to air conditioning.
Long overdue, but I just finished preparing the latest Maxima release, version 5.44.
I am always nervous when I do this. It is one thing to mess with my own projects, it is another thing to mess with a project that is the work of many people and contains code all the way back from the 1960s.
In case anyone doubted that modern birds are descendants of dinosaurs, here is a reminder: the shoebill.
These amazing creatures are apparently quite docile with humans, but eat baby crocodiles for lunch, which they kill by decapitating them.
They really look like survivors of the K-T asteroid impact. They are… I think they are beautiful.
I don’t always like commercial publishers. Some of their textbooks are prohibitively expensive, yet often lacking in quality. (One persistent exception is Dover Publications, who published some of the best textbooks I own, as low-cost paperbacks.)
Last night, however, I was very pleasantly surprised by Springer, who made several hundred textbooks across a range of disciplines available for free, on account of COVID-19.
I did not get greedy. I didn’t download titles indiscriminately. But I did find several titles that are of interest to me, and I gladly took advantage of this opportunity.
Thank you, Springer.
I am one of the maintainers of the Maxima computer algebra system. Maxima’s origins date back to the 1960s, when I was still in kindergarten. I feel very privileged that I can participate in the continuing development of one of the oldest continuously maintained software system in wide use.
It has been a while since I last dug deep into the core of the Maxima system. My LISP skills are admittedly a bit rusty. But a recent change to a core Maxima capability, its ability to create Taylor-series expansions of expressions, broke an important feature of Maxima’s tensor algebra packages, so it needed fixing.
The fix doesn’t amount to much, just a few lines of code:
It did take more than a few minutes though to find the right (I hope) way to implement this fix.
Even so, I had fun. This is the kind of programming that I really, really enjoy doing. Sadly, it’s not the kind of programming for which people usually pay you Big Bucks… Oh well. The fun alone was worth it.
One of the most fortunate moments in my life occurred in the fall of 2005, when I first bumped into John Moffat, a physicist from The Perimeter Institute in Waterloo, Ontario, Canada, when we both attended the first Pioneer Anomaly conference hosted by the International Space Science Institute in Bern, Switzerland.
This chance encounter turned into a 15-year collaboration and friendship. It was, to me, immensely beneficial: I learned a lot from John who, in his long professional career, has met nearly every one of the giants of 20th century physics, even as he made his own considerable contributions to diverse areas ranging from particle physics to gravitation.
In the past decade, John also wrote a few books for a general audience. His latest, The Shadow of the Black Hole, is about to be published; it can already be preordered on Amazon. In their reviews, Greg Landsberg (CERN), Michael Landry (LIGO Hanford) and Neil Cornish (eXtreme Gravity Institute) praise the book. As I was one of John’s early proofreaders, I figured I’ll add my own.
John began working on this manuscript shortly after the announcement by the LIGO project of the first unambiguous direct detection of gravitational waves from a distant cosmic event. This was a momentous discovery, opening a new chapter in the history of astronomy, while at the same time confirming a fundamental prediction of Einstein’s general relativity. Meanwhile, the physics world was waiting with bated breath for another result: the Event Horizon Telescope collaboration’s attempt to image, using a worldwide network of radio telescopes, either the supermassive black hole near the center of our own Milky Way, or the much larger supermassive black hole near the center of the nearby galaxy M87.
Bookended by these two historic discoveries, John’s narrative invites the reader on a journey to understand the nature of black holes, these most enigmatic objects in our universe. The adventure begins in 1784, when the Reverend John Michell, a Cambridge professor, speculated about stars so massive and compact that even light would not be able to escape from its surface. The story progresses to the 20th century, the prediction of black holes by general relativity, and the strange, often counterintuitive results that arise when our knowledge of thermodynamics and quantum physics is applied to these objects. After a brief detour into the realm of science-fiction, John’s account returns to the hard reality of observational science, as he explains how gravitational waves can be detected and how they fit into both the standard theory of gravitation and its proposed extensions or modifications. Finally, John moves on to discuss how the Event Horizon Telescope works and how it was able to create, for the very first time, an actual image of the black hole’s shadow, cast against the “light” (radio waves) from its accretion disk.
John’s writing is entertaining, informative, and a delight to follow as he accompanies the reader on this fantastic journey. True, I am not an unbiased critic. But don’t just take my word for it; read those reviews I mentioned at the beginning of this post, by preeminent physicists. In any case, I wholeheartedly recommend The Shadow of the Black Hole, along with John’s earlier books, to anyone with an interest in physics, especially the physics of black holes.
Heaven knows why I sometimes get confused by the simplest things.
In this case, the conversion between two commonly used cosmological coordinate systems: Comoving coordinates vs. coordinates that are, well, not comoving, in which cosmic expansion is ascribed to time dilation effects instead.
In the standard coordinates that are used to describe the homogeneous, isotropic universe of the Friedmann–Lemaître–Robertson–Walker (FLRW) metric, the metric is given by
$$ds^2=dt^2-a^2dR^2,$$
where \(a=a(t)\) is a function of the time coordinate, and \(R\) represents the triplet of spatial coordinates: e.g., \(dR^2=dx^2+dy^2+dz^2.\)
I want to transform this using \(R’=aR,\) i.e., transform away the time-dependent coefficient in front of the spatial term in the metric. The confusion comes because for some reason, I always manage to convince myself that I also have to make the simultaneous replacement \(t’=a^{-1}dt.\)
I do not. This is nonsense. I just need to introduce \(dR’\). The rest then presents itself automatically:
$$\begin{align*}
R’&=aR,\\
dR&=d(a^{-1}R’)=-a^{-2}\dot{a}R’dt+a^{-1}dR’,\\
ds^2&=dt^2-a^2[-a^{-2}\dot{a}R’dt+a^{-1}dR’]^2\\
&=(1-a^{-2}\dot{a}^2{R’}^2)dt^2+2a^{-1}\dot{a}R’dtdR’-d{R’}^2\\
&=(1-H^2{R’}^2)dt^2+2HR’dtdR’-d{R’}^2,
\end{align*}$$
where \(H=\dot{a}/a\) as usual.
OK, now that I recorded this here in my blog for posterity, perhaps the next time I need it, I’ll remember where to find it. For instance, the next time I manage to stumble upon one of my old Quora answers that, for five and a half years, advertised my stupidity to the world by presenting an incorrect answer on this topic.
This, incidentally, would serve as a suitable coordinate system representing the reference frame of an observer at the origin. It also demonstrates that such an observer sees an apparent horizon, the cosmological horizon, given by \(1-H^2{R’}^2=0,\), i.e., \(R’=H^{-1},\) the distance characterized by the inverse of the Hubble parameter.
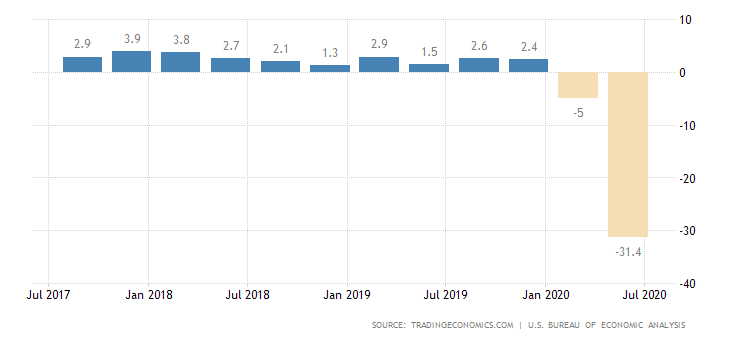
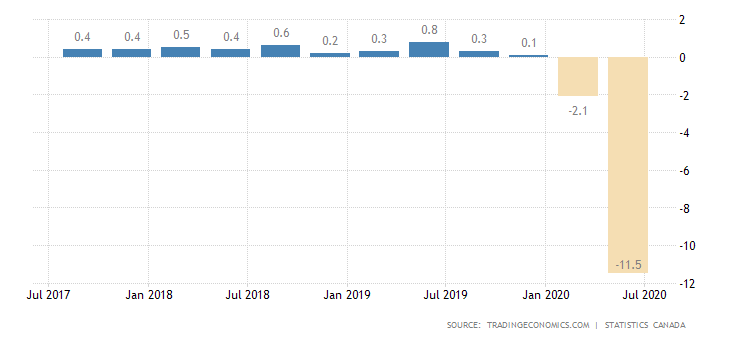
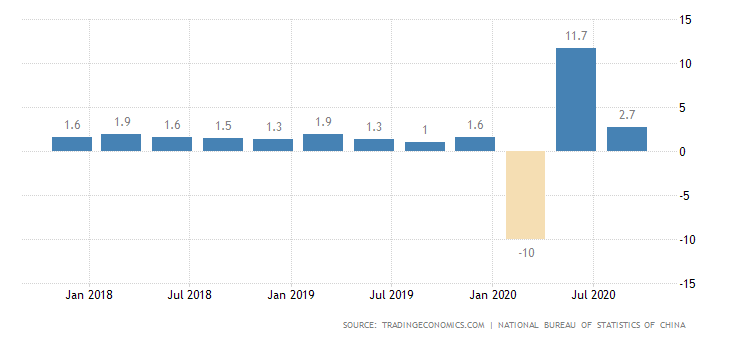So here I am, reading about some trivial yet not-so-trivial probability distributions.
Let’s start with the uniform distribution. Easy-peasy, isn’t it: a random number, between 0 and 1, with an equal probability assigned to any value within this range.
So… what happens if I take two such random numbers and add them? Why, I get a random number between 0 and 2 of course. But the probability distribution will no longer be uniform. There are more ways to get a value in the vicinity of 1 than near 0 or 2.
And what happens if I add three such random numbers? Or four? And so on?
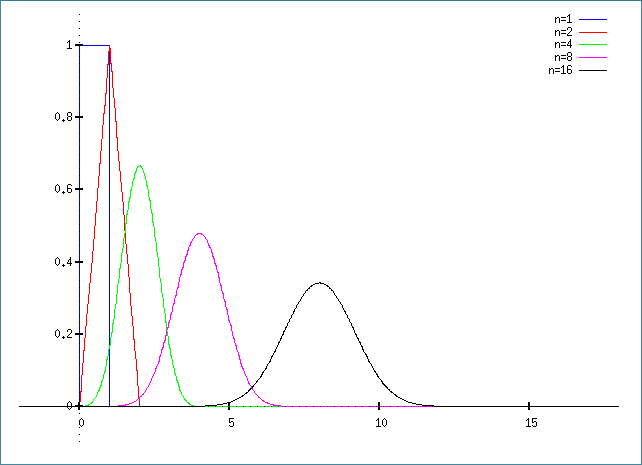
The statistics of this result are captured by the Irwin-Hall distribution, defined as
$$f_{\rm IH}(x,n)=\dfrac{1}{2(n-1)!}\sum\limits_{k=1}^n(-1)^k\begin{pmatrix}n\\k\end{pmatrix}(x-k)^{n-1}{\rm sgn}(x-k).$$
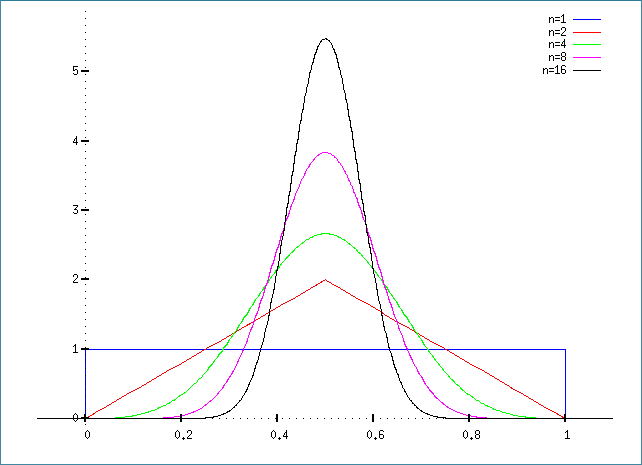
OK, so that’s what happens when we add these uniformly generated random values. What happens when we average them? This, in turn, is captured by the Bates distribution, which, unsurprisingly, is just the Irwin-Hall distribution, scaled by the factor \(n\):
$$f_{\rm B}(x,n)=\dfrac{n}{2(n-1)!}\sum\limits_{k=1}^n(-1)^k\begin{pmatrix}n\\k\end{pmatrix}(nx-k)^{n-1}{\rm sgn}(nx-k).$$
How about that.
For what it’s worth, here is the Maxima script to generate the Irwin-Hall plot:
fI(x,n):=1/2/(n-1)!*sum((-1)^k*n!/k!/(n-k)!*(x-k)^(n-1)*signum(x-k),k,0,n);
plot2d([fI(x,1),fI(x,2),fI(x,4),fI(x,8),fI(x,16)],[x,-2,18],[box,false],
[legend,"n=1","n=2","n=4","n=8","n=16"],[y,-0.1,1.1]);
And this one for the Bates plot:
fB(x,n):=n/2/(n-1)!*sum((-1)^k*n!/k!/(n-k)!*(n*x-k)^(n-1)*signum(n*x-k),k,0,n);
plot2d([fB(x,1),fB(x,2),fB(x,4),fB(x,8),fB(x,16)],[x,-0.1,1.1],[box,false],
[legend,"n=1","n=2","n=4","n=8","n=16"],[y,-0.1,5.9]);
Yes, I am still a little bit of a math geek at heart.
My lovely wife, Ildiko, woke up from a dream and asked: If you have a flower with 7 petals and two colors, how many ways can you color the petals of that flower?
Intriguing, isn’t it.
Such a flower shape obviously has rotational symmetry. Just because the flower is rotated by several times a seventh of a revolution, the resulting pattern should not be counted as distinct. So it is not simply calculating what number theorists call the \(n\)-tuple. It is something more subtle.
We can, of course, start counting the possibilities the brute force way. It’s not that difficult for a smaller number of petals, but it does get a little confusing at 6. At 7 petals, it is still something that can be done, but the use of paper-and-pencil is strongly recommended.
So what about the more general case? What if I have \(n\) petals and \(k\) colors?
Neither of us could easily deduce an answer, so I went to search the available online literature. For a while, other than finding some interesting posts about cyclic, or circular permutations, I was mostly unsuccessful. In fact, I began to wonder if this one was perhaps one of those embarrassing little problems in combinatorial mathematics that has no known solution and about which the literature remains strangely quiet.
But then I had another idea: By this time, we both calculated the sequence, 2, 3, 4, 6, 8, 14, 20, which is the number of ways flowers with 1, 2, …, 7 petals can be colored using only two colors. Surely, this sequence is known to Google?
Indeed it is. It turns out to be a well-known sequence in the online encyclopedia of integer sequences, A000031. Now I was getting somewhere! What was especially helpful is that the encyclopedia mentioned necklaces. So that’s what this problem set is called! Finding the Mathworld page on necklaces was now easy, along with the corresponding Wikipedia page. I also found an attempt, valiant though only half-successful if anyone is interested in my opinion, to explain the intuition behind this known result:
$$N_k(n)=\frac{1}{n}\sum_{d|n}\phi(d)k^{n/d},$$
where the summation is over all the divisors of \(n\), and \(\phi(d)\) is Euler’s totient function, the number of integers between \(1\) and \(d\) that are relative prime to \(d\).
Evil stuff if you asked me. Much as I always liked mathematics, number theory was not my favorite.
In the case of odd primes, such as the number 7 that occurred in Ildiko’s dream, and only two colors, there is, however, a simplified form:
$$N_2(n)=\frac{2^{n-1}-1}{n}+2^{(n-1)/2}+1.$$
Unfortunately, this form is for “free necklaces”, which treats mirror images as equivalent. For \(n<6\) it makes no difference, but substituting \(n=7\), we get 18, not 20.
Finally, a closely related sequence, A000029, characterizes necklaces that can be turned over, that is to say, the case where we do not count mirror images separately.
Oh, this was fun. It’s not like I didn’t have anything useful to do with my time, but it was nonetheless a delightful distraction. And a good thing to chat about while we were eating a wonderful lunch that Ildiko prepared today.
Our most comprehensive paper yet on the Solar Gravitational Lens is now online.
This was a difficult paper to write, but I think that, in the end, it was well worth the effort.
We are still investigating the spherical Sun (the gravitational field of the real Sun deviates ever so slightly from spherical symmetry, and that can, or rather it will, have measurable effects) and we are still considering a stationary target (as opposed to a planet with changing illumination and surface features) but in this paper, we now cover the entire image formation process, including models of what a telescope sees in the SGL’s focal region, how such observations can be stitched together to form an image, and how that image compares against the inevitable noise due to the low photon count and the bright solar corona.
I just saw the news: Alexei Leonov died.
Leonov was a Soviet cosmonaut. The first man to ever take a spacewalk (which, incidentally, nearly killed him, as did his atmospheric re-entry, which didn’t exactly go as planned either.)
Leonov was also an accomplished artist. Many of his paintings featured space travel. Here is a beautiful picture, from a blog entry by Larry McGlynn, showing Leonov with one of his paintings, in 2004 in Los Angeles.
So Leonov now joins that ever growing list of brave souls from the dawn of the space age who are no longer with us. Rest in peace, Major General Leonov.
I just came across this XKCD comic.
Though I can happily report that so far, I managed to avoid getting hit by a truck, it is a life situation in which I found myself quite a number of times in my life.
In fact, ever since I’ve seen this comic an hour or so ago, I’ve been wondering about the resistor network. Thankfully, in the era of the Internet and Google, puzzles like this won’t keep you awake at night; well-reasoned solutions are readily available.
Anyhow, just in case anyone wonders, the answer is 4/π − 1/2 ohms.
Yesterday, we posted our latest paper on arXiv. Again, it is a paper about the solar gravitational lens.
This time around, our focus was on imaging an extended object, which of course can be trivially modeled as a multitude of point sources.
However, it is a multitude of point sources at a finite distance from the Sun.
This adds a twist. Previously, we modeled light from sources located at infinity: Incident light was in the form of plane waves.
But when the point source is at a finite distance, light from it comes in the form of spherical waves.
Now it is true that at a very large distance from the source, considering only a narrow beam of light, we can approximate those spherical waves as plane waves (paraxial approximation). But it still leaves us with the altered geometry.
But this is where a second observation becomes significant: As we can intuit, and as it is made evident through the use of the eikonal approximation, most of the time we can restrict our focus onto a single ray of light. A ray that, when deflected by the Sun, defines a plane. And the investigation can proceed in this plane.
The image above depicts two such planes, corresponding to the red and the green ray of light.
These rays do meet, however, at the axis of symmetry of the problem, which we call the optical axis. However, in the vicinity of this axis the symmetry of the problem is recovered, and the result no longer depends on the azimuthal angle that defines the plane in question.
To make a long story short, this allows us to reuse our previous results, by introducing the additional angle β, which determines, among other things, the additional distance (compared to parallel rays of light coming from infinity) that these light rays travel before meeting at the optical axis.
This is what our latest paper describes, in full detail.
The world is celebrating the 50th anniversary of one of the most momentous events in human history: the first time a human being set foot on another celestial body.
It is also a triumph of American ingenuity. Just as Jules Verne predicted a century earlier, it was America’s can-do spirit that made the Moon landing, Armstrong’s “one small step” possible.
And today, just like 50 years ago, their success was celebrated around the world, by people of all nationality, religion, gender or ethnicity.
But that’s not good enough for some New York Times columnists.
Instead of celebrating the Moon landing, Mary Robinette Kowal complains about the gender bias that still exists in the space program. Because, as we learn from her article, this evil male chauvinistic space program was “designed by men, for men”. Because, you know, men sweat in different areas of their body and all. Even in the office, temperatures are set for men, which leaves women carrying sweaters.
Sophie Pinkham goes further. Instead of celebrating America’s success on July 20, 1969, Pinkham goes on to praise the Soviet space program in a tone that might have been rejected even by the editors of Pravda in 1969 as too over-the-top. Because unlike America, the Soviets put the first woman in space! Their commitment to equality did not stop there: They also sent the first Asian man and the first black man into orbit. Because, we are told, “under socialism, a person of even the humblest origins could make it all the way up.”
Just to be clear, I am not blind to gender bias. We may have come a long way since the 1960s, but full gender equality has not yet been achieved anywhere: not in the US, not in Canada, not even in places like Iceland. And racism in America remains a palpable, everyday reality. Back in 1969, things were a lot worse.
But to pick the 50th anniversary of an event that, even back in the turbulent 1960s, had the power to unify humanity, to launch such petty rants? That is simply disgraceful. Or, as the New York Post described it, obscene.
The New York Post also makes mention of one of the female pioneers of the US space program, Margaret Hamilton, whose work was instrumental in making the Apollo landings possible. Yet somehow, neither Pinkham nor Kowal found it in their hearts to mention her name.
I have to wonder: Are columnists like Pinkham or Kowal secretly rooting for Donald Trump? Because they certainly seem to be doing their darnedest best to alienate as many voters as possible, from what appears to be an increasingly bitter, intolerant, ideological agenda on the American political left.
Fifty years ago today, fifty years ago this very hour in fact, at 9:32 AM EDT on July 16, 2019, Apollo 11 was launched.
Moonbound Apollo 11 clears the launch tower. NASA photo
And thus began a journey that, arguably, remains the greatest adventure in human history to date.
I was six years old in 1969, hooked on the novels of Jules Verne. With Apollo 11, Verne’s bold imagination became the reality of the day.
Galileo is the world’s third global satellite navigation system, built by the European Union, operating in parallel with the American GPS system and Russia’s GLONASS. It has been partially operational since 2016, with a full constellation if satellites expected to enter service this year.
But as of early Monday, July 15, Galileo has been down for nearly four days, completely inoperative in fact:
As of the time of this writing, no explanation is being offered, other than one article mentioning an unspecified issue with Galileo’s ground-based infrastructure.
It really is difficult to comprehend how such a failure can occur.
It is even more difficult to comprehend the silence, the lack of updates, explanations, or any information about the expected recovery.
And before I forget: Last week, wearing my release manager hat I successfully created a new version of Maxima, the open-source computer algebra system. As a result, Maxima is again named one of SourceForge’s projects of the week, for the week of June 10.
The release turned out to be more of an uphill battle than I anticipated, but in the end, I think everything went glitch-free.
Others have since created installers for different platforms, including Windows.
And I keep promising myself that when I grow up, I will one day understand exactly what git does and how it works, instead of just blindly following arcane scripts…
Here is a thought that has been bothering me for some time.
We live in a universe that is subject to accelerating expansion. Galaxies that are not bound gravitationally to our Local Group will ultimately vanish from sight, accelerating away until the combination of distance and increasing redshift will make their light undetectable by any imaginable instrument.
Similarly, accelerating expansion means that there will be a time in the very distant future when the cosmic microwave background radiation itself will become completely undetectable by any conceivable technological means.
In this very distant future, the Local Group of galaxies will have merged already into a giant elliptical galaxy. Much of this future galaxy will be dark, as most stars would have run out of fuel already.
But there will still be light. Stars would still occasionally form. Some dwarf stars will continue to shine for trillions of years, using their available fuel at a very slow rate.
Which means that civilizations might still emerge, even in this unimaginably distant future.
And when they do, what will they see?
They will see themselves as living in an “island universe” in an otherwise empty, static cosmos. In short, precisely the kind of cosmos envisioned by many astronomers in the early 1920s, when it was still popular to think of the Milky Way as just such an island universe, not yet recognizing that many of the “spiral nebulae” seen through telescopes are in fact distant galaxies just as large, if not larger, than the Milky Way.
But these future civilizations will see no such nebulae. There will be no galaxies beyond their “island universe”. No microwave background either. In fact, no sign whatsoever that their universe is evolving, changing with time.
So what would a scientifically advanced future civilization conclude? Surely they would still discover general relativity. But would they believe its predictions of an expanding cosmos, despite the complete lack of evidence? Or would they see that prediction as a failure of the theory, which must be remedied?
In short, how would they ever come into possession of the knowledge that their universe was once young, dense, and full of galaxies, not to mention background radiation?
My guess is that they won’t. They will have no observational evidence, and their theories will reflect what they actually do see (a static, unchanging island universe floating in infinite, empty space).
Which raises the rather unnerving, unpleasant question: To what extent exist already features in our universe that are similarly unknowable, as they can no longer be detected by any conceivable instrumentation? Is it, in fact, possible to fully understand the physics of the universe, or are we already doomed to never being able to develop a full picture?
I find this question surprisingly unnerving and depressing.
The Globe and Mail managed to publish today one of the saddest editorial cartoons I ever saw:
There really is nothing that I can add. The cartoon speaks for itself.
My research is unsupported. That is to say, with the exception of a few conference invitations when my travel costs were covered, I never received a penny for my research on the Pioneer Anomaly and my other research efforts.
Which is fine, I do it for fun after all. Still, in this day and age of crowdfunding, I couldn’t say no to the possibility that others, who find my efforts valuable, might choose to contribute.
Hence my launching of a Patreon page. I hope it is well-received. I have zero experience with crowdfunding, so this really is a first for me. Wish me luck.
