Modified Gravity
Ever since it has been established in the 1930s that Newton’s or Einstein’s theory cannot account for the orbital velocities stars in the outer regions of a spiral galaxy, there has been an interest in modifying gravity theory.
If successful, a modified gravity theory would do away with the need for dark matter. Instead, the anomalous velocities of stars far from a galactic center would be accounted for by a deviation from Newton’s or Einstein’s predictions at large distances.
A successful modified gravity theory has to clear many hurdles, among them:
- Stability: A gravity theory is not very useful if it cannot account for the stability of stars and planets, planetary systems, or galaxies.
- Solar system tests: Gravity theory has been tested to high precision in terrestrial laboratories and within the solar system.
- Galaxy rotations: Galaxy rotations follow a simple empirical relationship known as the Tully-Fisher law. To do away with dark matter, a modified gravity theory must be able to predict this relationship.
- Galaxy cluster masses: The motion of galaxies in gravitationally bound galaxy clusters must be accounted for by a cluster mass profile that does not require matter in excess of the known amount of baryonic matter.
- Gravitational lensing: The lensing profile of galaxy clusters has to be accounted for in a manner consistent with the visible distribution of matter (stars and galaxies, X-ray emitting gas).
- Cosmology: Precision measurements of the cosmic microwave background, measurements of the mass power spectrum through the distribution of galaxies, and the luminosity-distance relationship of Type Ia supernovae are three important observational tests of cosmology. The standard model of cosmology can account for these, but a modified gravity theory may have difficulties.
Yes, Einstein had it easy a hundred years ago. Today, with all the observational data at hand, the bar is set much higher. Why, we might ask, would one even bother with a modified gravity theory then, if the standard model of cosmology works so well? Simple: in the standard model, 96% of the universe is invisible, undetectable, or both. Surely that is a good enough reason.
Without further ado, there is a modified gravity theory that successfully meets these challenges (at least as far as we know.) It is called MOG, and it grew out of research by Moffat into nonsymmetric gravitational theory. MOG is a field theory. Its basic postulate is a field theory Lagrangian that, in addition to the standard Einstein-Hilbert term, incorporates a massive vector field. This massive vector field results in a repulsive gravitational force that cancels out gravity at short range. In other words, rather than making gravity stronger at large distances, MOG does the opposite: it assumes that gravity was stronger all along, but at shorter distances (galactic, subgalactic, or smaller scales) much of that strength is canceled out by the repulsive force.
The mass of the MOG vector field and its strength are governed by two constants. In MOG, these two constants, as well as Newton’s gravitational constant G are running; they are promoted to scalar fields. Thus the full MOG Lagrangian consists of the Einstein-Hilbert tensor term describing ordinary gravity; the massive vector term describing the repulsive force; three massless scalar fields; and potentials associated with the vector field and the three scalar fields. (For this reason, MOG has also been known by the acronym STVG, which stands for Scalar-Tensor-Vector Gravity theory.)
The result is a theory that is in good agreement with observation at scales ranging from the laboratory all the way to cosmology. In the solar system, and up to the scale of star clusters, MOG predicts no observable deviation from Einstein gravity. On the scale of galaxies, MOG correctly predicts the Tully Fisher law of galaxy rotation curves. On even larger scales, MOG is consistent with the lensing and mass distribution of galaxy clusters. MOG is fitted to the precision acoustic power spectrum of the cosmic microwave background, it is consistent with the luminosity-distance relationship of Type Ia supernovae, and it correctly reproduces the matter power spectrum of galaxy distributions. The latter provides an especially notable possible test of the theory: at soon-to-be-achieved data resolutions, the presence or absence of baryonic oscillations in the matter power spectrum can once and for all determine whether or not collisionless dark matter dominates the universe.
For most scenarios, the complicated field equations of MOG can be reduced to a relatively simple acceleration law that reads:
$$\frac{d^2r}{dt^2}=-\frac{GM}{r^2}+\frac{G-G_N}{r^2}M\left(1+\frac{r}{r_0}\right)e^{-r/r_0},$$
where \(G_N\) is the Newtonian acceleration, while the parameters \(G\) and \(r_0\) are given by:
\begin{align}
G&=G_N+(G_\infty-G_N)\frac{M}{(\sqrt{M}+E)^2},\qquad(G_\infty\simeq 20G_N, ~E\simeq 25000~M_\odot^{1/2}),\\
r_0&=\frac{\sqrt{M}}{D},\qquad(D\simeq 6250~M_\odot^{1/2}{\rm kpc}^{-1}),
\end{align}
and can be plotted as follows:
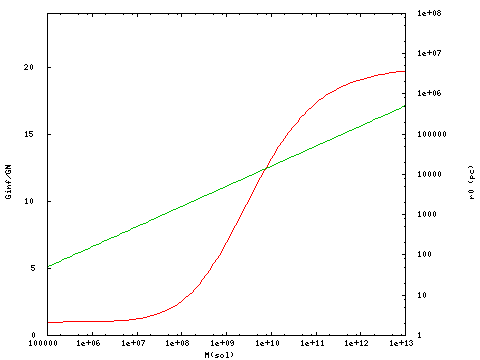
The \(G\) (red) and \(r_0\) (green) parameters of MOG.
MOG and its physical consequences are worked out in a series of papers by Moffat and others, dating back to 1979. Some of the more important and current papers are:
- Nonsymmetric Gravitational Theory.
J. W. Moffat, Phys. Lett. B, Vol 355, No 3-4, 447-452 (1995).
NGT was the original version of the theory. - Galaxy Rotation Curves Without Non-Baryonic Dark Matter.
J. R. Brownstein and J. W. Moffat, The Astrophysical Journal, Volume 636, Issue 2, pp. 721-741.
This paper describes the immediate predecessor of STVG, MSTG (Metric-Skew-Tensor-Gravity), and applies its observational consequences (which are the same as those of STVG) to galaxy rotation, finding good agreement with the data of over 100 galaxies. - Galaxy cluster masses without non-baryonic dark matter.
J. R. Brownstein and J. W. Moffat. Monthly Notices of the Royal Astronomical Society, Volume 367, Issue 2, pp. 527-540.
Still using MSTG, this paper derives the mass profile of galaxy clusters, finding good agreement with data from over 100 clusters. - Scalar tensor vector gravity theory.
J. W. Moffat. Journal of Cosmology and Astroparticle Physics, Issue 03, pp. 004 (2006).
This paper introduces the STVG version of MOG. - The Bullet Cluster 1E0657-558 evidence shows modified gravity in the absence of dark matter.
J. R. Brownstein and J. W. Moffat. MNRAS 382 (2007) 29-47.
This paper, which earned a press release by the Royal Astronomical Society, offers detailed calculations that demonstrate that the so-called Bullet Cluster, supposedly a “smoking gun” proof that dark matter exists, in fact can be easily accounted for using MOG. - Modified Gravity: Cosmology without dark matter or Einstein’s cosmological constant.
J. W. Moffat and V. T. Toth. eprint arXiv:0710.0364.
In this paper, the cosmological consequences of MOG are explored. MOG is found to be consistent with the acoustic power spectrum of the cosmic microwave background, the luminosity-distance relationship of Type Ia supernovae, and the matter power spectrum. - Fundamental parameter-free solutions in Modified Gravity.
J. W. Moffat and V. T. Toth. Class. Quant. Grav. 26 (2009) 085002.
This paper offers a solution of the MOG field equations that no longer relies on fitted parameters, putting MOG on the route towards becoming a theory with real predictive power. This is a key paper that contains our most important results.
- The bending of light and lensing in modified gravity.
J. W. Moffat and V. T. Toth. eprint arXiv:0805.4774. MNRAS 397 (2009) 1885-1992.
This paper explores in detail the relativistic bending of light in a MOG field. It takes a few tentative steps towards deriving a MOG solution for an extended distribution of matter. - Modified gravity and the origin of inertia.
J. W. Moffat and V. T. Toth. MNRAS Letters 395 (2009) L25-L28.
One curious consequence of MOG is that the theory violates Birkhoff’s theorem: a test particle inside a spherically symmetric shell of matter experiences a force. Can this force account for inertia, in line with Mach’s principle? This paper explores this possibility and finds a possible violation of the equivalence principle at very small accelerations that may be experimentally testable.
[…] gravitational theory that I’ve been working on for some time with John Moffat is called STVG, or […]
[…] doesn’t make the theory the only kid on the block worth considering. Still, try proposing an alternative gravity theory: no matter how firmly rooted in real physics it is, you will be fighting an uphill […]
[…] has extremely important implications for our work on MOG. So far, we have obtained a vacuum solution that appears consistent with observations on scales […]
[…] been investigating with John Moffat these past few years. If true, this work would imply that that our Scalar-Tensor-Vector Gravity (STVG) is in fact an effective theory (which is not necessarily surprising). Its vector and scalar […]
“… an interest in modifying gravitational theory.” The way I see things, there are two basic approaches to modifying Einstein’s field equations: (1) the equivalence principle is true and non-Einsteinian deviations from the field equations are due to wave interactions among alternate universes or (2) the equivalence principle is not true.
There is a possibility that the acceleration is independent of the nature of the body but THERE IS A SYSTEMATIC DEVIATION between the inertial mass-energy and gravitational mass-energy. Consider Einstein’s field equations: R(mu,nu) + (-1/2) * g(mu,nu) * R = – κ * T(mu,nu) – Λ * g(mu,nu) — what might be wrong? Consider the possible correction R(mu,nu) + (-1/2 + dark-matter-compensation-constant) * g(mu,nu) * R = – κ * (T(mu,nu) / equivalence-principle-failure-factor) – Λ * g(mu,nu), where equivalence-principle-failure-factor = (1 – (T(mu,nu)/T(max))^2)^(1/2) — if dark-matter-compensation-constant = 0 and T(max) = +∞ then Einstein’s field equations are recovered.
I don’t believe that sticking to the equivalence principle implies “wave interactions among alternate universes”, whatever that even means. By way of the simplest example, Jordan-Brans-Dicke theory is a perfectly decent modification of Einstein’s theory that leaves the equivalence principle alone.
Your proposed modification, forgive me, is nonsensical. The 1/2 on the LHS is not accidental; it arises from the action principle. Change it and the LHS is no longer conserved. Your “equivalence-principle-failure-factor” amounts to a rescaling of the gravitational constant \(\kappa\), and as such, it is just a variation on the Jordan-Brans-Dicke theme.
There are ways to introduce modifications that violate the equivalence principle into the theory through the action principle. This is a well-studied subject. Ultimately though, a theory must pass observational tests. This includes precision tests in the laboratory and in the solar system (in particular, measurements of the bending of light, the Shapiro effect, perihelion advance, lunar laser ranging, etc.), observations of close binary pulsars (the rate of kinetic energy loss due to gravitational radiation) and cosmological structure formation (CMB temperature fluctuations, large-scale distribution of matter). It is very difficult to construct viable alternatives to Einstein’s theory that do not fail these observational tests.
I found really interesting the theory of Jean Pierre Petit, the Janus model. You can all the info at his web site http://jp-petit.org/. It is in french, but it is not difficult to translate. He basically explains with a single hypothesis the anomalous rotation speed of the galaxies, some important aspects of the large scale structure of the universe, the accelerating expansion of the universe (explained without need of dark matter and energy) and other minor problems (pioneer anomaly could be among them). In the site you can find the relevant math and the reference to published papers with the details of theory. Regards