Yesterday, we posted our latest paper on arXiv. Again, it is a paper about the solar gravitational lens.
This time around, our focus was on imaging an extended object, which of course can be trivially modeled as a multitude of point sources.
However, it is a multitude of point sources at a finite distance from the Sun.
This adds a twist. Previously, we modeled light from sources located at infinity: Incident light was in the form of plane waves.
But when the point source is at a finite distance, light from it comes in the form of spherical waves.
Now it is true that at a very large distance from the source, considering only a narrow beam of light, we can approximate those spherical waves as plane waves (paraxial approximation). But it still leaves us with the altered geometry.
But this is where a second observation becomes significant: As we can intuit, and as it is made evident through the use of the eikonal approximation, most of the time we can restrict our focus onto a single ray of light. A ray that, when deflected by the Sun, defines a plane. And the investigation can proceed in this plane.
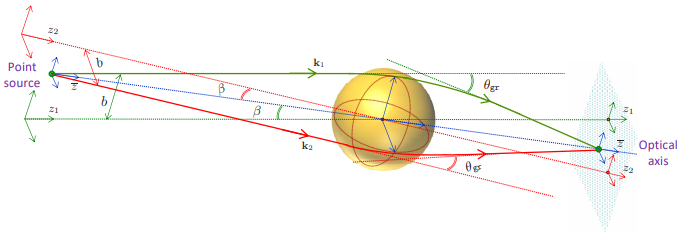
The image above depicts two such planes, corresponding to the red and the green ray of light.
These rays do meet, however, at the axis of symmetry of the problem, which we call the optical axis. However, in the vicinity of this axis the symmetry of the problem is recovered, and the result no longer depends on the azimuthal angle that defines the plane in question.
To make a long story short, this allows us to reuse our previous results, by introducing the additional angle β, which determines, among other things, the additional distance (compared to parallel rays of light coming from infinity) that these light rays travel before meeting at the optical axis.
This is what our latest paper describes, in full detail.