Pioneer Anomaly
\(\renewcommand{\vec}[1]{\boldsymbol{\mathrm{#1}}}\)In 1972, NASA launched its most ambitious space probe to date: Pioneer 10 was designed for the first time to leave the inner solar system, cross the asteroid belt, perform close-up observations of Jupiter, and continue to fly out of the solar system on an hyperbolic escape trajectory. A year later, its sister craft, Pioneer 11 followed on an orbit that took it not just to Jupiter, but also to Saturn several years later.
The Pioneer spacecraft were spin stabilized, requiring very few attitude correction maneuvers to maintain an Earth-pointing orientation of their high gain antenna. The small number of maneuvers means that Pioneer 10 and 11 flew most of the time undisturbed.
Pioneer 10 survived for over 30 years, the last communication taking place in 2003. The life of Pioneer 11 was a little shorter; last communication took place in 1995, but the spacecraft ceased providing precision orbit measurements in 1990, due to a glitch in its radio communication subsystem.
The line-of-sight velocity of the Pioneer spacecraft was measured using radio Doppler observations. During their long operating life, the two Pioneer spacecraft provided a near continuous stream of Doppler data. This allowed precision orbit determination at a level that remains unsurpassed to this date.
When the Pioneer Doppler data set is fitted to models of the known gravitational forces in the solar system, there is a discrepancy. After all known effects (including small nongravitational forces) are accounted for, we find that the discrepancy remains; however, it can be eliminated if we assume the presence of a small, approximately constant, approximately sunward pointing acceleration. The magnitude of this acceleration is very small: about \(10^{-9}~{\rm m}/{\rm s}^2\), which is roughly one ten billionth of the gravitational acceleration on the surface of the Earth. Nevertheless, if this is a real acceleration, it’d mean that by the end of its useful life, Pioneer 10 was nearly half a million kilometers off course.
What can possibly cause this discrepancy? The answer seemed elusive for a long time, although it was always considered strongly likely that the explanation is mundane: heat emitted by the spacecraft preferentially in one direction may be sufficient to cause an acceleration of the required magnitude. Our work to model the thermal behavior of Pioneer 10 and 11 relied, among other things, on a reconstruction of the engineering history of the spacecraft, made possible by recovered telemetry data.
There were, of course, other alternatives: the possibility that Pioneer has detected new physics beyond Einstein right here within the solar system would have been tremendously exciting.
Getting into more detail, first it is important to understand exactly how the Pioneer Doppler observations have been made. The process can be schematically illustrated by this diagram:
The measurement is being made at the receiver, located on the surface of the (spinning, orbiting) Earth (hence the twisted world lines in this schematic). Here, cycles are counted for a set period of time between \(t_1\) and \(t_2\). These two instances of time are projected back onto the spacecraft’s, and eventually, onto the Earth-based transmitter’s world line. (The Pioneer spacecraft had no precision oscillators on board; all precision Doppler measurements were “two-way” or “three-way” measurements, where the spacecraft essentially relayed back a signal that originated on the Earth, either at the same station that received the spacecraft’s signal or at a different station.) The light cones of the radio signals and the spacecraft’s trajectory are calculated by a precision model, which accounts for post-Newtonian gravity, maneuvers, small non-gravitational forces such as propellant leaks and solar pressure, the effects of gravity (Shapiro delay) on the signal, effects of the interplanetary medium (charged solar plasma) and the atmosphere, and the accurate positions of ground stations, taking into account ground tides and continental drift. This model allows us to compute the time interval at the transmitter that corresponds to \(t_1\) and \(t_2\) at the receiver. The transmitter’s frequency is known; thus, we know the number of cycles that were transmitted during this interval. This must agree with the number of cycles received. If it does not, the parameters of the model are modified until a best match is achieved.
Spacecraft orbits can be modeled using the post-Newtonian equations of motion:
\[\frac{d^2\vec{r}}{dt^2}=\frac{\mu_i}{|\vec{r}_i-\vec{r}|^3}\left[A_i(\vec{r}_i-\vec{r})+\vec{B}_i\right],\]
where \(\vec{r}\) is the spacecraft’s position, \(\vec{r}_i\) is the position, \(\mu_i\) is the mass of the \(i\)-th solar system body, \(t\) is the time and the post-Newtonian correction terms \(A_i\) and \(\vec{B}_i\) are given by
\begin{align}A_i&=1-\frac{1}{c^2}\left\{2(\beta+\gamma)\sum\limits_j\frac{\mu_j}{|\vec{r}_j-\vec{r}|}+\gamma v^2+(1+\gamma)v_i^2-2(1+\gamma)\vec{v}\cdot\vec{v}_i-\frac{3}{2}\left[\frac{(\vec{r}-\vec{r}_i)\cdot\vec{v}_i}{|\vec{r}_i-\vec{r}|}\right]^2\right\},\\
\vec{B}_i&=\frac{1}{c^2}\left\{(\vec{r}-\vec{r}_i)\cdot\left[(2+2\gamma)\vec{v}-(1+2\gamma)\vec{v}_i\right]\right\}(\vec{v}-\vec{v}_i).\end{align}
The parameters \(\beta\) and \(\gamma\) are the so-called Eddington-parameters; they are both 1 for general relativity, but may have different values for alternate theories of gravity.
Oblateness of a planetary body modifies its gravitational field. The difference between the actual potential field of an oblate body and a spherically symmetric field can be described using spherical harmonics.
The Pioneer spacecraft had close encounters with Jupiter and (for Pioneer 11 only) Saturn. Both of these planetary bodies are rotationally symmetrical. Their gravitational potential field due to body \(i\) is described by the following equation:
\[U_i=\frac{\mu_i}{|\vec{r}_i-\vec{r}|}\left[1-\sum\limits_k\left(J_ka^k\frac{P_k(\sin\theta)}{|\vec{r}_i-\vec{r}|^k}\right)\right],\]
where \(P_k\) is the \(k\)-th Legendre polynomial, \(a\) is the equatorial radius of the planet, \(\theta\) is the latitude of the spacecraft relative to the planet’s equator, and \(J_k\) are the spherical harmonic coefficients specific to the planet.
In order to put this equation to use, first it must be translated into an expression for force by calculating its gradient. Second, it is also necessary to express the position of the spacecraft in a coordinate system that is fixed to the planet’s center and equator.
In a Cartesian coordinate system with the \(x_1x_2\) plane fixed to the planet’s equator, we have
\begin{align}r&=\sqrt{x_1^2+x_2^2+x_3^2},\\
\theta&=\arctan \frac{x^3}{\sqrt{x_1^2+x_2^2}}.\end{align}
The gradient of the potential field can be expressed as
\[\frac{\partial U_i}{\partial x_j}=\frac{\partial U_i}{\partial r}\frac{\partial r}{\partial x_j}+\frac{\partial U_i}{\partial\theta}\frac{\partial\theta}{\partial x_j}.\]
To use these formulae, the position of the spacecraft must be expressed in a coordinate system that is rotated to coincide with the planet’s equatorial plane. The direction of the planet’s North pole (which is normal to the equatorial plane) is known in the form of its right ascension (\(\alpha\)) and declination (\(\delta\)) angles.
Equations of motion are integrated using Ephemeris Time (ET). Converting from ET to atomic time (TAI) can be accomplished using the following approximate formula:
\[{\rm ET}-{\rm TAI}=32.184+1.657\times 10^{-3}\sin E,\]
where
\begin{align}E&=M+0.01671\sin M,\\
M&=6.239996+1.99096871\times 10^{-7}t,\end{align}
where \(t\) is ET in seconds past J2000.
Doppler data is recorded using UTC timestamps. The difference between UTC and TAI is an integer number of seconds ranging from 10 to 32 as leap seconds were added (UTC is a discontinuous time scale.)
The time delay due to the gravitational field of a body such as the Sun can be calculated using
\[\Delta t=\frac{l}{c}\ln\frac{r_1+r_2+r_{12}+l}{r_1+r_2-r_{12}+l},\]
where \(l=\mu(1+\gamma)/c^2\); \(\mu\) is the mass of the body whose potential field is being considered, multiplied by the gravitational constant; \(\gamma\) is one of the Eddington-parameters (\(\gamma=1\) for general relativity); \(r_1\) and \(r_2\) are the distances of the transmitter and the receiver from the gravitating body, while \(r_{12}\) is the distance between the transmitter and the receiver.
Delay due to solar plasma is a function of the electron density of the plasma. The resulting propagation delay \(\Delta t\) can be approximated using the equation
\[\Delta t=1.3446\times 10^{-25}f^{-2}\int N_e~dl~{\rm s},\]
where \(f\) is the signal frequency and \(N_e\) is the electron density integrated along the propagation path \(l\). For \(N_e\), one particular approximation is in the form
\[N_e\simeq 2.21\times 10^{14}\left(\frac{r}{R_\odot}\right)^{-6}+1.55\times 10^{12}\left(\frac{r}{R_\odot}\right)^{-2.3},\]
where \(R_\odot=6.96\times 10^{8}~{\rm m}\) is the solar radius and \(r\) is the distance from the Sun.
The tropospheric propagation delay (mostly due to moisture in the atmosphere) can be calculated using the formula
\[R=\frac{1}{\sin E+\frac{A}{\tan E+B}},\]
where \(R\) is the additional propagation path, \(E\) is the angle of elevation above the horizon, and the parameters \(A=A_\mathrm{dry}+A_\mathrm{wet}\) and \(B=B_\mathrm{dry}+B_\mathrm{wet}\) can be approximated as
\begin{align}A_\mathrm{dry}&=0.00143,\\
A_\mathrm{wet}&=0.00035,\\
B_\mathrm{dry}&=0.0445,\\
B_\mathrm{wet}&=0.017.\end{align}
Momentum transferred to the spacecraft by intercepted solar photons is described by the equation
\[\vec{F}_\mathrm{intcpt}=\frac{sA(\vec{r}\cdot\vec{n})\vec{r}}{cr^4},\]
where \(s\) is the solar constant (\(s\simeq1.366~{\rm kW}/{\rm m}^2\) at 1 AU), \(A\) is the cross-sectional surface of the spacecraft (\(A\simeq 5.91~{\rm m}^2\) if the HGA is facing the Sun directly), \(\vec{n}\) is a unit vector in the direction of the spacecraft spin axis, and \(\vec{r}\) is the Sun-spacecraft vector. Any additional recoil force due to reflected or absorbed and then reemitted solar radiation can be similarly calculated.
Additionally, maneuvers can be modeled as effectively instantaneous changes in velocity; for high precision modeling, fuel leaks (which inevitably follow maneuvers) can be modeled using a polynomial or exponential decay model.
These calculations should yield a Doppler residual (i.e., the difference between computed and observed cycles per second) no greater than a few mHz. This, however, is not the case for Pioneer 10 and 11; the Doppler residuals are several times larger. However, incorporating a hypothetical Sunward acceleration with a magnitude of
\[a_P=(8.74\pm 1.33)\times 10^{-10}~{\rm m}/{\rm s}^2,\]
reduces the Doppler residuals to an acceptable level. This acceleration of unknown origin is what became known as the Pioneer Anomaly.
More recently, we modeled the thermal recoil force. On Pioneer 10 and 11, we have two main heat sources. First, there is electrical heat: all the instruments on board use about 100 W of electricity, most of which is converted into heat. Second, electricity is produced, very inefficiently, by a set of four radioisotope thermoelectric generators (RTGs); these produce more than 2 kW of waste heat. All this heat has to go somewhere, and most of this heat will be dissipated preferably in one direction, behind the spacecraft’s large dish antenna, which is always pointed towards the Earth. We established that the thermal recoil force is very accurately described as a simple linear combination of heat from two heat sources: electrical heat and heat from the RTGs. The thermal acceleration \(a\) is, in fact
$$a=\frac{1}{mc}(\eta_{\rm rtg}P_{\rm rtg} + \eta_{\rm elec}P_{\rm elec}),$$
where \(c\) is the speed of light, \(m\) is the mass of the spacecraft, \(P_{\rm rtg}\) and \(P_{\rm elec}\) are the RTG and electrical heats, respectively, and \(\eta_{\rm rtg}\) and \(\eta_{\rm elec}\) are “efficiency factors”.
This simple force model is very useful because it can be incorporated directly into the orbital model of the spacecraft. Its validity was confirmed by a very thorough and comprehensive model of the Pioneer spacecraft, using the same software tools (not to mention considerable expertise) that they use for “live” spacecraft. With this model, we were able to predict the thermal recoil force with the greatest accuracy possible, at different points along the trajectory of the spacecraft. The result can be compared directly to the acceleration that is “measured”; i.e., the acceleration that is needed to model the radio signal accurately:
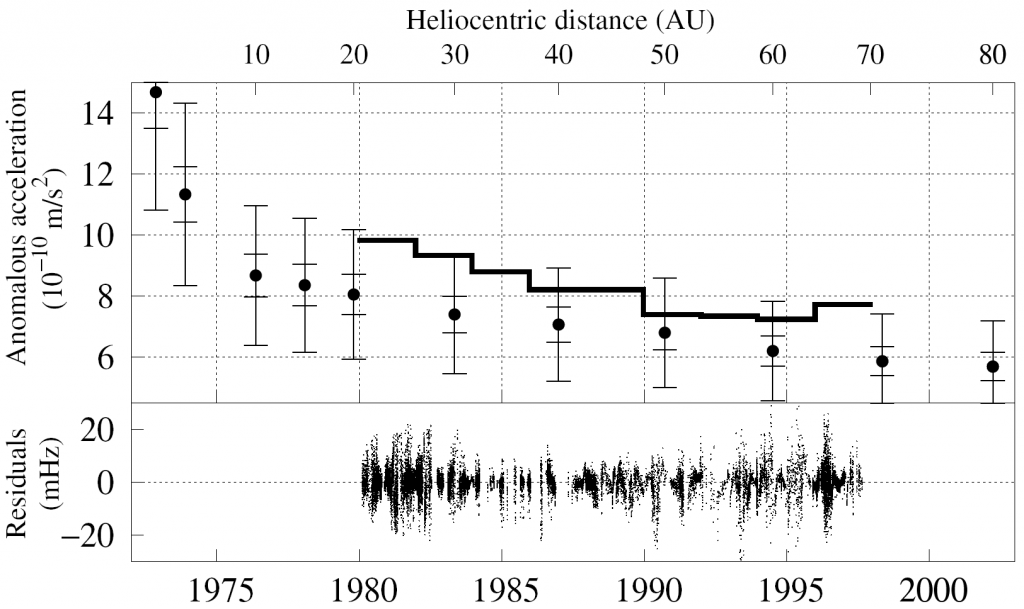
In this plot, the step-function like curve (thick line) is the acceleration deduced from the radio signal frequency. The data points with vertical error bars represent the recoil force calculated from the thermal model. They are rather close. The relatively large error bars are due primarily to the fact that we simply don’t know what happened to the white paint that coated the RTGs. These were hot (the RTGs were sizzling hot even in deep space) and subjected to solar radiation (ultraviolet light and charged particles) so the properties of the paint may have changed significantly over time… we just don’t know how. The lower part of the plot shows just how well the radio signal is modeled; the average residual is less than 5 mHz. The actual frequency of the radio signal is 2 GHz, so this represents a modeling accuracy of less than one part in 100 billion, over the course of nearly 20 years.
In terms of the above-mentioned efficiency factors, the thermal model yielded \(\eta_{\rm rtg}=0.0104\) and \(\eta_{\rm elec}=0.406\).
We also incorporated the thermal recoil force directly into the Doppler analysis that was carried out by Jordan Ellis. Jordan found best-fit residuals at \(\eta_{\rm rtg}=0.0144\) and \(\eta_{\rm elec}=0.480\). These are somewhat larger than the values from the thermal model. But how much larger?
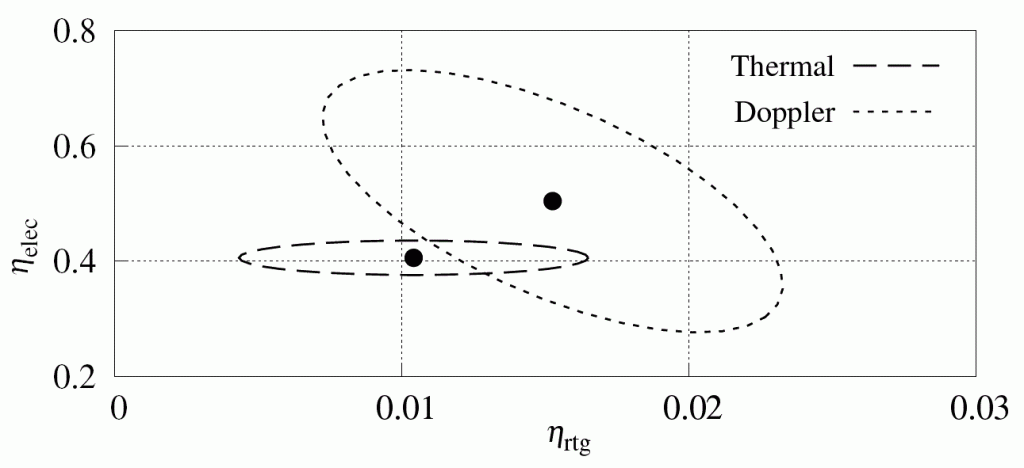
We found that the best way to answer this question was to plot the two results in the parameter space defined by these two efficiency factors:
The dashed ellipse here represents the estimates from the thermal model and their associated uncertainty. The ellipse is elongated horizontally, because the largest source of uncertainty, the degradation of RTG paint, affects only the \(\eta_{\rm rtg}\) factor.
The dotted ellipse represents the estimates from radio signal measurements. The formal error of these estimates is very small (the error ellipse would be invisibly tiny). These formal errors, however, are calculated by assuming that the error in every one of the tends of thousands of Doppler measurements arises independently. In reality, this is not the case: the Doppler measurements are insanely accurate, any errors that occur are a result of systematic mismodeling, e.g., caused by our inadequate knowledge of the solar system. This inflates the error ellipse and that is what was shown in this plot.
The literature of the Pioneer anomaly is huge. Much of it is about attempts to explain the anomaly.First, I’d mention our review article, just published by Living Reviews in Relativity, that provides a thorough overview of the anomaly and summarizes the published research literature to date:
- The Pioneer Anomaly
Slava G. Turyshev and Viktor T. Toth, Living Rev. Relativity 13 (2010), 4.
A comprehensive review paper.
More recently, we published two short papers, dealing with the combined results of our extended Doppler analysis and comprehensive thermal analysis:
- Support for the thermal origin of the Pioneer anomaly
Slava G. Turyshev, Viktor T. Toth, Gary Kinsella, Siu-Chun Lee, Shing M. Lok and Jordan Ellis, Phys. Rev. Lett. 108, 241101 (2012).
Results from a comprehensive thermal model and from Doppler analysis that incorporated the thermal recoil force. - Support for temporally varying behavior of the Pioneer anomaly from the extended Pioneer 10 and 11 Doppler data sets
Slava G. Turyshev, Viktor T. Toth, Jordan Ellis and Craig B. Markwardt, Phys. Rev. Lett. 107, 081103 (2011).
Results from analyzing 20 years of Pioneer 10 and 10 years of Pioneer 11 Doppler data, showing temporal decay.
Other important papers include the original announcement, and reports on the study of the anomaly, including original proposals (by Katz, Murphy and later, Scheffer) concerning the thermal origin:
- Indication, from Pioneer 10/11, Galileo, and Ulysses Data, of an Apparent Anomalous, Weak, Long-Range Acceleration.
J. D. Anderson and P. A. Laing and E. L. Lau and A. S. Liu and M. M. Nieto S. G. Turyshev. Physical Review Letters, Vol 81, No 14, 2858-2861 (1998).
This is the original paper reporting on the discovery of the anomalous acceleration. - Comment on “Indication, from Pioneer 10/11, Galileo, and Ulysses Data, of an Apparent Anomalous, Weak, Long-Range Acceleration”.
J. I. Katz. Physical Review Letters, Vol 83, No 9, 1892 (1999).
One of two replies raising the possibility that the anomaly may be due to prosaic causes. - A Prosaic Explanation for the Anomalous Acceleration Seen in Distant Spacecraft.
Edward M. Murphy. Physical Review Letters, Vol 83, No 9, 1890 (1999).
The second of two replies raising the possibility that the anomaly has a prosaic cause. - Reply (to the comment by Katz on “Indication, from Pioneer 10/11, Galileo, and Ulysses Data, of an Apparent Anomalous, Weak, Long-Range Acceleration”).
J. D. Anderson and P. A. Laing and E. L. Lau and A. S. Liu and M. M. Nieto S. G. Turyshev. Physical Review Letters, Vol 83, No 9, 1893 (1999).
Anderson and collaborators dispute the possibility that anisotropic heat radiation was sufficient to cause the anomaly. - Reply (to the comment by Murphy on “Indication, from Pioneer 10/11, Galileo, and Ulysses Data, of an Apparent Anomalous, Weak, Long-Range Acceleration”).
J. D. Anderson and P. A. Laing and E. L. Lau and A. S. Liu and M. M. Nieto S. G. Turyshev. Physical Review Letters, Vol 83, No 9, 1891 (1999).
Anderson and collaborators dispute the possibility that electrical heat can be responsible for the anomalous acceleration. - Conventional Forces can Explain the Anomalous Acceleration of Pioneer 10.
L. K. Scheffer. Physical Review D, Vol 67, No 8, 084021 (2003).
A detailed study by Lou Scheffer of the conventional forces present on Pioneer 10, which seem to be sufficient to account for the anomalous acceleration. - Study of the anomalous acceleration of Pioneer 10 and 11.
J. D. Anderson and P. A. Laing and E. L. Lau and A. S. Liu and M. M. Nieto and S. G. Turyshev. Physical Review D, Vol 65, No 8, 082004 (2004).
This is the “big paper”, the most comprehensive study to date of the Pioneer anomaly. - Independent Confirmation of the Pioneer 10 Anomalous Acceleration.
Craig B. Markwardt. eprint arXiv:gr-qc/0208046.
The first of several truly independent confirmations that the anomaly is indeed present in the Pioneer Doppler data. - A study of the Pioneer anomaly: New data and objectives for new investigation.
S. G. Turyshev and V. T. Toth and L. R. Kellogg and E. L. Lau and K. J. Lee. IJMPD Vol 15, No 1, 1-55 (2006).
The first detailed account of newly recovered Doppler and telemetry data. - The Pioneer anomaly: seeking an explanation in newly recovered data.
V. T. Toth and S. G. Turyshev. Can. J. Phys. 84: 1063-1087 (2006).
Further details about the new data, mostly focusing on the telemetry. - The constancy of the Pioneer anomalous acceleration.
Ø. Olsen. A&A 463, 393-397 (2007).
Another independent confirmation of the Pioneer acceleration, with emphasis on studying its constancy. - Pioneer Anomaly: Evaluating Newly Recovered Data.
V. T. Toth and S. G. Turyshev. AIP Conference Proceedings, Volume 977, pp. 264-283 (2008).
Further details about the on-going study of the anomaly, including thermal models under development. - Independent analysis of the orbits of Pioneer 10 and 11.
Viktor. T. Toth. IJMPD Vol 18, No 5, 717-741 (2009).
Independently developed orbit determination code confirming the Pioneer anomaly and showing the presence of a possible jerk term in the data. - Thermal recoil force, telemetry, and the Pioneer anomaly.
Viktor. T. Toth and Slava G. Turyshev. , Phys. Rev. D. 79, 043011 (2009)
The formalism of the thermal recoil force as a function of telemetry and its applicability to Pioneer, shown using a simulated data set.

[…] paper about the thermal analysis of Pioneer 10 and 11 was accepted for publication by Physical Review and it is now on […]
[…] The Pioneer Anomaly […]
[…] Pioneer Anomaly […]