July 2021 – Spinor Info

The book of 1000 wonders

Jul 302021

On my eighth birthday, I received a gift from a nice couple, friends of my Mom.

It was a Hungarian-language book bearing the title, “Wonders of the World,” in Hungarian, translated from the German original that was written by German-Jewish authors Artur Fürst and Alexander Moszkowski.

It was an old book, published in the 1930s. A dark green hardcover, with the etched image of a skyscraper for illustration on the cover. Its dust jacket, if it ever had one, was long gone.

But never mind that, it’s the content on these yellowed pages that matters.

It was from this book that I first learned about statistical fallacies, for instance. What is the probability that when you leave your home, the first 200 people you encounter are all males? Astronomically small, you might conclude. 2⁻²⁰⁰ ~ 6.223 × 10⁻⁶¹ to be a bit more precise, assuming half the population is male. A probability this small is firmly in the category of never happens. Until one morning, you step outside and the first thing you see is an all-male battalion of soldiers marching down the street…

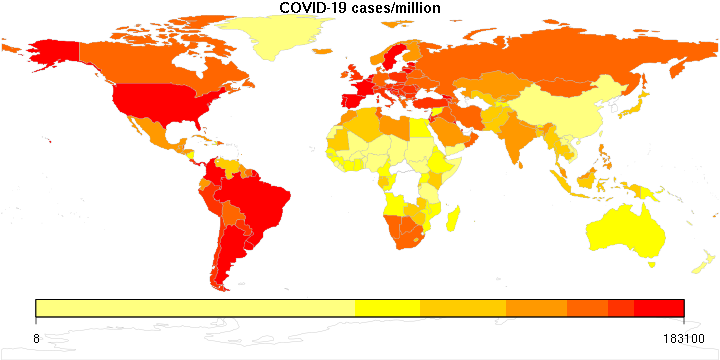
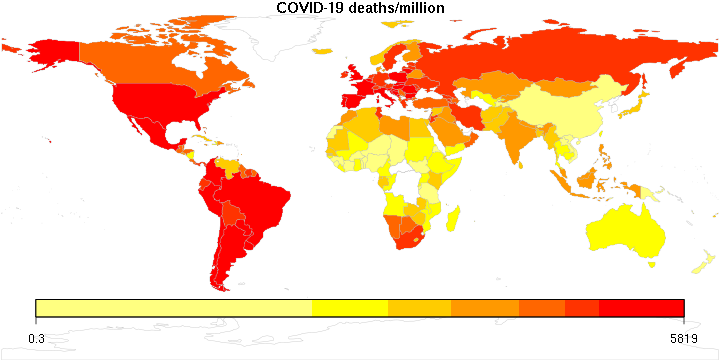
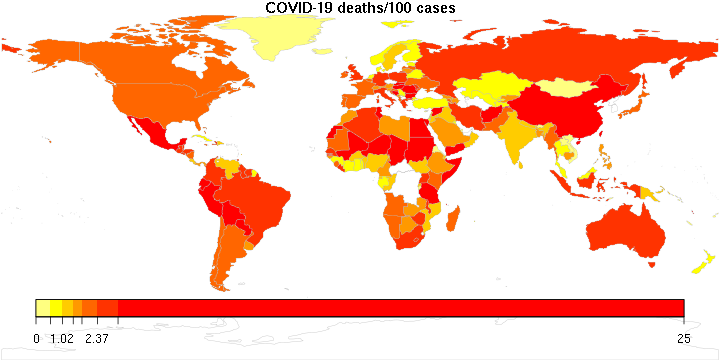
I was reminded of this book today as I was reading about recent pronouncements of “breakthrough” infections among the vaccinated, and the reminder by experts that in a population that has a high vaccination rate, such cases are to be expected. It does not mean that the vaccine is worthless. It simply means that as the virus runs out of unvaccinated victims, to the extent it can still cause damage, increasingly it will be among the vaccinated folks. Which should make sense, except, as we well know, roughly 90% of statistical fallacies are committed by right-handed people…

Anyhow, much to my surprise, this book I love so much, from which I learned so much as a pre-teen, remains well-known in the country where it was originally published under the title Das Buch der 1000 Wunder. So well-known, in fact, that current German-language editions are readily available on Amazon, nearly a century after its initial publication. So I guess I am not the only person who finds the insights and information presented in this unassuming volume immensely valuable, especially for a child.

So let this serve as my notice of gratitude across time and space to “uncle Sandor and aunt Eva,” as they inscribed their names in the book along with their birthday wishes, for what I can now truly call a gift of a lifetime.

Steven Weinberg

Physics No Responses »

Jul 242021

Can you guess the author with the most physics books on what I call my “primary” bookshelf, the shelf right over my desk where I keep the books that I use the most often?

It would be Steven Weinberg. His 1972 Gravitation and Cosmology remains one of the best books ever on relativity theory, working out details in ways no other book does. His 2010 Cosmology remains a reasonably up-to-date textbook on modern cosmology. And then there is of course the 3-volume Quantum Theory of Fields.

Alas, Weinberg is no longer with us. He passed away yesterday, July 23, at the age of 88.

He will be missed.

Ghost in the machine

Cybernetics 1 Response »

Jul 232021

I just came across an account describing an AI chatbot that I found deeply disturbing.

You see… the chatbot turned out to be a simulation of a young woman, someone’s girlfriend, who passed away years ago at a tragically young age, while waiting for a liver transplant.

Except that she came back to live, in a manner of speaking, as the disembodied personality of an AI chatbot.

Yes, this is an old science-fiction trope. Except that it is not science-fiction anymore. This is our real world, here in the year 2021.

When I say I find the story deeply disturbing, I don’t necessarily mean it disapprovingly. AI is, after all, the future. For all I know, in the distant future AI may be the only way our civilization will survive, long after flesh-and-blood humans are gone.

Even so, this story raises so many questions. The impact on the grieving. The rights of the deceased. And last but not least, at what point does AI become more than just a clever algorithm that can string words together? At what time do we have to begin to worry about the rights of the thinking machines we create?

Hello, all. Welcome to the future.

Visegrád

History, Hungary, Personal No Responses »

Jul 152021

I wrote an answer today on Quora that, I realized, belongs in my blog.

The question was about once significant medieval towns in Europe that have since faded into obscurity.

And I had the perfect answer, on account of having lived there back in the 1970s: The town of Visegrád in northern Hungary (known these days on account of the Visegrad Four, the informal alliance of the Czech Republic, Hungary, Poland and Slovakia which began with a summit in this town held in 1991).

Once the capital of the Kingdom of Hungary, and also home of the Summer Palace of King Matthias Corvinus during the heyday of said kingdom, today the town (really, a village; it gained the legal status of town only because of its historical significance, not on account of its population, which numbers less than 2,000) is just a minor settlement at the Danube Bend, where where the river Danube makes a 90-degree turn towards Budapest.

I used to live in a building just at the base of the stocky Salamon tower near the center of this image. Image from Wikipedia.

Visegrád is a fascinating town, full of history. Unfortunately, because of said history, most of it is in the form of barely recognizable ruins. Ruins of a citadel at the top of Castle Hill, its last functioning remains blown up by the victorious Austrians after the failed struggle for Hungarian independence in the early 18th century. Ruins of the sprawling Summer Palace complex, used by locals as a source of building material for centuries until very little of the original buildings remained. Ruins of the tower of Salamon, part of the lower castle, rebuilt decades ago using modern materials and housing a museum, but badly in need of repairs. And more ruins, ruins going back to Roman times, everywhere.

The name of the town itself is of Slavic origin (literally means high castle I believe) but many of the town’s present-day inhabitants are of German descent. I recall names of classmates like Gerstmayer or Fröhlich, and it was not uncommon to hear family members talking to each other in German on the streets of the town when I lived there as a child.

I have fond memories of the place; I attended school there from grades 6 to 8 before moving back to Budapest. I still visit Visegrád from time to time when I am in Hungary, albeit only as a tourist, as I no longer really know anybody there. It is, to be sure, a very popular tourist destination: the Danube Bend is spectacular, and the hills surrounding the area are crisscrossed by well-marked, well-maintained tourist trails. And, well, ruins or no ruins, the history of the place is absolutely fascinating.

But looking at the tiny village, its single church, small school, its sole tiny movie theatre, the few narrow streets with mostly single-story buildings, you’d never guess the rich history of the town.

Church of St. John the Baptist, in the center of Visegrád. Lovely clock. Google Street View image.

Tensor algebra

Computer Algebra No Responses »

Jul 142021

The other day, someone asked a question: Can the itensor package in Maxima calculate the Laplace-Beltrami operator applied to a scalar field in the presence of torsion?

Well, it can. But I was very happy to get this question because it allowed me to uncover some long-standing, subtle bugs in the package that prevented some essential simplifications and in some cases, even produced nonsensical results.

With these fixes, Maxima now produces a beautiful result, as evidenced by this nice newly created demo, which I am about to add to the package:

(%i1) if get('itensor,'version) = false then load(itensor)
(%i2) "First, we set up the basic properties of the system"
(%i3) imetric(g)
(%i4) "Demo is faster in 3D but works for other values of dim, too" 
(%i5) dim:3
(%i6) "We declare symmetries of the metric and other symbols"
(%i7) decsym(g,2,0,[sym(all)],[])
(%i8) decsym(g,0,2,[],[sym(all)])
(%i9) components(g([a],[b]),kdelta([a],[b]))
(%i10) decsym(levi_civita,0,dim,[],[anti(all)])
(%i11) decsym(itr,2,1,[anti(all)],[])
(%i12) "It is useful to set icounter to avoid indexing conflicts"
(%i13) icounter:100
(%i14) "We choose the appropriate convention for exterior algebra"
(%i15) igeowedge_flag:true
(%i16) "Now let us calculate the Laplacian of a scalar field and simplify"
(%i17) canform(hodge(extdiff(hodge(extdiff(f([],[]))))))
(%i18) contract(expand(lc2kdt(%)))
(%i19) ev(%,kdelta)
(%i20) D1:ishow(canform(%))
                  %1 %2  %3 %4                 %1 %2            %1 %2
(%t20)   (- f    g      g      g     ) + f    g      + f       g
             ,%4  ,%3           %1 %2     ,%2  ,%1      ,%1 %2
(%i21) "We can re-express the result using Christoffel symbols, too"
(%i22) ishow(canform(conmetderiv(D1,g)))
               %1 %4  %2 %5      %3                   %1 %2      %3
(%t22) 2 f    g      g      ichr2      g      - f    g      ichr2
          ,%5                    %1 %2  %3 %4    ,%3             %1 %2
                                              %1 %3      %2               %1 %2
                                      - f    g      ichr2      + f       g
                                         ,%3             %1 %2    ,%1 %2
(%i23) "Nice. Now let us repeat the same calculation with torsion"
(%i24) itorsion_flag:true
(%i25) canform(hodge(extdiff(hodge(extdiff(f([],[]))))))
(%i26) "Additional simplifications are now needed"
(%i27) contract(expand(lc2kdt(%th(2))))
(%i28) ev(%,kdelta)
(%i29) canform(%)
(%i30) ev(%,ichr2)
(%i31) ev(%,ikt2)
(%i32) ev(%,ikt1)
(%i33) ev(%,g)
(%i34) ev(%,ichr1)
(%i35) contract(rename(expand(canform(%))))
(%i36) flipflag:not flipflag
(%i37) D2:ishow(canform(%th(2)))
                %1 %2  %3 %4                 %1 %2    %3            %1 %2
(%t37) (- f    g      g      g     ) + f    g      itr      + f    g
           ,%1         ,%2    %3 %4     ,%1           %2 %3    ,%1  ,%2
                                                                          %1 %2
                                                               + f       g
                                                                  ,%1 %2
(%i38) "Another clean result; can also be expressed using Christoffel symbols"
(%i39) ishow(canform(conmetderiv(D2,g)))
               %1 %2  %3 %4      %5                   %1 %2    %3
(%t39) 2 f    g      g      ichr2      g      + f    g      itr
          ,%1                    %2 %3  %4 %5    ,%1           %2 %3
                     %1 %2      %3            %2 %3      %1               %1 %2
             - f    g      ichr2      - f    g      ichr2      + f       g
                ,%1             %2 %3    ,%1             %2 %3    ,%1 %2
(%i40) "Finally, we see that the two results differ only by torsion"
(%i41) ishow(canform(D2-D1))
                                   %1 %2    %3
(%t41)                       f    g      itr
                              ,%1           %2 %3
(%i42) "Last but not least, d^2 is not nilpotent in the presence of torsion"
(%i43) extdiff(extdiff(f([],[])))
(%i44) ev(%,icc2,ikt2,ikt1)
(%i45) canform(%)
(%i46) ev(%,g)
(%i47) ishow(contract(%))
                                       %3
(%t47)                         f    itr
                                ,%3    %275 %277
(%i48) "Reminder: when dim = 2n, the Laplacian is -1 times these results."

The learning curve is steep and there are many pitfalls, but itensor remains an immensely powerful package.

Updated COVID maps

Health No Responses »

Jul 142021

I was looking for something else in my blog when I came across this post of mine from last May, putting my rusty R programming skills to use and producing some maps representing COVID-19 statistics.

Needless to say, the situation is quite different today, but in some ways at least, the more things change the more they remain the same.

The number of cases per million people is up, way up of course.

However, the trend remains the same: the worst numbers come from Europe and the Americas. I still cannot decide if this is a characteristic of COVID-19 or simply a result of more thorough testing and more transparent reporting in liberal democracies.

The death statistic is also similar:

The reddest areas are again the Americas and Europe, including Russia, but also Iran. The encouraging news is that the death rate per million didn’t rise quite as fast as the number of cases per million population. This may indicate that we have become more successful treating people (of course a more sinister possibility is that the most vulnerable, such as the elderly in homes, died first, pushing up last year’s death statistic.)

To see this more clearly, here is the mortality rate, that is, the percentage of deaths per cases:

Last year, North America and Europe, along with China, led the pack. This year, it’s quite different: both North America and Western Europe have fallen behind, which is to say, fewer people who catch COVID-19 actually die.

Another difference of course is that we can now protect ourselves and others around us by getting vaccinated. So please, do not hesitate, do not buy into insane conspiracy theories. Vaccines carry a tiny risk, but so does stepping outside to do your shopping, because you never know when a wayward car might jump the curb and kill you. But vaccines also protect you from a debilitating illness that often cripples even its survivors with lasting health effects. And no, vaccines are not an evil plot by Gates or Soros to get you microchipped; the technology just doesn’t work that way. Similarly, no, 5G cellular technology, which is mostly about using radio waves more efficiently, often with less power than current networks, has nothing to do with biology. Last but not least, whether the virus came from bats or a lab (there is little doubt in the literature that it is of natural origin, but that does not exclude the possibility that it was released from a lab by accident — such accidents are known to have happened even in high biosafety labs around the world) makes no difference: in the end, it can kill or maim you just the same, and the best way to protect yourself and your loved ones is through vaccination and responsible behavior (masks, distancing). In short (and with apologies for preaching): it’s not politics, people. It’s epidemiology.