Just completed the release of Maxima 5.49.
I hope I did not mess anything up. Building and releasing a new version is always a bit stressful.
Just a maintenance release but still: I completed the process to release Maxima 5.48.1.
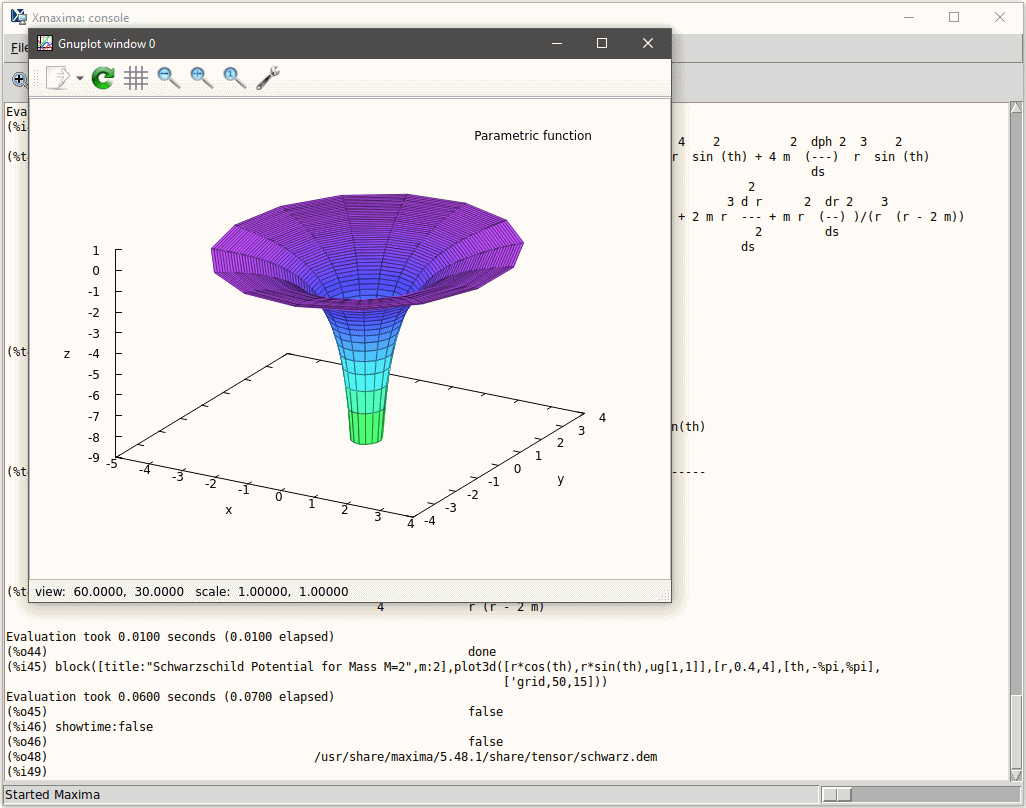
Hope it will serve the community well. I know I’ll be using it a lot.
I just completed the process to release Maxima 5.48.
The new version introduces several noteworthy enhancements for symbolic computation, with improvements in performance, functionality, and user experience.
Highlights:
– Unicode-enabled output (when supported by the Lisp compiler)
– Numerous performance improvements across core routines
– New package for symbolic radical denesting
– New package for inferring closed-form expressions from sequences
– New package for simplification of gamma functions
– Resolution of more than 150 tickets, spanning both long-standing and recent bugs
Developed in Common Lisp, Maxima remains a reliable and customizable tool for research, education, science, and engineering.
To install, explore, or contribute: https://maxima.sourceforge.io
I just finished uploading the latest release, 5.47.0, of our beautiful Maxima project.
It was a harder battle than I anticipated, lots of little build issues I had to fix before it was ready to go.
Maxima remains one of the three major computer algebra systems. Perhaps a bit (but only a bit!) less elegant-looking than Mathematica, and perhaps a bit (but only a bit!) less capable on some friends (exotic integrals, differential equations) than Maple, yet significantly more capable on other fronts (especially I believe abstract index tensor algebra and calculus), it also has a unique property: it’s free and open source.
It is also one of the oldest pieces of major software that remains in continuous use. Its roots go back to the 1960s. I occasionally edit 50-year old code in its LISP code base.
And it works. I use it every day. It is “finger memory”, my “go to” calculator, and of course there’s that tensor algebra bit.
Maxima also has a beautiful graphical interface, which I admit I don’t use much though. You might say that I am “old school” given my preference for the text UI, but that’s really not it: the main reason is that once you know what you’re doing, the text UI is simply more efficient.
I hope folks will welcome this latest release.
We all know that GPT is very competent, very knowledgeable. So let me go ahead and ask a technical question. It’s not trivial but not terribly complicated either; any student studying general relativity should be able to show the correct derivation. Here is my question:
Derive the geodesic equations for \(d\tau^2=Bdt^2-Adr^2-r^2d\theta^2-r^2\sin^2\theta d\phi^2\), where \(A\) and \(B\) are functions of \(r\) only.
Let’s see how GPT3.5 responds:
The geodesic equations for the given metric are given by:
$$\frac{d^2x^\alpha}{d\tau^2}+\Gamma^\alpha_{\mu\nu}\frac{dx^\mu}{d\tau}\frac{dx^\nu}{d\tau}=0$$
where \(\tau\) is the proper time, \(x^\alpha\) are the coordinates \((t,r,\theta,\phi)\), and \(\Gamma^\alpha_{\mu\nu}\) are the Christoffel symbols of the second kind, given by:
$$\Gamma^\alpha_{\mu\nu}=\frac{1}{2}g^{\alpha\beta}(\partial_\mu g_{\beta\nu}+\partial_\nu g_{\beta\mu}-\partial_\beta g_{\mu\nu})$$
where \(g_{\alpha\beta}\) is the metric tensor.
For the given metric, the non-zero Christoffel symbols are:
\begin{align*}
\Gamma^t_{rr}&=\frac{1}{2}B’\\
\Gamma^t_{tt}&=\frac{1}{2}B\frac{A’}{B}\\
\Gamma^r_{rt}&=\frac{1}{2}\frac{A’}{B}\\
\Gamma^r_{rr}&=-\frac{1}{2}\frac{A’}{B}\\
\Gamma^\theta_{r\theta}&=\frac{1}{r}\\
\Gamma^\theta_{\theta\phi}&=-\sin\theta\cos\theta\\
\Gamma^\phi_{r\phi}&=\frac{1}{r}\\
\Gamma^\phi_{\theta\phi}&=\cot\theta
\end{align*}where a prime denotes differentiation with respect to \(r\).
Using these, we can write down the geodesic equations explicitly:
\begin{align*}
\frac{d^2t}{d\tau^2}+\frac{B’}{2B}\left(\frac{dt}{d\tau}\right)^2+\frac{A’}{2B}\left(\frac{dr}{d\tau}\right)\left(\frac{dt}{d\tau}\right)&=0\\
\frac{d^2r}{d\tau^2}-\frac{A’}{2B}\left(\frac{dt}{d\tau}\right)^2+\frac{A’}{2B}\left(\frac{dr}{d\tau}\right)^2+r\left(\left(\frac{d\theta}{d\tau}\right)^2+\sin^2\theta\left(\frac{d\phi}{d\tau}\right)^2\right)&=0\\
\frac{d^2\theta}{d\tau^2}+2\frac{dr}{d\tau}\frac{d\theta}{d\tau}-\sin\theta\cos\theta\left(\frac{d\phi}{d\tau}\right)^2&=0\\
\frac{d^2\phi}{d\tau^2}+2\frac{dr}{d\tau}\frac{d\phi}{d\tau}+2\cot\theta\frac{d\theta}{d\tau}\frac{d\phi}{d\tau}&=0
\end{align*}
Hmmm… sounds eminently knowledgeable, does it not?
Well… maybe not. How about we ask an actual computer algebra system:
(%i1) load(ctensor)$
(%i2) derivabbrev:true$
(%i3) ct_coords:[t,r,u,v]$
(%i4) depends([A,B],[r])$
(%i5) lg:matrix([B,0,0,0],[0,-A,0,0],[0,0,-r^2,0],[0,0,0,-r^2*sin(u)^2])$
(%i6) cmetric(false)$
(%i7) christof(mcs)$
B
r
(%t7) mcs = ---
1, 1, 2 2 A
B
r
(%t8) mcs = ---
1, 2, 1 2 B
A
r
(%t9) mcs = ---
2, 2, 2 2 A
1
(%t10) mcs = -
2, 3, 3 r
1
(%t11) mcs = -
2, 4, 4 r
r
(%t12) mcs = - -
3, 3, 2 A
cos(u)
(%t13) mcs = ------
3, 4, 4 sin(u)
2
r sin (u)
(%t14) mcs = - ---------
4, 4, 2 A
(%t15) mcs = - cos(u) sin(u)
4, 4, 3
(%i16) geod:[0,0,0,0]$
(%i17) cgeodesic(true)$
B t + B r t
s s r s s
(%t17) geod = -----------------
1 B
2 2 2 2 2
2 r sin (u) (v ) + 2 r (u ) - B (t ) - 2 A r - A (r )
s s r s s s r s
(%t18) geod = - --------------------------------------------------------------
2 2 A
2
r cos(u) sin(u) (v ) - r u - 2 r u
s s s s s
(%t19) geod = - ----------------------------------------
3 r
r sin(u) v + 2 r cos(u) u v + 2 r sin(u) v
s s s s s s
(%t20) geod = -------------------------------------------------
4 r sin(u)
Looks different, doesn’t it. And no, I don’t mean LaTeX vs. the fixed pitch character representations of equations in a text terminal. Rather, the content.
The thing is, what GPT produces looks plausible. It has the right idea. The equations seem to make sense. Unless you know what to expect, you are likely to accept the result as correct, since it appears correct. But GPT sucks at math. It gets easily confused. It is a text model that is optimized to write equations that look right… but only has a superficial understanding of what it produces. Kind of like a student who is trying hard to remember, produces something that resembles the right thing, but without a perfect memory (and keep in mind, trained neural nets are not like any other software we are used to using, as they have no perfect memory!) and without in-depth understanding, fails.
I am sure over time this will improve. GPT-4 is already better at it than 3.5 (which was used to produce this outcome). And future versions may likely interface with computer algebra subsystems (among other things) to augment the neural net with specific capabilities. But for now, perhaps I can be forgiven for asking GPT’s cousin, DALL-E, to draw me a cat, exasperated by the bad math GPT produces:

Came across a question tonight: How do you construct the matrix
$$\begin{pmatrix}1&2&…&n\\n&1&…&n-1\\…\\2&3&…&1\end{pmatrix}?$$
Here’s a bit of Maxima code to make it happen:
(%i1) M(n):=apply(matrix,makelist(makelist(mod(x-k+n,n)+1,x,0,n-1),k,0,n-1))$
(%i2) M(5);
[ 1 2 3 4 5 ]
[ ]
[ 5 1 2 3 4 ]
[ ]
(%o2) [ 4 5 1 2 3 ]
[ ]
[ 3 4 5 1 2 ]
[ ]
[ 2 3 4 5 1 ]
I also ended up wondering about the determinants of these matrices:
(%i3) makelist(determinant(M(i)),i,1,10); (%o3) [1, - 3, 18, - 160, 1875, - 27216, 470596, - 9437184, 215233605, - 5500000000]
I became curious if this sequence of numbers was known, and indeed that is the case. It is sequence number A052182 in the Encyclopedia of Integer Sequences: “Determinant of n X n matrix whose rows are cyclic permutations of 1..n.” D’oh.
As it turns out, this sequence also has another name: it’s the Smarandache cyclic determinant sequence. In closed form, it is given by
$${\rm SCDNS}(n)=(-1)^{n+1}\frac{n+1}{2}n^{n-1}.$$
(%i4) SCDNS(n):=(-1)^(n+1)*(n+1)/2*n^(n-1);
n + 1
(- 1) (n + 1) n - 1
(%o4) SCDNS(n) := (------------------) n
2
(%i5) makelist(determinant(SCDNS(i)),i,1,10);
(%o5) [1, - 3, 18, - 160, 1875, - 27216, 470596, - 9437184, 215233605, - 5500000000]
Surprisingly, apart from the alternating sign it shares the first several values with another sequence, A212599. But then they deviate.
Don’t let anyone tell you that math is not fun.
Acting as “release manager” for Maxima, the open-source computer algebra system, I am happy to announce that just minutes ago, I released version 5.46.
I am an avid Maxima user myself; I’ve used Maxima’s tensor algebra packages, in particular, extensively in the context of general relativity and modified gravity. I believe Maxima’s tensor algebra capabilities remain top notch, perhaps even unsurpassed. (What other CAS can derive Einstein’s field equations from the Einstein-Hilbert Lagrangian?)
The Maxima system has more than half a century of history: its roots go back to the 1960s, when I was still in kindergarten. I have been contributing to the project for nearly 20 years myself.
Anyhow, Maxima 5.46, here we go! I hope I made no blunders while preparing this release, but if I did, I’m sure I’ll hear about it shortly.
The other day, someone asked a question: Can the itensor package in Maxima calculate the Laplace-Beltrami operator applied to a scalar field in the presence of torsion?
Well, it can. But I was very happy to get this question because it allowed me to uncover some long-standing, subtle bugs in the package that prevented some essential simplifications and in some cases, even produced nonsensical results.
With these fixes, Maxima now produces a beautiful result, as evidenced by this nice newly created demo, which I am about to add to the package:
(%i1) if get('itensor,'version) = false then load(itensor) (%i2) "First, we set up the basic properties of the system" (%i3) imetric(g) (%i4) "Demo is faster in 3D but works for other values of dim, too" (%i5) dim:3 (%i6) "We declare symmetries of the metric and other symbols" (%i7) decsym(g,2,0,[sym(all)],[]) (%i8) decsym(g,0,2,[],[sym(all)]) (%i9) components(g([a],[b]),kdelta([a],[b])) (%i10) decsym(levi_civita,0,dim,[],[anti(all)]) (%i11) decsym(itr,2,1,[anti(all)],[]) (%i12) "It is useful to set icounter to avoid indexing conflicts" (%i13) icounter:100 (%i14) "We choose the appropriate convention for exterior algebra" (%i15) igeowedge_flag:true (%i16) "Now let us calculate the Laplacian of a scalar field and simplify" (%i17) canform(hodge(extdiff(hodge(extdiff(f([],[])))))) (%i18) contract(expand(lc2kdt(%))) (%i19) ev(%,kdelta) (%i20) D1:ishow(canform(%)) %1 %2 %3 %4 %1 %2 %1 %2 (%t20) (- f g g g ) + f g + f g ,%4 ,%3 %1 %2 ,%2 ,%1 ,%1 %2 (%i21) "We can re-express the result using Christoffel symbols, too" (%i22) ishow(canform(conmetderiv(D1,g))) %1 %4 %2 %5 %3 %1 %2 %3 (%t22) 2 f g g ichr2 g - f g ichr2 ,%5 %1 %2 %3 %4 ,%3 %1 %2 %1 %3 %2 %1 %2 - f g ichr2 + f g ,%3 %1 %2 ,%1 %2 (%i23) "Nice. Now let us repeat the same calculation with torsion" (%i24) itorsion_flag:true (%i25) canform(hodge(extdiff(hodge(extdiff(f([],[])))))) (%i26) "Additional simplifications are now needed" (%i27) contract(expand(lc2kdt(%th(2)))) (%i28) ev(%,kdelta) (%i29) canform(%) (%i30) ev(%,ichr2) (%i31) ev(%,ikt2) (%i32) ev(%,ikt1) (%i33) ev(%,g) (%i34) ev(%,ichr1) (%i35) contract(rename(expand(canform(%)))) (%i36) flipflag:not flipflag (%i37) D2:ishow(canform(%th(2))) %1 %2 %3 %4 %1 %2 %3 %1 %2 (%t37) (- f g g g ) + f g itr + f g ,%1 ,%2 %3 %4 ,%1 %2 %3 ,%1 ,%2 %1 %2 + f g ,%1 %2 (%i38) "Another clean result; can also be expressed using Christoffel symbols" (%i39) ishow(canform(conmetderiv(D2,g))) %1 %2 %3 %4 %5 %1 %2 %3 (%t39) 2 f g g ichr2 g + f g itr ,%1 %2 %3 %4 %5 ,%1 %2 %3 %1 %2 %3 %2 %3 %1 %1 %2 - f g ichr2 - f g ichr2 + f g ,%1 %2 %3 ,%1 %2 %3 ,%1 %2 (%i40) "Finally, we see that the two results differ only by torsion" (%i41) ishow(canform(D2-D1)) %1 %2 %3 (%t41) f g itr ,%1 %2 %3 (%i42) "Last but not least, d^2 is not nilpotent in the presence of torsion" (%i43) extdiff(extdiff(f([],[]))) (%i44) ev(%,icc2,ikt2,ikt1) (%i45) canform(%) (%i46) ev(%,g) (%i47) ishow(contract(%)) %3 (%t47) f itr ,%3 %275 %277 (%i48) "Reminder: when dim = 2n, the Laplacian is -1 times these results."
The learning curve is steep and there are many pitfalls, but itensor remains an immensely powerful package.
We just released another beautiful new version of Maxima, 5.45.0. This time around, it also includes changes (for the first time in years) to the tensor packages, based on a very comprehensive set of proposed patches by a devoted Maxima user.
I am one of the maintainers of the Maxima computer algebra system. Maxima’s origins date back to the 1960s, when I was still in kindergarten. I feel very privileged that I can participate in the continuing development of one of the oldest continuously maintained software system in wide use.
It has been a while since I last dug deep into the core of the Maxima system. My LISP skills are admittedly a bit rusty. But a recent change to a core Maxima capability, its ability to create Taylor-series expansions of expressions, broke an important feature of Maxima’s tensor algebra packages, so it needed fixing.
The fix doesn’t amount to much, just a few lines of code:
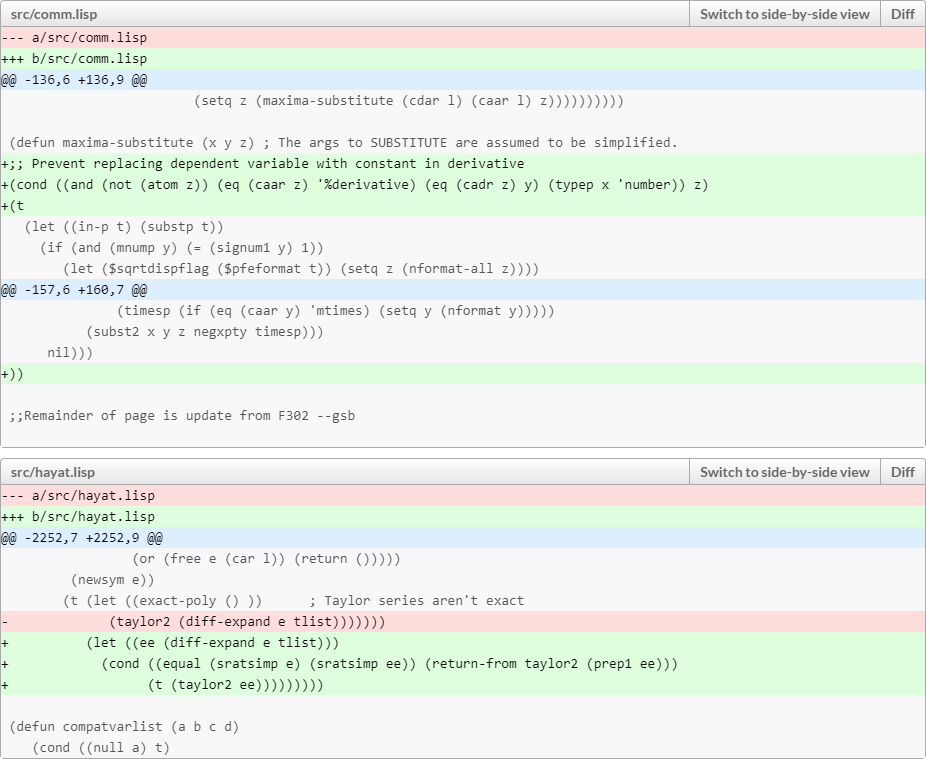
It did take more than a few minutes though to find the right (I hope) way to implement this fix.
Even so, I had fun. This is the kind of programming that I really, really enjoy doing. Sadly, it’s not the kind of programming for which people usually pay you Big Bucks… Oh well. The fun alone was worth it.
And before I forget: Last week, wearing my release manager hat I successfully created a new version of Maxima, the open-source computer algebra system. As a result, Maxima is again named one of SourceForge’s projects of the week, for the week of June 10.
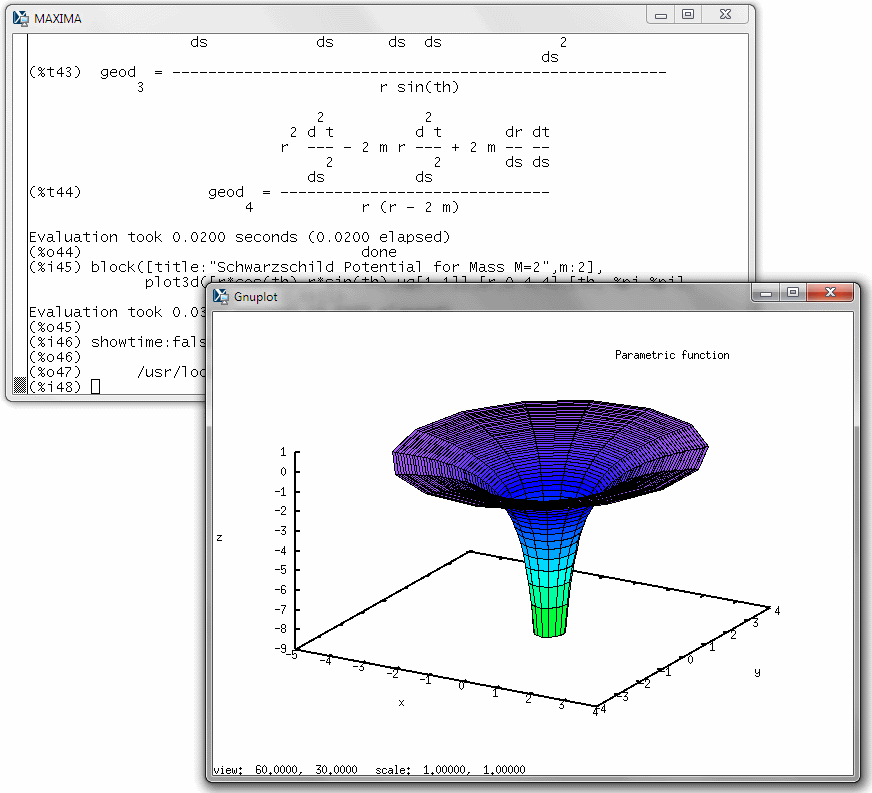
The release turned out to be more of an uphill battle than I anticipated, but in the end, I think everything went glitch-free.
Others have since created installers for different platforms, including Windows.
And I keep promising myself that when I grow up, I will one day understand exactly what git does and how it works, instead of just blindly following arcane scripts…
Years ago, I accepted the role of release manager for the Maxima computer algebra system. It proved to be more laborious than I assumed (mostly for two things: assembling changelogs, and dealing with build glitches) but it still has its upside. Right now, it is my pleasure to announce that Maxima 5.42 has been released on the unsuspecting public. Enjoy!
I have been so busy this week, I forgot to blog about our latest Maxima release, 5.39. Nothing spectacular, just incremental improvements over 5.38; for me, this was a big milestone though as this was the first time that I used a CentOS platform to prepare the release. (Which, incidentally, is why I haven’t done this months ago.)
And SourceForge, kindly enough, once again designated Maxima as one of the site’s Projects of the Week.
Sometime last year, I foolishly volunteered to manage new releases of the Maxima computer algebra system (CAS).
For the past several weeks, I’ve been promising to do my first release, but I kept putting it off as I had other, more pressing work obligations.
Well, not anymore… today, I finally found the time, after brushing up on the Git version management system, and managed to put together a release, 5.38.0.
Maxima is beautiful and incredibly powerful. I have been working on its tensor algebra packages for the past 15 years or so. As far as I know, Maxima is the only general purpose CAS that can derive the field equations of a Lagrangian field theory; for instance, it can derive Einstein’s field equations from the Einstein-Hilbert Lagrangian.
I use Maxima a lot for tensor algebra, though I admit that when it comes to integration, differential equations or plotting, I prefer Maple. Maple’s ODE/PDE solvers are unbeatable. But when it comes to tensor algebra, or just as a generic on-screen symbolic calculator, Maxima wins hands down. I prefer to use its command-line version: Nothing fancy, just ASCII art, but very snappy, very responsive, and does exactly what I want it to do.
So then, Maxima 5.38.0: Say hi to the world. World, this is the latest version of the oldest (nearly half a century old) continuously maintained CAS in existence.
I was having a discussion with a lawyer friend of mine. I was trying to illustrate the difference between the advocating done by lawyers and the scientist’s unbiased (or at least, not intentionally biased) search for the truth. One is about cherry-picking facts and arguments to prove a preconceived notion; the other about trying to understand the world around us.
I told him that anything and the opposite of anything can be proven by cherry-picking facts. Then it occurred to me that it is true even in math. For instance, by cherry-picking facts, I can easily prove that \(2\times 2=5\). Let’s start with three variables, \(a\), \(b\) and \(c\), for which it is true that \(a=b+c\). Then, multiplying by 5 gives
$$5a=5b+5c.$$
Multiplying by 4 and switching the two sides gives
$$4b+4c=4a.$$
Adding these two equations together, we get
$$5a+4b+4c=4a+5b+5c.$$
Subtracting \(9a\) from both sides, we obtain
$$4b+4c-4a=5b+5c-5a,$$
or
$$4(b+c-a)=5(b+c-a).$$
Dividing both sides by \(b+c-a\) gives the final result:
$$4=5.$$
And no, I did not make some simple mistake in my derivation. In fact, I can use computer algebra to obtain the same result, and computers surely don’t lie. Here it is, with Maxima:
(%i1) eq1:5*a=5*b+5*c$ (%i2) eq2:4*b+4*c=4*a$ (%i3) eq3:eq1+eq2$ (%i4) eq4:eq3-9*a$ (%i5) eq5:factor(eq4)$ (%i6) eq6:eq5/(b+c-a); (%o6) 4 = 5
All I had to do to make this happen was to ignore an inconvenient little fact, which is precisely what lawyers (not to mention politicians) do all the time. Surely, if I can prove that \(2\times 2=5\), I can prove anything. So can lawyers and they know it.
Maxima is an open-source computer algebra system (CAS) and a damn good one at that if I may say so myself, being one of Maxima’s developers.
Among other things, Maxima has top-notch tensor algebra capabilities, which can be used, among other things, to work with Lagrangian field theories.
This week, I am pleased to report, SourgeForge chose Maxima as one of the featured open-source projects on their front page. No, it won’t make us rich and famous (not even rich or famous) but it is nice to be recognized.
An interesting anniversary today: 25 years ago, on March 15, 1985, the first ever .com domain name was registered, symbolics.com. The company, in addition to building their own brand of “Lisp Machine” computers, also happened to be selling the commercial version of the MACSYMA computer algebra software. The same software that, in the form of its open-source version, Maxima, continues to evolve thanks to a devoted team of developers… of which I happen to be one.
Alas, Symbolics is no longer, at least not the original company. A privately held company by the same name which obtained much of Symbolics’ assets still sells licenses of the old MACSYMA code.