A beautiful study was published the other day, and it received a lot of press coverage, so I get a lot of questions.
This study shows how, in principle, we could reconstruct the image of an exoplanet using the Solar Gravitational Lens (SGL) using just a single snapshot of the Einstein ring around the Sun.
The problem is, we cannot. As they say, the devil is in the details.
Here is a general statement about any conventional optical system that does not involve more exotic, nonlinear optics: whatever the system does, ultimately it maps light from picture elements, pixels, in the source plane, into pixels in the image plane.
Let me explain what this means in principle, through an extreme example. Suppose someone tells you that there is a distant planet in another galaxy, and you are allowed to ignore any contaminating sources of light. You are allowed to forget about the particle nature of light. You are allowed to forget the physical limitations of your cell phone’s camera, such as its CMOS sensor dynamic range or readout noise. You hold up your cell phone and take a snapshot. It doesn’t even matter if the camera is not well focused or if there is motion blur, so long as you have precise knowledge of how it is focused and how it moves. The map is still a linear map. So if your cellphone camera has 40 megapixels, a simple mathematical operation, inverting the so-called convolution matrix, lets you reconstruct the source in all its exquisite detail. All you need to know is a precise mathematical description, the so-called “point spread function” (PSF) of the camera (including any defocusing and motion blur). Beyond that, it just amounts to inverting a matrix, or equivalently, solving a linear system of equations. In other words, standard fare for anyone studying numerical computational methods, and easily solvable even at extreme high resolutions using appropriate computational resources. (A high-end GPU in your desktop computer is ideal for such calculations.)
Why can’t we do this in practice? Why do we worry about things like the diffraction limit of our camera or telescope?
The answer, ultimately, is noise. The random, unpredictable, or unmodelable element.
Noise comes from many sources. It can include so-called quantization noise because our camera sensor digitizes the light intensity using a finite number of bits. It can include systematic noises due to many reasons, such as differently calibrated sensor pixels or even approximations used in the mathematical description of the PSF. It can include unavoidable, random, “stochastic” noise that arises because light arrives as discrete packets of energy in the form of photons, not as a continuous wave.
When we invert the convolution matrix in the presence of all these noise sources, the noise gets amplified far more than the signal. In the end, the reconstructed, “deconvolved” image becomes useless unless we had an exceptionally high signal-to-noise ratio, or SNR, to begin with.
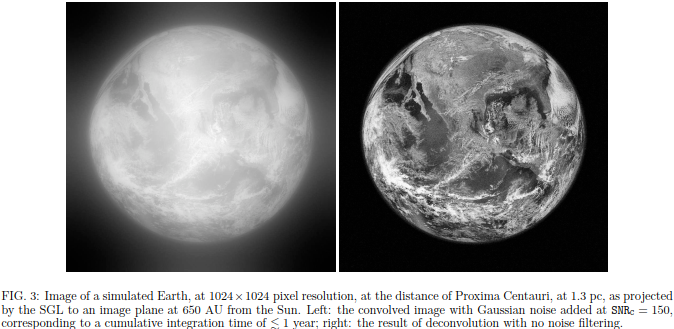
The authors of this beautiful study knew this. They even state it in their paper. They mention values such as 4,000, even 200,000 for the SNR.
And then there is reality. The Einstein ring does not appear in black, empty space. It appears on top of the bright solar corona. And even if we subtract the corona, we cannot eliminate the stochastic shot noise due to photons from the corona by any means other than collecting data for a longer time.
Let me show a plot from a paper that is work-in-progress, with the actual SNR that we can expect on pixels in a cross-sectional view of the Einstein ring that appears around the Sun:
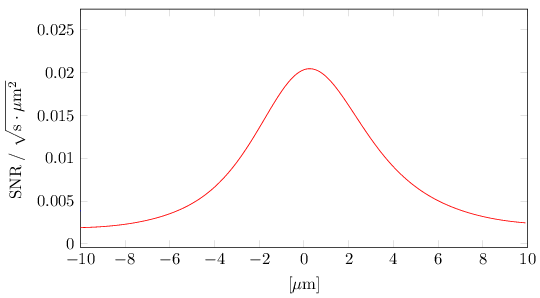
Just look at the vertical axis. See those values there? That’s our realistic SNR, when the Einstein ring is imaged through the solar corona, using a 1-meter telescope with a 10 meter focal distance, using an image sensor pixel size of a square micron. These choices are consistent with just a tad under 5000 pixels falling within the usable area of the Einstein ring, which can be used to reconstruct, in principle, a roughly 64 by 64 pixel image of the source. As this plot shows, a typical value for the SNR would be 0.01 using 1 second of light collecting time (integration time).
What does that mean? Well, for starters it means that to collect enough light to get an SNR of 4,000, assuming everything else is absolutely, flawlessly perfect, there is no motion blur, indeed no motion at all, no sources of contamination other than the solar corona, no quantization noise, no limitations on the sensor, achieving an SNR of 4,000 would require roughly 160 billion seconds of integration time. That is roughly 5,000 years.
And that is why we are not seriously contemplating image reconstruction from a single snapshot of the Einstein ring.