April 2012 – Spinor Info

Commercials on CBC Radio 2

Apr 302012

I am reading about plans to introduce commercials on CBC Radio 2. Looks like a done deal unless the CRTC disagrees, which I think is unlikely.

What has been done to CBC Radio in the past 25 years is just unconscionable. They are turning a once world-class national broadcaster into a run-of-the-mill radio network that is more and more indistinguishable from its commercial counterparts.

Meanwhile, here in Ottawa, the capital of Canada, for much of the day there are no radio stations broadcasting anything that could be described as “high culture”. None. No classical music, no jazz, no arts programs, no literary programs, just commercial music, talk radio and the like.

Oh well. Thanks to the Internet, we can always listen to the BBC. Or ABC from Australia. Or Bartok Radio from Budapest. Or other national broadcasters from countries much smaller and much poorer than Canada who nevertheless believe that investing in high culture is not worthless elitism but an investment in the future.

The day against DRM

Intellectual Property, Internet, Politics 2 Responses »

Apr 292012

I am not the activist type, but I admit I am a little distressed by the fact that no Canadian events appear to be planned on The Day Against DRM.

The reason for my distress? Our federal government is about to enact into law Bill C-11, a bill that will make the simple act of copying a DVD to your computer for convenient viewing, or viewing a DVD purchased abroad using “region free” software, criminally illegal.

2 x 2 = 5

Computer Algebra, Mathematics, Society No Responses »

Apr 242012

I was having a discussion with a lawyer friend of mine. I was trying to illustrate the difference between the advocating done by lawyers and the scientist’s unbiased (or at least, not intentionally biased) search for the truth. One is about cherry-picking facts and arguments to prove a preconceived notion; the other about trying to understand the world around us.

I told him that anything and the opposite of anything can be proven by cherry-picking facts. Then it occurred to me that it is true even in math. For instance, by cherry-picking facts, I can easily prove that $2\times 2=5$. Let’s start with three variables, $a$, $b$ and $c$, for which it is true that $a=b+c$. Then, multiplying by 5 gives

$$5a=5b+5c.$$

Multiplying by 4 and switching the two sides gives

$$4b+4c=4a.$$

Adding these two equations together, we get

$$5a+4b+4c=4a+5b+5c.$$

Subtracting $9a$ from both sides, we obtain

$$4b+4c-4a=5b+5c-5a,$$

$$4(b+c-a)=5(b+c-a).$$

Dividing both sides by $b+c-a$ gives the final result:

$$4=5.$$

And no, I did not make some simple mistake in my derivation. In fact, I can use computer algebra to obtain the same result, and computers surely don’t lie. Here it is, with Maxima:

(%i1) eq1:5*a=5*b+5*c$
(%i2) eq2:4*b+4*c=4*a$
(%i3) eq3:eq1+eq2$
(%i4) eq4:eq3-9*a$
(%i5) eq5:factor(eq4)$
(%i6) eq6:eq5/(b+c-a);
(%o6)                                4 = 5

All I had to do to make this happen was to ignore an inconvenient little fact, which is precisely what lawyers (not to mention politicians) do all the time. Surely, if I can prove that $2\times 2=5$, I can prove anything. So can lawyers and they know it.

Let it snow?

Local Ottawa, Personal, Weather and Climate No Responses »

Apr 232012

April 23, 2012, and this is what I see through my window:

A month ago, I had to run my air conditioner. Grumble.

Happy royal birthday!

Canada, History, Politics 1 Response »

Apr 212012

Her Majesty, Queen Elizabeth II, is 86 years young today, in the 60th year of her reign. She is the last surviving head of state to have served in uniform in the Second World War. May she see many more birthdays in good health and spirit.

Yes, I am a loyalist royalist (or a royalist loyalist?) Canadian. It is one of those very few things on which I see eye-to-eye with conservatives these days.

Princess Elizabeth in the Women’s Auxiliary Territorial Service, 1945.

Last flight of Discovery

Aviation, History, Space No Responses »

Apr 172012

The Space Shuttle Discovery is on its way to its final resting place.

Many lament the end of the Shuttle program. They shouldn’t. Beautiful as these machines were, they really stifled the American space program. For decades, countless billions of dollars were spent… on going around, and around, and around, in low-Earth orbit, ultimately getting nowhere.

When Barack Obama opted for a variant of the Augustine Commission‘s “flexible path” approach, some pundits called it the end of America’s space dominance. I think the contrary is true. Instead of opting for an overly ambitious but ultimately unrealistic space program that would eventually die on the floors of Congress due to lack of funding, Obama chose a space program that places the emphasis on sustainable development: a long term vision of expanding human presence beyond Earth orbit in the solar system, not necessarily with spectacular landings on Mars (however desirable such a landing may be, it’s also insanely risky and expensive) but with building the infrastructure for a permanent human presence beyond the protective shield of the Earth’s radiation belts.

Lies, history and statistics

History, Society, Television No Responses »

Apr 162012

Last night, I was watching a documentary about the 1943 Nazi film Titanic, an attempt by Göbbels to twist the tragic story of the sinking for German propaganda purposes (Briefly: Titanic sank because of the greed and hubris of British capitalists and despite the heroic efforts of a German first officer.)

The story behind the movie is fascinating (director was arrested by the Gestapo and hanged himself, film was banned by Göbbels and only shown in occupied territories, never in Nazi Germany), but then they screw it all up with a complete fabrication. The ship that was used for the filming, the luxury ocean liner SS Cap Arcona, was herself sunk in May 1945 with about 5,000 concentration camp prisoners on board. The sinking happened in part because of a shake-up of responsibilities between Bomber Command and Fighter Command in the RAF, in the wake of the firebombing of Dresden. But according to the film I just saw, the sinking was deliberately planned by the Nazis who filled the ship with flammable fuel and intentionally put it out for the RAF to bomb. This is just a boldfaced lie (it’s not like the Germans had any fuel reserves left in April 1945, and they certainly didn’t need to resort to such an elaborate plot to end the lives of a mere 5,000 people; besides, several ships were hit that day, including an unmarked German hospital ship) and I keep wondering why, nearly 70 years after the end of World War 2, we are still being subjected to wartime propaganda.

Incidentally, the Web page I linked to above states that the sinking of the Cap Arcona was the world’s greatest ship disaster. Not so. That sad distinction belongs to the MV Wilhelm Gustloff, another German ship that was torpedoed by the Soviets in January 1945 while carrying over 10,000 evacuees, mostly civilians. More than 9,000 people died.

And while I was debating with myself whether or not to turn this into a blog post, I was listening to the noon newscast on CTV Ottawa. In the context of a sexual attack this morning on Metcalfe street, the reporter told us that “in a single day, nearly 5,300 cases of sexual assault are reported in Canada”. What? That is a humongous number. It is also wrong. What actually happened in a single day (April 19, 2006) was that nearly 5,300 victims of sexual assault and other violent offences requested assistance from victim service agencies across Canada. The number of “incidents involving sexual offences” was 27,094 in 2002; that translates into about 75 sexual assaults in a single day. Not 5,300.

To paraphrase Mark Twain, there are lies; there is history; and then there are statistics.

But perhaps “damn lies” is just a synonym for history?

Pioneer 10 on The Simpsons

Space, Television No Responses »

Apr 152012

At the very end of tonight’s episode of The Simpsons, just before the end credits, we caught a brief glimpse of Pioneer 10 (or was it 11?), along with an extraterrestrial intently studying Carl Sagan’s famous golden plaque.

But wait a minute… stupid alien is holding the plaque upside-down. No wonder he can’t make sense of it.

And they didn’t get the shape of the RTG fins right. Can’t really blame them; way too many artistic depictions of Pioneer show the generators with the small, rectangular fins that, I believe, were on (non-nuclear) engineering mockups used during testing.

More clever in traffic court than Sheldon Cooper

Physics, Society No Responses »

Apr 152012

Now here is a way to use physics more cleverly than Sheldon Cooper to avoid a costly ticket for a moving violation: http://arxiv.org/abs/1204.0162.

The brief, two-sentence abstract reads: A way to fight your traffic tickets. The paper was awarded a special prize of $400 that the author did not have to pay to the state of California.

Perhaps unsurprisingly, the paper is dated April 1. But the story, it appears, is real nonetheless.

Titanic

History No Responses »

Apr 142012

Exactly 100 years ago these very hours, what was then the most advanced, largest ship in the world hit an iceberg and sank, taking the lives of some 1,500 people.

I first heard about Titanic when I was still a kindergartener. No surprise, perhaps. My father was born in 1906, which means he was almost 6 years of age when Titanic sank. Even in his hometown of Temesvár (present-day Timisoara, Romania) the sinking of the Titanic was big news. Everyone must have been talking about the disaster for days, weeks, months to come, and this must have left quite an impression on my father, who was always interested in things technical. It was from my father that I first heard about things such as an iceberg having 90% of its mass underwater, spark-gap transmitters, Morse code and SOS signals; all in the context of Titanic of course.

I also had a great uncle who was born in 1894. He was the one who taught me how to play chess. He was a young adult already when Titanic sailed… much to his misfortune, it also meant that he was a young adult in 1914, which meant serving in the first World War.

Titanic was a marvelous ship. She was the pinnacle of high-tech engineering. I find it especially haunting that her lights stayed on almost until the very end, thanks to her redundant electrical systems and, just as importantly, her heroic engineers.

Yet she went down, and two years later, the world that created it also went down in flames. I am reminded of a computer game from the 1990s, The Last Express (produced, incidentally, the same year as James Cameron’s Titanic). In this game, the player is tasked with solving a series of murder and conspiracy mysteries… on board the very last Orient Express to travel from Paris to Istambul before the outbreak of the Great War.

I hope we learned more than just the art of building safer ships in the past 100 years.

Physics vs. economics

Economy, Physics 1 Response »

Apr 142012

I just came across this delightful imaginary conversation between a physicist and an economist about the unsustainability of perpetual economic growth.

The physicist uses energy production in his argument: growth at present rates means that in a few hundred years, we’ll produce enough energy to start boiling the oceans. And this is not something that can be addressed easily by the magic of technology. When waste heat is produced, the only way to get rid of it is to radiate it away into space. After about 1400 years of continuous growth, the Earth will be radiating more energy (all man-made) than the Sun, which means it would have to be a lot hotter than the Sun, on account of its smaller size. And in about 2500 years, we would exceed the thermal output of the whole Milky Way.

This, of course, is nonsense, which means terrestrial energy production will be capped eventually by basic physics. If GDP would continue to grow nonetheless, it would mean that the price of energy relative to other stuff would decrease to zero. This is also nonsense, since a limited resource cannot become arbitrarily cheap. But that means GDP growth must also be capped.

What I liked about this argument is that it is not emotional or ideological; it’s not about hugging trees or hating capitalism. It is about basic physics and elementary logic that is difficult to escape. In fact, it can be put in the form of equations. Our present energy production $P_0$ is approximately 15 TW, which is about 0.002% of the Sun’s output that reaches the Earth:

\begin{align}
P_0&\simeq 1.5 \times 10^{13}~\rm{W},\\
P_\odot&\simeq 7 \times 10^{17}~\rm{W},\\
\eta_0&=P_0/P_\odot \sim 0.002\%.
\end{align}

For any other value of $\eta$, there is a corresponding value of $P$:

\begin{align}
P=\eta P_\odot.
\end{align}

Now all we need is to establish a maximum value of $\eta$ that we can live with; say, $\eta_{\rm max}=1\%$. This tells us the maximum amount of energy that we can produce here in the Earth without cooking ourselves:

\begin{align}
P_{\rm max}=\eta_{\rm max}P_\odot.
\end{align}

On the economic side of this argument, there is the percentage of GDP that is spent on energy. In the US, this is about 8%. For lack of a better value, let me stick to this one:

\begin{align}
\kappa_0\sim 8\%.
\end{align}

How low can $\kappa$ get? That may be debatable, but it cannot become arbitrarily low. So there is a value $\kappa_{\rm min}$.

The rest is just basic arithmetic. GDP is proportional to the total energy produced, divided by $\kappa$:

\begin{align}
{\rm GDP}&\propto \frac{\eta}{\kappa}P_\odot,\\
{\rm GDP}_{\rm max}&\propto \frac{\eta_{\rm \max}}{\kappa_{\rm min}}P_\odot,
\end{align}

And in particular:

\begin{align}
{\rm GDP}_{\rm max}&=\frac{\eta_{\rm max}\kappa_0}{\eta_0\kappa_{\rm min}}{\rm GDP}_0,
\end{align}

where ${\rm GDP}_0$ is the present GDP.

We know $\eta_0\sim 0.002\%$. We know $\kappa_0=8\%$. We can guess that $\eta_{\rm max}\lesssim 1\%$ and $\kappa_{\rm min}\gtrsim 1\%$. This means that

\begin{align}
{\rm GDP}_{\rm max}\lesssim 4,000\times {\rm GDP}_0.
\end{align}

This is it. A hard limit imposed by thermodynamics. But hey… four thousand is a big number, isn’t it? Well… sort of. At a constant 3% rate of annual growth, the economy will increase to four thousand times its present size in a mere 280 years or so. One may tweak the numbers a little here and there, but the fact that physics imposes such a hard limit remains. The logic is inescapable.

Or is it? The word “escape” may be appropriate here for more than one reason, as there is one obvious way to evade this argument: escape into space. In a few hundred years, humanity may have spread throughout the solar system, and energy amounts enough to boil the Earth’s oceans may be powering human colonies in the hostile (and cold!) environments near the outer planets.

That is, if humans are still around a few hundred years from now. One can only hope.

A day black cats like

Pop culture No Responses »

Apr 132012

Almost forgot: it’s Friday the 13th again!

The thermal origin of the Pioneer anomaly

Personal, Physics, Space 1 Response »

Apr 122012

Our second short paper has been accepted for publication in Physical Review Letters.

I have been involved with Pioneer 10 and 11 in some fashion since about 2002, when I first began corresponding with Larry Kellogg about the possibility of resurrecting the telemetry data set. It is thanks the Larry’s stamina and conscientiousness that the data set survived.

I have been involved actively in the research of the Pioneer anomaly since 2005. Seven years! Hard to believe.

This widely reported anomaly concerns the fact that when the orbits of Pioneer 10 and 11 are accurately modeled, a discrepancy exists between the modeled and measured frequency of the radio signal. This discrepancy can be resolved by assuming an unknown force that pushes Pioneer 10 an 11 towards the Earth or the Sun (from that far away, these two directions nearly coincide and cannot really be told apart.)

One purpose of our investigation was to find out the magnitude of the force that arises as the spacecraft radiates different amounts of heat in different directions. This is the concept of a photon rocket. A ray of light carries momentum. Hard as it may appear to believe at first, when you hold a flashlight in your hands and turn it on, the flashlight will push your hand backwards by a tiny force. (How tiny? If it is a 1 W bulb that is perfectly efficient and perfectly focused, the force will be equivalent to about one third of one millionth of a gram of weight.)

On Pioneer 10 and 11, we have two main heat sources. First, there is electrical heat: all the instruments on board use about 100 W of electricity, most of which is converted into heat. Second, electricity is produced, very inefficiently, by a set of four radioisotope thermoelectric generators (RTGs); these produce more than 2 kW of waste heat. All this heat has to go somewhere, and most of this heat will be dissipated preferably in one direction, behind the spacecraft’s large dish antenna, which is always pointed towards the Earth.

The controversial question was, how much? How efficiently is this heat converted into force?

I first constructed a viable thermal model for Pioneer 10 back in 2006. I presented results from custom ray-tracing code at the Pioneer Explorer Collaboration meeting at the International Space Science Institute in Bern, Switzerland in February 2007:

With this, I confirmed what has already been suspected by others—notably, Katz (Phys. Rev. Letters 83:9, 1892, 1999); Murphy (Phys. Rev. Letters 83:9, 1890, 1999); and Scheffer (Phys. Rev. D, 67:8, 084021, 2003)—that the magnitude of the thermal recoil force is indeed comparable to the anomalous acceleration. Moreover, I established that the thermal recoil force is very accurately described as a simple linear combination of heat from two heat sources: electrical heat and heat from the RTGs. The thermal acceleration $a$ is, in fact

$$a=\frac{1}{mc}(\eta_{\rm rtg}P_{\rm rtg} + \eta_{\rm elec}P_{\rm elec}),$$

where $c\simeq 300,000~{\rm km/s}$ is the speed of light, $m\simeq 250~{\rm kg}$ is the mass of the spacecraft, $P_{\rm rtg}\sim 2~{\rm kW}$ and $P_{\rm elec}\sim 100~\rm {W}$ are the RTG heat and electrical heat, respectively, and $\eta_{\rm rtg}$ and $\eta_{\rm elec}$ are “efficiency factors”.

This simple force model is very useful because it can be incorporated directly into the orbital model of the spacecraft.

In the years since, the group led by Gary Kinsella constructed a very thorough and comprehensive model of the Pioneer spacecraft, using the same software tools (not to mention considerable expertise) that they use for “live” spacecraft. With this model, they were able to predict the thermal recoil force with the greatest accuracy possible, at different points along the trajectory of the spacecraft. The result can be compared directly to the acceleration that is “measured”; i.e., the acceleration that is needed to model the radio signal accurately:

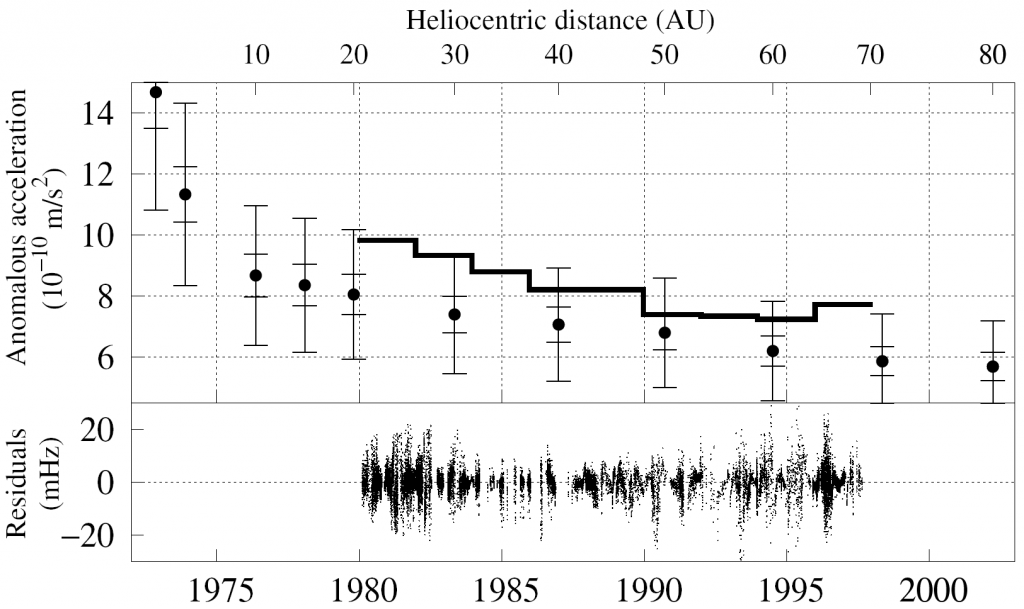
In this plot, the step-function like curve (thick line) is the acceleration deduced from the radio signal frequency. The data points with vertical error bars represent the recoil force calculated from the thermal model. They are rather close. The relatively large error bars are due primarily to the fact that we simply don’t know what happened to the white paint that coated the RTGs. These were hot (the RTGs were sizzling hot even in deep space) and subjected to solar radiation (ultraviolet light and charged particles) so the properties of the paint may have changed significantly over time… we just don’t know how. The lower part of the plot shows just how well the radio signal is modeled; the average residual is less than 5 mHz. The actual frequency of the radio signal is 2 GHz, so this represents a modeling accuracy of less than one part in 100 billion, over the course of nearly 20 years.

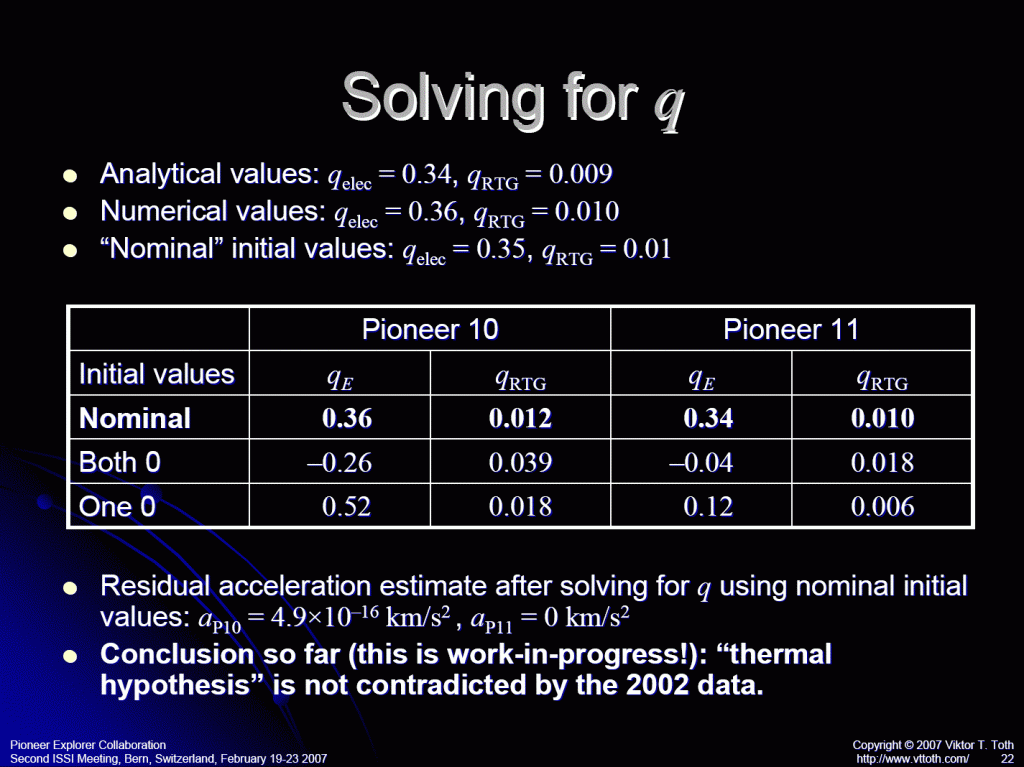
In terms of the above-mentioned efficiency factors, the model of Gary’s group yielded $\eta_{\rm rtg}=0.0104$ and $\eta_{\rm elec}=0.406$.

But then, as I said, we also incorporated the thermal recoil force directly into the Doppler analysis that was carried out by Jordan Ellis. Jordan found best-fit residuals at $\eta_{\rm rtg}=0.0144$ and $\eta_{\rm elec}=0.480$. These are somewhat larger than the values from the thermal model. But how much larger?

We found that the best way to answer this question was to plot the two results in the parameter space defined by these two efficiency factors:

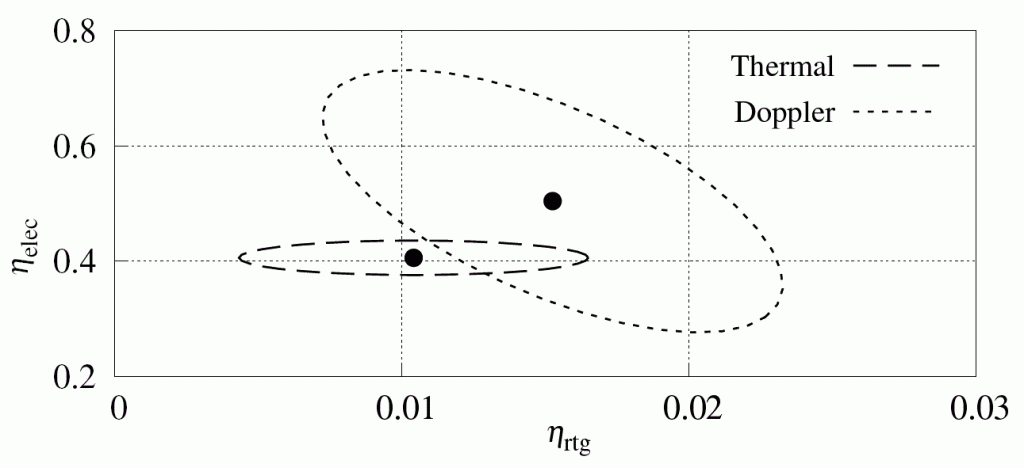
The dashed ellipse here represents the estimates from the thermal model and their associated uncertainty. The ellipse is elongated horizontally, because the largest source of uncertainty, the degradation of RTG paint, affects only the $\eta_{\rm rtg}$ factor.

The dotted ellipse represents the estimates from radio signal measurements. The formal error of these estimates is very small (the error ellipse would be invisibly tiny). These formal errors, however, are calculated by assuming that the error in every one of the tens of thousands of Doppler measurements arises independently. In reality, this is not the case: the Doppler measurements are insanely accurate, any errors that occur are a result of systematic mismodeling, e.g., caused by our inadequate knowledge of the solar system. This inflates the error ellipse and that is what was shown in this plot.

Looking at this plot was what allowed us to close our analysis with the words, “We therefore conclude that at the present level of our knowledge of the Pioneer 10 spacecraft and its trajectory, no statistically significant acceleration anomaly exists.”

Are there any caveats? Not really, I don’t think, but there are still some unexplored questions. Applying this research to Pioneer 11 (I expect no surprises there, but we have not done this in a systematic fashion). Modeling the spin rate change of the two spacecraft. Making use of radio signal strength measurements, which can give us clues about the precise orientation of the spacecraft. Testing the paint that was used on the RTGs in a thermal vacuum chamber. Accounting for outgassing. These are all interesting issues but it is quite unlikely that they will alter our main conclusion.

On several occasions when I gave talks about Pioneer, I used a slide that said, in big friendly letters,

PIONEER 10/11 ARE THE MOST PRECISELY NAVIGATED DEEP SPACE CRAFT TO DATE.

And they confirmed the predictions of Newton and Einstein, with spectacular accuracy, by measuring the gravitational field of the Sun in situ, all the way up to about about 70 astronomical units (the distance of the Earth from the Sun).

Göbekli Tepe

Culture, History, Religion No Responses »

Apr 102012

I was reading about a place called Göbekli Tepe today.

This is a place in southeastern Turkey. It is the site of an archeological excavation; they are exploring the ruins of an old temple.

The ruins of a really old temple. Really, really, really old.

How old? Well… when the first Egyptian pyramid was still on the drawing board, Göbekli Tepe was already some 6,000 years of age. Indeed, when Göbekli Tepe was built, the place where I now live, Ottawa, was still covered by the Champlain Sea. The oldest ruins at Göbekli Tepe are 11,500 years old, take or leave a few centuries.

That is an astonishing age for a major stone structure like this. Wikipedia tells me that it was built by hunter-gatherers, but I have a hard time accepting that hypothesis: Stone construction on this scale requires highly specialized skills not to mention the organization of the necessary labor force. Maybe I lack imagination but I just can’t see how hunter-gatherer tribes, even if they have permanent village settlements, would be able to accomplish something on this scale.

But if it wasn’t hunter-gatherers, who were they? What kind of civilization existed in that part of the world 11,500 years ago that we know nothing about?

Happy Easter!

Culture, History, Personal No Responses »

Apr 082012

I have no delusions about my abilities as a graphic artist, but hey, it’s from the heart. Happy Easter, everyone!

As to why we choose to celebrate the gruesome death on the cross and subsequent resurrection of a young man some 2,000 years ago, one whose sole crime was that he was preaching love and understanding among neighbors, with bunny rabbits laying gaudy-colored eggs and such nonsense, I have no idea. But then, I am just the clueless atheist here, so what do I know?

I only wish more people actually listened to that young man’s message, instead of choosing hatred and violence. The world would indeed be a better place.