Solar Gravitational Lens
In the past year (2017), I began collaborating with Slava Turyshev on the topic of the Solar Gravitational Lens, or SGL. Slava has done a tremendous amount of work on the subject already, so I feel privileged to be able to add my contribution.
The concept is simple. The Sun bends rays of light. Rays passing on both sides of the Sun eventually meet. At this location, with suitable instrumentation, it is possible to form an image. And this “telescope” has astonishing powers of resolution and light amplification, which makes it possible, in principle, to use it to obtain a detailed image of a distant Earth-like planet in a faraway solar system.
The challenges, on the other hand…
For starters, the focal region of the Sun begins at around 550 astronomical units (AU). One AU is the distance between the Earth and the Sun. Our most distant spacecraft to date, Voyager 1, is about 140 AU from the Sun, and it took the spacecraft forty years to get there. Nonetheless, it is possible to build a vehicle that can travel to 550 AU in 20-30 years, so the basic concept is technologically feasible.
Next, the spacecraft would need to be positioned exactly on the opposite side of the Sun relative to the object being imaged. This is harder than it appears. The remote planet is not a stationary target: It is orbiting its own sun, its orbit may be perturbed by the gravity of its satellite(s) and other planets, and its sun, too, is moving across the sky. Moreover, our own Sun is not staying in place either, as it is being yanked about by the gravity of its planets, notably Jupiter.
Third, the SGL suffers from spherical aberration. It does not have a focal point; rather, light is focused along a focal line. On the one hand, this is good news, because a spacecraft does not have to stop once it reaches the beginning of the focal line; it can continue receding from the Sun as it completes its imaging campaign. On the other hand, it means that any image is necessarily blurry, and requires serious post-processing, deconvolution, for it to be useful.
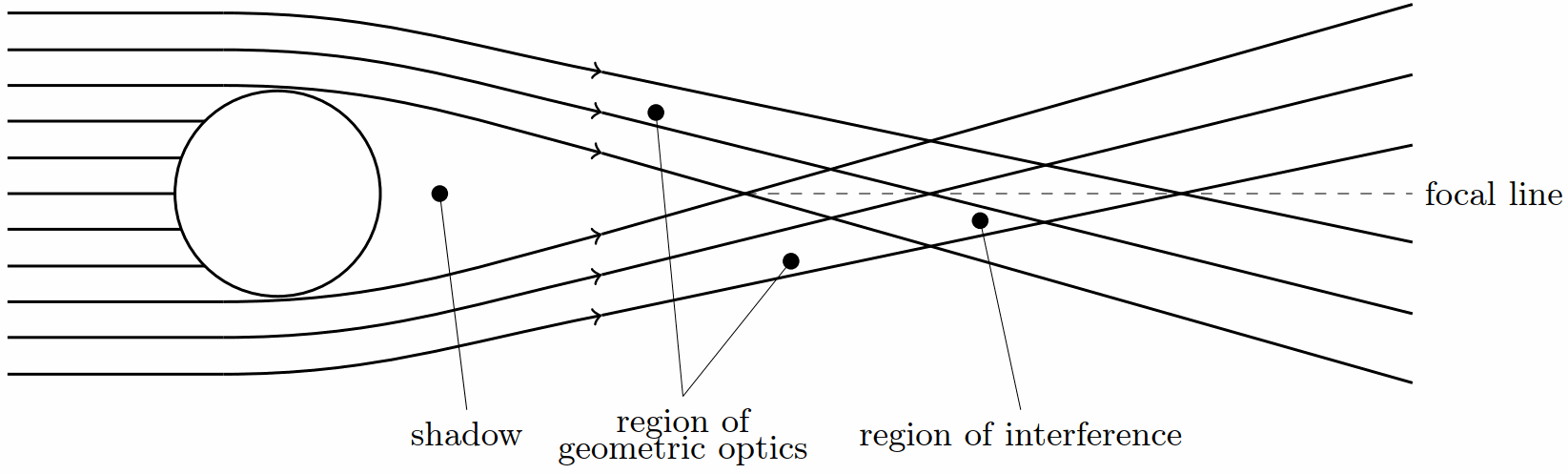
In fact, let me pause here for a moment and elaborate a little bit on how this image is formed. The SGL itself is not really a telescope. Rather, the light that it amplifies appears, as seen from the focal line, as a ring around the Sun.This would be a famous Einstein ring, as demonstrated in this NASA video:
Light in the Einstein ring comes predominantly from the region of the distant object that is exactly on the opposite side of the Sun relative to you, but there is plenty of contamination from neighboring regions as well. As you move laterally (perpendicular to the focal line), the Einstein ring changes, its light now being dominated by a different region of the distant object.
So there you have it: a spacecraft can “scan” the image plane, one “pixel” at a time, while collecting light from the totality of the Einstein ring. It is easy to calculate that each square meter pixel in the image plane corresponds, approximately, to a 100 square kilometer region on the surface of the distant object being imaged. By moving around a roughly one square kilometer region in the image plane, a probe can scan the roughly 100 million square kilometer cross-section of an Earth-like exoplanet at megapixel resolution.
Why one square meter “pixels”? The actual angular resolution of the SGL at optical wavelengths is better, actually. Here is the light amplification gain of the SGL at the near infrared wavelength of 1 micron, at a distance of 600 AU (solid line) vs. 1000 AU (dashed line):
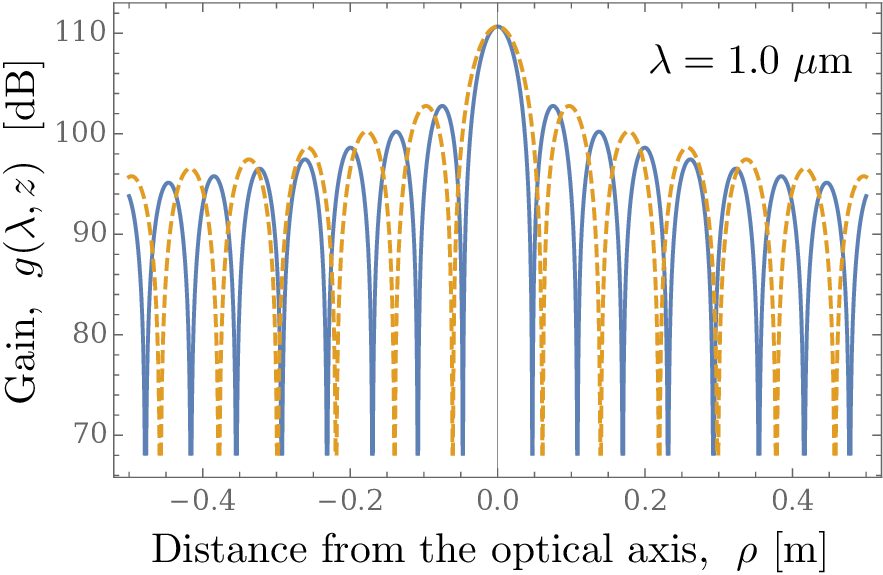
However, we must not forget what we are looking at: a thin ring around the very bright Sun. Light from the Sun itself must be blocked out somehow if we wish to be able to measure the brightness of the ring. This can be done using a coronagraph, but in order for the coronagraph to work, we first must be able to resolve the solar disk. For this, a telescope of sufficient aperture (at least a 1-meter telescope) will be needed.
In addition to spherical aberration, the SGL also suffers from astigmatism. This is due to two factors. First, the Sun is slightly oblate, as a result of its rotation. Second, the rotation itself also contributes a small general relativistic correction; this value is tiny but nonetheless, it is noticeable. It must be accounted for when the SGL’s so-called point-spread function (PSF) is calculated in three dimensions, as this will form the basis of accurate deconvolution.
Next comes another factor of considerable difficulty: if we try to capture an image of a distant planet, we are not looking at a static target. Imagine trying to image the Earth one pixel at a time, slowly (over the course of days, weeks, months, maybe even years) building a full image. Meanwhile, the Earth changes. It is illuminated from varying directions as it travels around the Sun. It may occasionally be obscured by the Moon. It rotates around its own axis. Its cloud cover changes. Even the surface changes, as vegetation comes and goes, as ice caps grow and shrink.
Some of these changes (e.g., illumination, rotation) can be modeled, and that is a good thing: they can in fact help with the deconvolution process. But other changes (such as weather patterns) are more or less random, unpredictable. In some cases, it might be possible to filter out such contributions as noise, but nonetheless, what we are really trying to reconstruct is a dynamic view of the distant planet, evolving over time.
Lastly, although the Einstein-ring forms around the Sun, it is still well within the solar corona. As it turns out, this is less of a problem than one might think. First, the Einstein ring is thin but bright; compared to its brightness, contribution from the solar corona can be neglected as noise. Second, the diffractive effects of the solar corona (which is really just the glowing, but otherwise transparent, upper atmosphere of the Sun) are negligible at optical frequencies.
So there you have it. The challenges that are needed to be overcome include:
- Getting there (travel time of several decades);
- Operating there (reliable operation for several years while data are collected);
- Communication (four times as distant as our farthest spacecraft to date);
- Precise dynamic positioning (moving target, moving Sun);
- Blocking out light from the Sun;
- Accurate modeling of image formation;
- Time-varying target (illumination, rotation, clouds, surface changes, etc.);
- Deconvolution (data collected one pixel at a time).
One possible way to overcome the technical challenges is to use not a single spacecraft but a swarm, perhaps even several swarms, working in tandem, offering redundancy and speeding up image collection.
We have already written a number of papers and articles about this topic. Some of these are listed below. So far, our main focus has been a wave-theoretical treatment of the spherical Sun. Simple geometric optics will not do, despite the fact that we are talking about “rays” of light. What we need to know is how the light spreads out near the focal line, and for this, it is necessary to describe how the wavefront of a plane electromagnetic wave is distorted by the Sun.
As it turns out, much of the mathematical machinery is readily available, used in nuclear physics to describe scattering in a Coulomb field. In the simplest case, the solution is given in the form of hypergeometric functions, which yield a neat pattern characterizing the waveform, shown here in a visually exaggerated case:

If you just look at this image for a few seconds, an ever so faint concentric pattern should become apparent. This is indeed how the waveform can be characterized: it is the combination of a deflected plane wave and a perturbed spherical wave. It is this waveform that yields the gain pattern that was shown in the preceding figure.
The math becomes more complicated as we add contributions from deviations of spherical symmetry by the Sun, the solar atmosphere, and solar rotation, but the basic principles remain the same.
The end result of this effort is an accurate, well-tested PSF, which forms the basis of the deconvolution process. This is illustrated by the following simulated example, starting with a monochromatic image of the Earth:

This image is badly mangled by the SGL, which deposits the following on an imaginary projection screen in the image plane:

Knowledge of the PSF allows us to deconvolve the image with a moderate loss of information:

Key to deconvolution is a theorem that reduces the task to a Fourier transform of the convolved image, to be divided by the Fourier transform of the PSF; the original image can then be obtained by performing an inverse Fourier transform.
Each of the pixels before deconvolution are obtained by physically positioning a spacecraft that looks at the Sun and measures light coming from the Einstein ring that appears around the Sun, made up from light coming from the distant planet on the other side of the Sun.
Ignoring light from the Sun and the solar corona, a spacecraft that moves perpendicular to the optical axis (the imaginary line connecting the distant target with the center of the Sun and extended further on the opposite side of the Sun, where the spacecraft is located) would see the Einstein ring much like in this brief animation:
The somewhat thick appearance of the Einstein ring is due to the limited resolution of the 1-meter telescope. A larger telescope would use a correspondingly thinner ring, but no telescope of practical size would be capable of resolving the ring. That’s okay; the information that is needed to reconstruct the image of the exoplanet is the total amount of light collected from the ring.
- Slava G. Turyshev, “Wave-theoretical description of the solar gravitational lens,” Phys. Rev. D 95, 084041 (2017), arXiv:1703.05783 [gr-qc]
- Slava G. Turyshev and Viktor T. Toth, “Diffraction of light by the solar gravitational lens: a wave-theoretical treatment,” Phys. Rev. D 96, 024008 (2017), arXiv:1704.06824 [gr-qc]
- Slava G. Turyshev and Viktor T. Toth, “Wave-optical treatment of the shadow cast by a large sphere,” Phys. Rev. A 97, 033810 (2018), arXiv:1801.06253 [gr-qc]
- Slava G. Turyshev and Viktor T. Toth, “Diffraction of light by plasma in the solar system”, Journal of Optics 21(4):045601 (2019), arXiv:1805.00398 [physics.optics]
- Slava G. Turyshev and Viktor T. Toth, “Diffraction of light by the gravitational field of the Sun and the solar corona”, Phys. Rev. D 99, 024044, arXiv:1810.06627 [gr-qc]
- Slava G. Turyshev and Viktor T. Toth, “Optical properties of the solar gravitational lens in the presence of the solar corona”, European Physical Journal Plus (2019) 134(2):63, arXiv:1811.06515 [gr-qc]
- Slava G. Turyshev, Michael Shao, Leon Alkalai, Nitin Aurora, Darren Garber, Henry Helvajian, Tom Heinsheimer, Siegfried Janson, Jared R. Males, Dmitri Mawet, Roy Nakagawa, Seth Redfield, Janice Shen, Nathan Strange, Mark R. Swain, Viktor T. Toth, Phil A. Willems, John L. West, Stacy Weinstein-Weiss, Hanying Zhou, “Direct Multipixel Imaging and Spectroscopy of an Exoplanet with a Solar Gravity Lens Mission,” Final Report for the NASA’s Innovative Advanced Concepts (NIAC) Phase I proposal, arXiv:1802.08421 [astro-ph.IM]
- Slava G. Turyshev, Michael Shao, Janice Shen, Hanying Zhou, Viktor T. Toth, Louis Friedman, Leon Alkalai, Nitin Arora, Darren D. Garber, Henry Helvajian, Thomas Heinsheimer, Siegfried W. Janson, Les Johnson, Jared R. Males, Roy Nakagawa, Seth Redfield, Nathan Strange, Mark R. Swain, David Van Buren, John L. West, Stacy Weinstein-Weiss, “Recognizing the Value of the Solar Gravitational Lens for Direct Multipixel Imaging and Spectroscopy of an Exoplanet”, A White Paper to the National Academy of Sciences Committee on an Exoplanet Science Strategy Call for Papers, arXiv:1803.04319 [astro-ph.IM]
- Slava G. Turyshev, Michael Shao and Viktor T. Toth, “Putting gravity to work: Imaging of exoplanets with the solar gravitational lens”, Int. J. Mod. Phys. D28 (2019)
- Slava G. Turyshev and Viktor T. Toth, “Imaging extended sources with the solar gravitational lens”, Phys. Rev. D 100, 084018 (2019), arXiv:1908.01948 [gr-qc]
- Slava G. Turyshev and Viktor T. Toth, “Photometric imaging with the solar gravitational lens”, arXiv:1909.03116 [astro-ph.IM]
- Slava G. Turyshev and Viktor T. Toth, “Image formation process with the solar gravitational lens”, arXiv:1911.03260 [gr-qc]