Just a maintenance release but still: I completed the process to release Maxima 5.48.1.
Hope it will serve the community well. I know I’ll be using it a lot.
Just a maintenance release but still: I completed the process to release Maxima 5.48.1.

Hope it will serve the community well. I know I’ll be using it a lot.
I just completed the process to release Maxima 5.48.
The new version introduces several noteworthy enhancements for symbolic computation, with improvements in performance, functionality, and user experience.
Highlights:
– Unicode-enabled output (when supported by the Lisp compiler)
– Numerous performance improvements across core routines
– New package for symbolic radical denesting
– New package for inferring closed-form expressions from sequences
– New package for simplification of gamma functions
– Resolution of more than 150 tickets, spanning both long-standing and recent bugs
Developed in Common Lisp, Maxima remains a reliable and customizable tool for research, education, science, and engineering.
To install, explore, or contribute: https://maxima.sourceforge.io
I briefly revived a piece of software I wrote last year, modeling the effect of multiple gravitational lenses. I long wanted to do this, it’s just a tad time consuming: to use my software for animations, I need to generate images one frame at a time.
What I wanted to do is an animation that shows what an actual galaxy (as opposed to a point source of light) would look like when lensed. The galaxy in question is NGC-4414:

Nice spiral, isn’t it. Well, here’s what we’d see if we viewed it through an imperfect alignment of four gravitational lenses:
I could watch this animation for hours.
Recently, I published a paper on arXiv about a very serious subject concerning a certain animal species and gravitation. The fact that the paper appeared on arXiv on a particular, notable date is, of course, pure coincidence. This is also evidenced by the fact that the paper received serious attention, in particular by the podcaster physicist Dr. Blitz, on YouTube.
I am very grateful that Dr. Blitz found my paper worthy of an “A+”. I wish I could have him as the referee of some of my other papers!
Today, I am proud to announce what I consider my most important paper yet.
I consider it especially fortunate that it managed to appear at the very top of the listing of new papers in the subject group general relativity and quantum cosmology, on this important date.
Needless to say, I am very proud of my work.
So I am a friend of arXiv. It’s true. I may have been critical of some of their processes from time to time, but I appreciate the absolutely invaluable service that they provide.
So yes, I am a friend of theirs. And now it’s official! They sent me this nice certificate, recognizing my contribution, responding to their request to help test a new upload page.

I was, by my count, one of 79 folks who did so. I am surprised; I expected more. I also feel a bit guilty that I only tested their new submission system once. (It was glitch-free, apart from some issue with HTML generation that, as far as I know, was not even part of the actual test.) Still, it is nice that they sent us these little certificates. It may not pay the bills or buy groceries, but I am proud to be their friend.
Considering our age and our lives, we are probably less exposed than most to the likely consequences of the dramatic changes in geopolitics that are about to unfold, threatening, never mind threatening, much more likely irreversibly damaging, destroying the rules-based world order that characterized the past 80 years. Nonetheless, I feel depressed, frustrated, anxious to the point that I no longer even enjoy some of my favorite television shows. Something as mild as a mistaken identity or a shared secret is enough to trigger a sense of anxiety, which I do not welcome.
Instead, I need distractions. Seriously, all I want to do is to play with our cats or dig into physics. Preferably both. Yes, I often consult with our cats when I think about physics.
Earlier tonight, I was thinking about the Einstein stress-energy-momentum pseudotensor and its possible uses, despite its shortcomings. The nonlocality of the energy of the gravitational field is a fascinating topic, and I keep wondering if it is directly connected somehow to the quantum nature of the universe in which we live.
So we studied high school chemistry. Covalent bonds. We learned about nice, well-behaved molecules. Carbon, for instance, with a valence of 4. Hydrogen, 1.
Next, shalt thou combine the two. For each carbon, shalt thou count four hydrogen atoms, no more, no less. Four shall be the number thou shalt count, and the number of the counting shall be four. Five shalt thou not count, neither count thou three, excepting that thou then proceed to four. Six is right out. Once the number four, being the fourth number, be reached, then regardest thou the newly made Methane Atom.
After these magic incantations, you turn around, smugly satisfied with your knowledge of chemistry, content that all is well in the world, and then someone shoves this under your nose:
It’s called methanium. It’s really just an ion, an extra proton stuck to that methane atom. It really does not want to exist, so much so, it’s a superacid, which is to say its acidity is greater than that of sulfuric acid.
Okay, so maybe methanium is not quite as evil as dimethylmercury, which really should have no right to exist in a sensible universe, but I daresay, the very existence of methanium already should inform us that we do not live in a sensible universe.

I was reading about Borwein integrals.
Here’s a nice result:
$$\int_0^\infty dx\,\frac{\sin x}{x}=\frac{\pi}{2}.$$
Neat, is it not. Here’s another:
$$\int_0^\infty dx\,\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}=\frac{\pi}{2}.$$
Jumping a bit ahead, how about
$$\int_0^\infty dx\,\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}…\frac{\sin (x/13)}{x/13}=\frac{\pi}{2}.$$
Shall we conclude, based on these examples, that
$$\int_0^\infty dx\,\prod\limits_{k=0}^\infty\frac{\sin (x/[2k+1])}{x/[2k+1]}=\frac{\pi}{2}?$$
Not so fast. First, consider that
$$\int_0^\infty dx\,\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}…\frac{\sin (x/15)}{x/15}=\frac{935615849426881477393075728938}{935615849440640907310521750000}\frac{\pi}{2}\approx\frac{\pi}{2}-2.31\times 10^{-11}.$$
Or how about
\begin{align}
\int_0^\infty&dx\,\cos x\,\frac{\sin x}{x}=\frac{\pi}{4},\\
\int_0^\infty&dx\,\cos x\,\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}=\frac{\pi}{4},\\
…\\
\int_0^\infty&dx\,\cos x\,\frac{\sin x}{x}…\frac{\sin (x/111)}{x/111}=\frac{\pi}{4},
\end{align}
but then,
$$\int_0^\infty dx\,\cos x\,\frac{\sin x}{x}…\frac{\sin (x/113)}{x/113}\approx\frac{\pi}{4}-1.1162\times 10^{-138}.$$
There is a lot more about Borwein integrals on Wikipedia, but I think even these few examples are sufficient to convince us that, never mind the actual, physical universe, even the Platonic universe of mathematical truths is fundamentally evil and unreasonable.

Here is one of my cherished possessions. A book, with an inscription:

The inscription, written just over 50 years ago, explains that I received this book from my grade school, in recognition for my exceptional results in mathematics as a sixth grade student. (If memory serves me right, this was the year when I unofficially won the Pest county math championship… for eighth graders.)
The book is a Hungarian-language translation of a British volume from the series Mathematics: A New Approach, by D. E. Mansfield and others, published originally in the early 1960s. I passionately loved this book. It was from this book that I first became familiar with many concepts in trigonometry, matrix algebra, and other topics.
Why am I mentioning this volume? Because the other day, the mailman arrived with an Amazon box containing a set of books. A brand new set of books, published in 2024. A series of mathematics textbooks for middle school and high school students, starting with this volume for 6th and 7th graders:
My instant impression: As a young math geek 50 years ago, I would have fallen in love with these books.
The author, André Cabannes, is known, among other things, as Leonard Susskind’s co-author of General Relativity, the latest book in Susskind’s celebrated Theoretical Minimum series. Cabannes also published several books in his native French, along with numerous translations.
His Middle School Mathematics and High School Mathematics books are clearly the works of passion by a talented, knowledgeable, dedicated author. The moment I opened the first volume, I felt a sense of familiarity. I sensed the same clarity, same organization, and the same quality of writing that characterized those Mansfield books all those years ago.
Make no mistake about it, just like the Mansfield books, these books by Cabannes are ambitious. The subjects covered in these volumes go well beyond, I suspect, the mathematics curricula of most middle schools or high schools around the world. So what’s wrong with that, I ask? A talented young student would be delighted, not intimidated, by the wealth of subjects that are covered in the books. The style is sufficiently light-hearted, with relevant illustrations on nearly every page, with the occasional historical tidbit or anecdote, making it easier to absorb the material. And throughout, there is an understanding of the practical nature, utility of mathematics, that is best summarized by the words on the books’ back cover: “Mathematics is not a collection of puzzles or riddles designed to test your intelligence; it is a language for describing and interacting with the world.”
Indeed it is. And these books are true to the author’s words. The subjects may range from the volume of milk cartons through the ratio of ingredients in a cake recipe all the way to the share of the popular vote in the 2024 US presidential election. In each of these examples, the practical utility of numbers and mathematical methods is emphasized. At the same time, the books feel decidedly “old school” but in a good sense: there is no sign of any of the recent fads in mathematics education. The books are “hard core”: ideas and methods are presented in a straightforward way, fulfilling the purpose of passing on the accumulated knowledge of generations to the young reader even as motivations and practical utility are often emphasized.
This is how my love affair with math began when I was a young student, all those years ago. The books that came into my possession, courtesy of both my parents and my teachers, were of a similar nature: they offered robust knowledge, practical utility, clear motivation. Had it existed already, this wonderful series by Cabannes would have made a perfect addition to my little library 50 years ago.
I keep being asked: When will you write a book already? And true, I have several half-baked book ideas that I am contemplating. One of them was going to be a book discussing some key concepts in physics by offering both an accessible narrative and a technical background.
Well, it appears I have been scooped, if that’s the right word! I first heart of Brent Lewis’s project when he contacted me last year, sending me a prerelease copy of Theoretical Physics for the Masses. Oh my, I thought, this is the book I wanted to write!
Or, well, as close as possible to the book I wanted to write, considering that it is not my brainchild and as such, Lewis’s selection of topics differed slightly from mine. Anyhow, long story short, the book is now published by World Scientific, a reputable publisher of books and numerous journals. I hope that it will mean a decent effort at marketing and Lewis will be able to collect royalties on many copies.
Considering the breadth of subjects, the book is surprisingly thin: Just over 180 pages, with appendices included. The main body part is less than 60 pages, however; the remainder are the technical appendices. Depending on how you look at it, this could be considered a bug or a feature.
Who is this book for? Let’s face it, the technical appendices are not for the faint-hearted. Lagrangian field theory, the equations of general relativity, Fourier-decomposition of a scalar field and derivation of the corresponding quantum field theory propagator, even a brief overview of the key features of bosonic string theory: this is not high school mathematics. Nor can we possible expect a thorough treatment of these subjects in such a thin volume.
Yet this book reminds me of a much thicker tome published many years ago: Penrose’s book, The Road to Reality. Like Penrose, Lewis presents a road map for the aspiring physicist. The plain English narrative offers something that is sorely absent from many textbooks: background and motivation. The technical appendices in turn make the connection between the core ideas and their actual implementation. And this is where the brevity of Lewis’s book might actually be an asset: Whereas Penrose spends several hundred pages discussing mostly pure mathematics, Lewis jumps right ahead into the physics.
So no, you will not learn general relativity or quantum field theory, nor the necessary mathematical foundations, from this book. But if you want to learn these subjects, the book can serve as your guide. Reading it before you dig into a textbook like Wald’s General Relativity of Peskin & Schroeder’s An Introduction to Quantum Field Theory will help maintain a bird’s eye perspective as you begin your journey. You may not have skills level-knowledge yet, but Lewis’s book will help you not lose sight of your intended destination as you study.
Let’s face it: These subjects are hard. Any resource that helps make it a tad easier to learn is welcome. And Lewis’s book definitely helps.
I cannot stop laughing.
Earlier today, I came across one of the weirdest papers yet that I’ve ever come across in the scientific literature.
I admit that my first thought was that it was a joke paper in a predatory journal. But no. It was a serious publication, in a serious journal, published under the Springer Nature label, no less.
And like all proper scientific publications, it had a title, an abstract, and… No, wait. It did not have an abstract. What it had instead was…
A pumping elephant.
Seriously. A pumping elephant.
But if it was not a joke paper, then what was it? Having noticed that the paper’s authors were all Chinese, it occurred to me that perhaps it’s a mistranslation. The AI Claude quickly confirmed my suspicion. Apparently, the authors mistranslated “Abstract” as “抽象” (chōuxiàng) in Chinese, which does mean “abstract” but in the sense of “abstract concept” rather than “summary of a paper”. They then literally translated 抽 (chōu), which can mean “to pump” and 象 (xiàng), which can mean “elephant”.
So perhaps it was an embarrassing but ultimately innocent mistake by the paper’s authors.
The same cannot be said about the journal’s editorial staff. That such a glaring piece of nonsense made it to the pages of a reputable journal signals a complete lack of copy-editing and editorial supervision.
To their credit, the paper was ultimately retracted. And it only took about three and a half years…
I asked Midjourney to create for me a pumping elephant. Clearly inspired by Verne’s famous novel, The Steam House, Midjourney produced some wonderful steampunk pumping elephants. This is my favorite so far.

Incidentally, there are also YouTube videos of bona fide pumping elephants: Elephants that learned to use a water pump.
Needless to say, I’ll be sorely tempted to use “Pumping elephant” to label the Abstract in my future publications…
I just made up my mind.
I’ll never again respond to unsolicited theories, unsolicited requests to comment, not even from Nobel-prize winners.
Because in the end, unless I enthusiastically agree with their ideas, no matter how silly, how outlandish, it always ends badly.
It doesn’t matter how polite I am, how carefully I choose my words, how much I try my darnedest to steer them in the right direction. And it makes no difference if the person in question is just, say, a taxi driver somewhere in Asia or an accomplished scientist in Europe.
If you have a scientific idea, do the right thing: write it up, send it to a journal, publish it. I am officially not interested anymore. Sorry, but I’ve been insulted one too many times and finally, my fuse got blown. I have better things to do than nursing your hurt feelings because the science community is not treating you seriously.

In fact, chances are that in the future, I’ll blacklist all such e-mail addresses right away. My sanity is more important than your feelings.
\(\renewcommand{\vec}[1]{\boldsymbol{\mathrm{#1}}}\)This is probably my most ambitious paper to date. It’d be a lie to suggest that I was not worried: what am I missing?
Which is why I have to begin by showing my appreciation to the editors of Classical and Quantum Gravity who, rather than dismissing my paper, recognized its potential value and invited no fewer than four reviewers. Much to my (considerable) relief the reviewers seemed to agree: What I am doing makes some sense.

One of my cats, helping me to understand gravity.
What exactly am I doing? Well, as everyone (ok, everyone with at least a casual interest in general relativity) knows, the gravitational field doubles as the metric of spacetime. And we know that the metric is a “symmetric” quantity: the distance from \(A\) to \(B\) is the same as the distance from \(B\) to \(A,\) and this does not change even when the “distance” in question is the spacetime interval, the infinitesimal proper time between neighboring events.
So we treat the metric as symmetric, which greatly simplifies calculations.
Alternatively, we may treat the metric as not symmetric. Einstein spent the last several decades of his life working on a theory using a nonsymmetric metric, which, he hoped, could have led to a unification of the theories of gravitation and electromagnetism. It didn’t.
John Moffat also spent a considerable chunk of his professional life working on his nonsymmetric gravitational theory (NGT). Unlike Einstein, Moffat assumed that the extra degrees of freedom are also gravitational and may lead to a large-scale modification of the expression for gravitational acceleration, potentially explaining riddles like the rotation curves of galaxies.
But herein lies the puzzle. A self-respecting field theory these days is usually written down by way of a Lagrangian density, with the corresponding field equations derived using the so-called action principle. In the case of general relativity, this Lagrangian density is called the Einstein-Hilbert Lagrangian. The field that is the subject of this Lagrangian is the gravitational field. Unless we are interested in Einstein’s unified field theory or Moffat’s NGT, we assume that this field has the requisite symmetry that is characteristic of a metric.
Except that at no point do we actually inform the machinery behind the action principle, namely the methods of the calculus of variations, that the field has this property. Rather, in standard derivations we just impose this constraint “by hand” during the derivation itself. This approach is mathematically inconsistent even if it leads to the desired, expected result.
Usually, a restriction that constrains the degrees of freedom of a physical system is incorporated into the Lagrangian using what are called Lagrange-multipliers. Why would we not use a Lagrange-multiplier, then, to restrict the gravitational field tensor so that instead of the 16 independent degrees of freedom that characterize a generic rank-2 tensor in four dimensions, we only have the 10 degrees of freedom of a symmetric tensor?
This is precisely what I have done. Not without consternation: After all, no lesser a mathematician than David Hilbert chose not to do this, even though he was very much aware of the technique of Lagrange-multipliers and their utility, which he took advantage of in other contexts while working on relativity theory.
Yet, for 109 years and counting, the symmetry of the metric, though assumed, was never incorporated into the standard Lagrangian formulation of the theory. I honestly don’t know why, but I decided to address this by introducing a Lagrange multiplier term:
\begin{align}
{\cal S}_{\rm grav}=\frac{1}{2\kappa}\int d^4x \sqrt{-g}(R-2\Lambda+\lambda^{\mu\nu}g_{[\mu\nu]}).
\end{align}
There. Variation with respect to this nondynamical term \(\lambda^{\mu\nu}\) yields the constraint, \(g_{[\mu\nu]}=0\). Job done. Except… Except that as a result of introducing this term, Einstein’s field equations are slightly modified, split into two equations as a matter of fact:
\begin{align}
R_{\mu\nu}-\tfrac{1}{2}Rg_{\mu\nu}+\Lambda g_{\mu\nu} &{}= 8\pi G T_{(\mu\nu)},\\
\lambda_{[\mu\nu]} &{}= 8\pi GT_{[\mu\nu]}.
\end{align}
The first of these two equations is just the usual field equation, but with a twist: The stress-energy tensor on the right-hand side is explicitly symmetrized.
But the second! That’s where things get really interesting. The nondynamical term \(\lambda_{[\mu\nu]}\) is unconstrained. That means that the antisymmetric part of \(T_{\mu\nu}\) can be anything. To quote a highlighted sentence from my own manuscript: “Einstein’s gravitational field is unaffected by the antisymmetric part of a generalized stress-energy-momentum tensor.“
Or, to put it more bluntly, the gravitational field does not give a flying fig about matter spinning or rotating. How matter spins or does not spin would be determined by the properties of that matter; gravity does not care.
This was a surprising, potentially profound result. Previously, authors tried to account for the presence of nonvanishing rotation by introducing a variety of tensor formalisms ad hoc. But as my derivation shows, perhaps all that was unnecessary. Matter is free to rotate, insofar as gravity is concerned: the stress-energy tensor does not need to be symmetrical.
Is this result really new? How can that be? What am I missing? These were my thoughts when I submitted my manuscript. Who knows… maybe, just maybe I was not spouting nonsense and stumbled upon something of real importance.
I expect my paper to appear on the pages of CQG in due course [edit: it just did]; I now also submitted the manuscript to arXiv, where it should appear I hope this weekend or early next week.
For many years now, I’ve been receiving regular invitations from low-quality, predatory journals to contribute papers.
Needless to say, I didn’t.
But today, it reached a new low. I was offered, in exchange for the princely sum of $30, “authorship positions” in any one of a set of 19 papers.
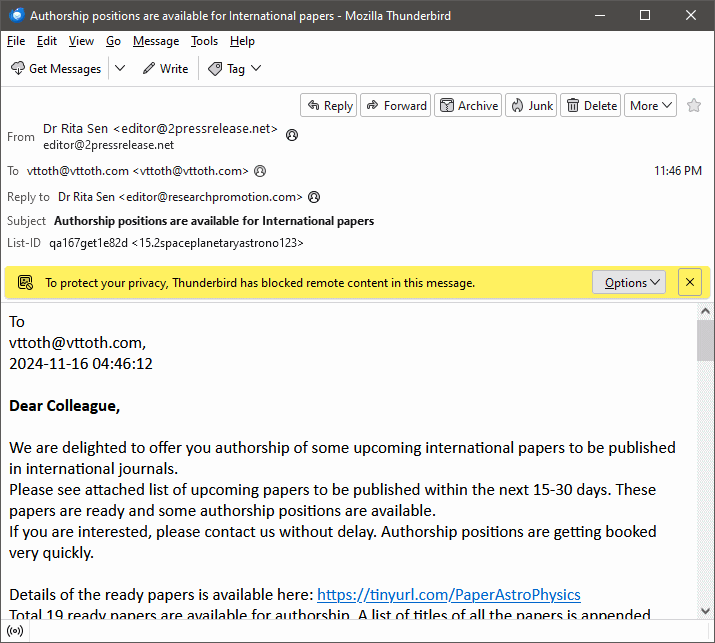
Holy macaroni. Or whatever.
The esteemed journal in question that is inviting me to throw away any semblance of scientific ethics just to have my name appear… somewhere, calls itself the International Astronomy and Astrophysics Research Journal. Several paragraphs later in the e-mail I learn the…
List of Ready Paper
1. Advances in Dark Energy Research: Understanding the Mystery of the Accelerating Universe
2. Progress in Dark Matter Research: Bridging Observations and Theoretical Insights
3. A Review on Advances in Gravitational Waves Research
4. Recent Advances in the Cosmic Microwave Background Research: A Review
5. Galaxy Formation and Evolution: Progress in Recent Research
6. Computational Astrophysics Research: Review of the Recent Progress and Future Directions
7. Heavy-Ion Studies Research: Current Progress and Future Directions
8. Advances and Future Directions in Cosmic Ray Research: A Comprehensive Review
9. Gravitational Lensing: Review of Recent Progress and Future Directions
10. Advances in Black Hole Research and Future Directions: A Review
11. Exoplanet: Recent Developments and Future Directions: A Review
12. Recent Advances in Galaxy Formation Research and Future Developments
13. Galaxy Clusters: A comprehensive Review of Recent Developments
14. Recent Advances and Future Directions of Solar Physics Research
15. Recent Advances in Astrophysical Magnetism and the Interstellar Medium Research
16. A Review of Interstellar Black Holes: Navigating the Invisible
17. Recent Advances in Star Formation Theories: A Comprehensive Review
18. A Review of Recent Progress in Supermassive Black Holes and Galaxy Formation Research
19. Advances in Neutron Stars and Pulsars Research: Recent Progress and Future Directions
Yes, I’ve said it before, scientific publishing is in a crisis: flooded with low quality research, in need of qualified reviewers, stuck between two contradictory business models (subscription-based vs. open access publishing) and facing a deluge of for-profit, predatory publishers. But this represents a new low even within that dismal landscape.
Overleaf (sharelatex) is an amazing project, an open-source Web-based editor for LaTeX projects. The software can be used for free or on a subscription basis at overleaf.com, but the open source version is available as a “community edition”.
Not for the faint-hearted, mind you, as installation is not trivial. The easiest way is by means of a docker container, setup for which is provided by the Overleaf project.
In the last few days, I managed to do just that, installing Overleaf on my main Linux server. I even managed to configure Overleaf to properly compile Feynman diagrams automatically, as this screenshot from my practice “scratchpad” file demonstrates.
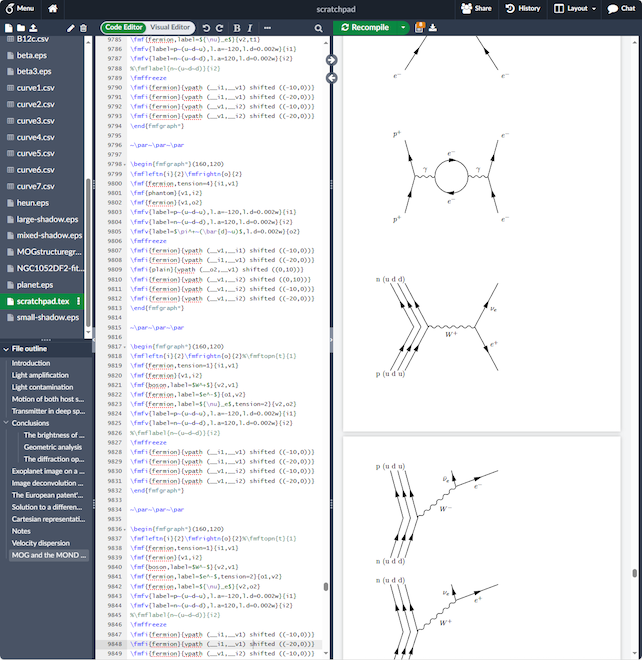
I like this project very much. In fact I am very impressed by its sophistication. I first opened an Overleaf account more than six years ago, when I invited someone to collaborate. I used Overleaf a few times over the years but, I admit, I forgot that it even exists until recently, when someone invited me to collaborate and I found, much to my surprise, that I already had a valid Overleaf account.
But this time around I went far beyond just using it. I decided to set up my own installation, for several reasons, including privacy, confidentiality, limitations and last but not least, avoiding reliance of a service provider who may or may not be still in business tomorrow or next year.
And now, I find myself ready to ditch the old software that I’ve been using for nearly 20 years, and switch to Overleaf altogether for my new LaTeX projects. It’s that good, really. I hope I will not come to regret my decision.
Starliner, made it safely to the ground, albeit without its crew.

Whatever unkind thoughts I have towards Boeing these days, this is good news.
It’s a civic holiday Monday that feels like a Saturday, reminding me of an old Soviet-era science-fiction novel, Monday begins on Saturday, by the Strugatsky brothers. It’s also a rather gloomy Monday morning, so it’s time for me to grumble about a few things.
For instance, how politics infuses everything these days. I signed up to follow a Facebook group dedicated to brutalist architecture, which for some inexplicable reason, I like. The comments section in one of the first posts I saw rapidly deteriorated into political bickering, as to whether or not it was appropriate to repurpose one of the Nazi-era indestructible flak towers in Hamburg as a luxury hotel. Because you know, politics is everything.

Speaking of which, I saw another post elsewhere about employees of a large US company who, after being told how successful the company was last year, were informed in the same breath that the company will cut their pension plan contributions. Needless to say, there followed comments about the evils of capitalism. Having experienced both capitalism and one of its alternatives, a socialist economy with central planning, all I can say is that capitalism works most of the time until it doesn’t; but when it doesn’t, victims are ever so eager to replace it with something that never works instead.
Then there was this post at an online news site claiming that it is practically impossible to run an ethical AI company. Well, what can I say? If you are telling me that allowing machine learning algorithms to learn from accumulated human knowledge is unethical, then sure, you are absolutely right. Then again, I suspect that what mainly drives such complaints is blatant ignorance of how machine learning works in the first place.
OK, well, never mind that, there’s good news. A fusion energy breakthrough: Neutron impact on tokamak components uncovered. Er… Say again? You are telling me that after 70+ years of research, we are beginning to understand why, or how, a heavy neutron flux rapidly destroys test equipment in the lab? Isn’t that like, say, greeting it as a “steam turbine breakthrough” when a prehistoric tribe manages to draw a spark from slamming together two rocks?
Oh well. On mornings like this, I feel I am beginning to comprehend the mood of the late, great Kurt Vonnegut who once told the CBC’s Anna Maria Tremonti to go jump in a lake.
The title of this blog post is used as the byline or catch phrase of the Canadian Centre for Experimental Radio Astronomy, a group operating a 12.8 meter radio telescope, a repurposed former NATO satellite communication facility, located in Carp, just outside of Ottawa.
One of the things they organize is a summer camp for students. Today, I was invited to talk to a small group of students, and indeed I did so, talking (mostly) about my work on the Pioneer Anomaly. It seemed like an appropriate topic, considering that detection and resolution of the anomaly was heavily dependent on radio science, specifically Doppler radio navigation.
It was fun, and my talk, I am told, was well received. I was also offered an opportunity to briefly tour the facility itself. It was fascinating, even though it was insanely hot inside the dome under the August sun. (I definitely needed a shower when I got back home.) The only memorable fly in the proverbial ointment is that I arrived late, thanks to a stupid disabled truck that blocked the Queensway, as a result of which it took forty minutes to get from Vanier Parkway to Parkdale. Fortunately, my hosts were understanding.