My blog is supposed to be (mostly) about physics. So let me write something about physics for a change.
John Moffat, with whom I have been collaborating (mostly on his modified gravity theory, MOG) for the past six years or so, has many ideas. Recently, he was wondering: could the celebrated 125 GeV (125 gigaelectronvolts divided the speed of light squared, to be precise, which is about about 134 times the mass of a hydrogen atom) peak observed last year at the LHC (and if rumors are to be believed, perhaps to be confirmed next week) be a sign of something other than the Higgs particle?
All popular accounts emphasize the role of the Higgs particle in making particles massive. This is a bit misleading. For one thing, the Higgs mechanism is directly responsible for the masses of only some particles (the vector bosons); for another, even this part of the mechanism requires that, in addition to the Higgs particle, we also presume the existence of a potential field (the famous “Mexican hat” potential) that is responsible for spontaneous symmetry breaking.
Higgs mechanism aside though, the Standard Model of particle physics needs the Higgs particle. Without the Higgs, the Standard Model is not renormalizable; its predictions diverge into meaningless infinities.
The Higgs particle solves this problem by “eating up” the last misbehaving bits of the Standard Model that cannot be eliminated by other means. The theory is then complete: although it remains unreconciled with gravity, it successfully unites the other three forces and all known particles into a unified (albeit somewhat messy) whole. The theory’s predictions are fully in accordance with data that include laboratory experiments as well as astrophysical observations.
Well, almost. There is still this pesky business with neutrinos. Neutrinos in the Standard Model are massless. Since the 1980s, however, we had strong reasons to suspect that neutrinos have mass. The reason is the “solar neutrino problem”, a discrepancy between the predicted and observed number of neutrinos originating from the inner core of the Sun. This problem is resolved if different types of neutrinos can turn into one another, since the detectors in question could only “see” electron neutrinos. This “neutrino flavor mixing” or “neutrino oscillation” can occur if neutrinos have mass, represented by a mass matrix that is not completely diagonal.
What’s wrong with introducing such a matrix, one might ask? Two things. First, this matrix necessarily contains dimensionless quantities that are very small. While there is no a priori reason to reject them, dimensionless numbers in a theory that are orders of magnitude bigger or smaller than 1 are always suspect. But the second problem is perhaps the bigger one: massive neutrinos make the Standard Model non-renormalizable again. This can only be resolved by either exotic mechanisms or the introduction of new elementary particles.
This challenge to the Standard Model perhaps makes the finding of the Higgs particle less imperative. Far from turning a nearly flawless theory into a perfect one, it only addresses some problems in an otherwise still flawed, incomplete theory. Conversely, not finding the Higgs particle is less devastating: it does invalidate a theory that would have been perfect otherwise, it simply prompts us to look for solutions elsewhere.
In light of that, one may wish to take a second look at the observations reported at the LHC last fall. The Higgs particle, if it exists, can decay in several ways. We already know that the Higgs particle cannot be heavier than 130 GeV, and this excludes certain forms of decay. One of the decays that remains is the decay into a quark and its antiparticle that, in turn, decay into two photons. Photons are easy to observe, but there is a catch: when the LHC collides large numbers of protons with one another at high energies, a huge number of photons are created as a background. It is against this background that two-photon events with a signature specific to the Higgs particle must be observed.
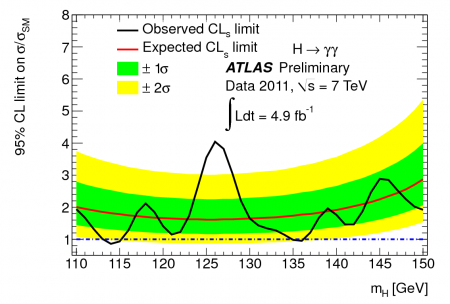
Diphoton results from the Atlas detector at the LHC, late 2011.
And observed they have been, albeit not with a resounding statistical significance. There is a small excess of such two-photon events indicating a possible Higgs mass of 125 GeV. Many believe that this is because there is indeed a Higgs particle with this mass, and its discovery will be confirmed with the necessary statistical certainty once more data are collected.
Others remain skeptical. For one thing, that 125 GeV peak is not the only peak in the data. For another, it is a peak that is a tad more pronounced than what the Higgs particle would produce. Furthermore, there is no corresponding peak in other “channels” that would correspond to other forms of decay of the Higgs particle.
This is when Moffat’s idea comes in. John had in mind the many “hadronic resonances”, all sorts of combinations of quarks that appear at lower energies, some of which still befuddle particle physicists. What if, he asks, this 125 GeV peak is due to just another such resonance?
Easier said than done. At low energies, there are plenty of quarks to choose from and combine. But 125 GeV is not a very convenient energy from this perspective. The heaviest quark, the top quark has a mass of 173 GeV or so; far too heavy for this purpose. The next quark in terms of mass, the bottom quark, is much too light at around 4.5 Gev. There is no obvious way to combine a reasonably small number of quarks into a 125 GeV composite particle that sticks around long enough for it to be detected. Indeed, the top quark is so heavy that “toponium”, a hypothetical combination of a top quark and its antiparticle, is believed to be undetectable; it decays so rapidly, it really never has time to form in the first place.
But then, there is another possibility. Remember how neutrinos oscillate between different states? Well, composite particles can do that, too. And as to what these “eigenstates” are, that really depends on the measurement. One notorious example is the neutral kaon (also known as the neutral K meson). It has one eigenstate with respect to the strong interaction, but two quite different eigenstates with respect to the weak interaction.
So here is John’s perhaps not so outlandish proposal: what if there is a form of quarkonium whose eigenstates are toponium (not observed) and bottomonium with respect to some interactions, but two different mixed states with respect to whatever interaction is responsible for the 125 GeV resonance observed by the LHC?
Such an eigenstate requires a mixing angle, easily calculated as 20 degrees. This mixing also results in another eigenstate, at 330 GeV, which is likely so heavy that it is not stable enough to be observed. This proposal, if valid, would explain why the LHC sees a resonance at 125 GeV without a Higgs particle.
Indeed, this proposal can also explain a) why the peak is stronger than what one would predict for the Higgs particle, b) why no other Higgs-specific decay modes were observed, and perhaps most intriguingly, c) why there are additional peaks in the data!
That is because if there is a “ground state”, there are also excited states, the same way a hydrogen atom (to use a more commonplace example) has a ground state and excited states with its lone electron in higher energy orbits. These excited states would show up in the plots as additional resonances, usually closely bunched together, with decreasing magnitude.
Could John be right? I certainly like his proposal, though I am not exactly the unbiased observer, since I did contribute a little to its development through numerous discussions. In any case, we will know a little more next week. An announcement from the LHC is expected on July 4. It is going to be interesting.