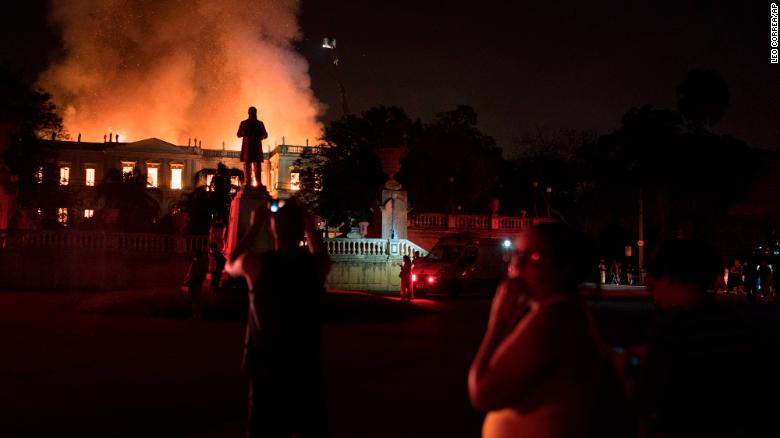Years ago, I accepted the role of release manager for the Maxima computer algebra system. It proved to be more laborious than I assumed (mostly for two things: assembling changelogs, and dealing with build glitches) but it still has its upside. Right now, it is my pleasure to announce that Maxima 5.42 has been released on the unsuspecting public. Enjoy!
Michael Atiyah, 89, is one of the greatest living mathematicians. Which is why the world pays attention when he claims to have solved what is perhaps the greatest outstanding problem in mathematics, the Riemann hypothesis.
Here is a simple sum: \(1+\frac{1}{2^2}+\frac{1}{3^2}+…\). It is actually convergent: The result is \(\pi^2/6\).
Other, similar sums also converge, so long as the exponent is greater than 1. In fact, we can define a function:
$$\begin{align*}\zeta(x)=\sum\limits_{i=1}^\infty\frac{1}{i^x}.\end{align*}$$
Where things get really interesting is when we extend the definition of this \(\zeta(x)\) to the entire complex plane. As it turns out, its analytic continuation is defined almost everywhere. And, it has a few zeros, i.e., values of \(x\) for which \(\zeta(x)=0\).
The so-called trivial zeros of \(\zeta(x)\) are the negative even integers: \(x=-2,-4,-6,…\). But the function also has infinitely many nontrivial zeros, where \(x\) is complex. And here is the thing: The real part of all known nontrivial zeros happens to be \(\frac{1}{2}\), the first one being at \(x=\frac{1}{2}+14.1347251417347i\). This, then, is the Riemann hypothesis: Namely that if \(x\) is a non-trivial zero of \(\zeta(x)\), then \(\Re(x)=\frac{1}{2}\). This hypothesis baffled mathematicians for the past 130 years, and now Atiyah claims to have solved it, accidentally (!), in a mere five pages. Unfortunately, verifying his proof is above my pay grade, as it references other concepts that I would have to learn first. But it is understandable why the mathematical community is skeptical (to say the least).

A slide from Atiyah’s talk on September 24, 2018.
What is not above my pay grade is analyzing Atiyah’s other claim: a purported mathematical definition of the fine structure constant \(\alpha\). The modern definition of \(\alpha\) relates this number to the electron charge \(e\): \(\alpha=e^2/4\pi\epsilon_0\hbar c\), where \(\epsilon_0\) is the electric permeability of the vacuum, \(\hbar\) is the reduced Planck constant and \(c\) is the speed of light. Back in the days of Arthur Eddington, it seemed that \(\alpha\sim 1/136\), which led Eddington himself onto a futile quest of numerology, trying to concoct a reason why \(136\) is a special number. Today, we know the value of \(\alpha\) a little better: \(\alpha^{-1}\simeq 137.0359992\).
Atiyah produced a long and somewhat rambling paper that fundamentally boils down to two equations. First, he defines a new mathematical constant, denoted by the Cyrillic letter \(\unicode{x427}\) (Che), which is related to the fine structure constant by the equation
$$\begin{align*}\alpha^{-1}=\frac{\pi\unicode{x427}}{\gamma},\tag{1.1*}\end{align*}$$
where \(\gamma=0.577…\) is the Euler–Mascheroni constant. Second, he offers a definition for \(\unicode{x427}\):
$$\begin{align*}\unicode{x427}=\frac{1}{2}\sum\limits_{j=1}^\infty 2^{-j}\left(1-\int_{1/j}^j\log_2 x~dx\right).\tag{7.1*}\end{align*}$$
(The equation numbers are Atiyah’s; I used a star to signify that I slightly simplified them.)
Atiyah claims that this sum is difficult to calculate and then goes into a long-winded and not very well explained derivation. But the sum is not difficult to calculate. In fact, I can calculate it with ease as the definite integral under the summation sign is trivial:
$$\begin{align*}\int_{1/j}^j\log_2 x~dx=\frac{(j^2+1)\log j-j^2+1}{j\log 2}.\end{align*}$$
After this, the sum rapidly converges, as this little bit of Maxima code demonstrates (NB: for \(j=1\) the integral is trivial as the integration limits collapse):
(%i1) assume(j>1);
(%o1) [j > 1]
(%i2) S:1/2*2^(-j)*(1-integrate(log(x)/log(2),x,1/j,j));
log(j) + 1
---------- + j log(j) - j
(- j) - 1 j
(%o2) 2 (1 - -------------------------)
log(2)
(%i3) float(sum(S,j,1,50));
(%o3) 0.02944508691740671
(%i4) float(sum(S,j,1,100));
(%o4) 0.02944508691730876
(%i5) float(sum(S,j,1,150));
(%o5) 0.02944508691730876
(%i6) float(sum(S,j,1,100)*%pi/%gamma);
(%o6) 0.1602598029967022
Unfortunately, this does not look like \(\alpha^{-1}=137.0359992\) at all. Not even remotely.
So we are all left to guess, sadly, what Atiyah was thinking when he offered this proposal.
We must also remember that \(\alpha\) is a so-called “running” constant, as its value depends on the energy of the interaction, though presumably, the constant in question here is \(\alpha\) in the infrared limit, i.e., at zero energy.
There is a white rabbit who set up residence near my wife’s allotment garden.

This is obviously not a wild animal. He may be okay for now, but for how long? How long before either a predator finishes it off, or bad weather sets in?
In short, I think it needs a home. I have no idea what to do with a rabbit and we have two cats already. But perhaps a good soul sees this post…
Outraged over ever increasing phone bills, today I decided to cancel our second landline.
We used to use this line a fair deal. It was, back in the days of dial-up modems, my phone line for incoming dial-up calls (e.g., when I was traveling) and also a means to maintain a backup, low-speed Internet connection. It was occasionally used by my wife, as it was the line to which a dual-mode Skype-and-landline phone was connected.
And, of course, it was used for that miracle of 20th century technology: facsimile transmissions.

Of course, this is 2018 now, and I have not used a dial-up data connection in at least a decade. No travel computer of mine had a modem, in fact, since the early 2000s. My old travel kit, containing various country-specific phone plugs, even a screwdriver and alligator clips, lies on a shelf, forgotten. And Skype? Microsoft betrayed many Skype users, myself included, when they irreversibly changed the Skype protocol, rendering old Skype-compatible hardware useless. Yes, I feel a bit bitter about it… I liked that Skype phone, I even fixed it once when its original microphone died and had to be replaced. Now it’s just another worthless piece of junk electronics. And once the Skype phone was no longer useful for, well, Skype, my wife also stopped using it as a landline phone, opting instead to use her mobile phone for local calls.
As for faxes… How quaint. Faxes. When was the last time you sent a fax? Or received one? I cannot remember.
To make a long story short, this second line has remained pretty much unused for the past year or two. Yet Bell kept ratcheting up the price. My most recent monthly phone bill for the two landlines reached $125, and that’s where I decided to draw the line. I called up Bell in the hope that they might have a decent offer for a long-time customer but no, nothing. In fact, it almost felt as if they wanted me to get rid of that second line. (Makes you wonder what the hell is going on there.) So… the second line has been terminated.
Well, supposedly anyway. It was at least six hours ago that Bell told me that the line would be deactivated within 15-120 minutes… but it still gives a dial tone, and I can still ring it. Go figure. I suspect the line will be dead tomorrow anyway.
OK, so we’ve had Trump for nearly two years now, and we know that the White House has become a combination of kindergarten and insane asylum. My conservative friends still support Trump because he “delivers”, and are willing to completely overlook the fact that this president is not only a bumbling dilettante, an offensive excuse of a human being (waste of skin, to borrow a phrase from Lexx, a science-fiction series from a few years ago) but quite possibly a traitor to his nation, too, working for Putin’s Russia.

But if I hoped that Trump’s opposition is any better, they bitterly disappoint each and every day.
Take, for instance, the made-up controversy of a Kavanaugh aide presumably flashing “white power” hand signs while sitting behind Kavanaugh during his Supreme Court hearing, visible to cameras. Never mind that the hand sign was, in fact, a perfectly ordinary OK sign. Never mind that it was a well-documented Internet hoax from last year that suggested that this OK sign is, in fact, a secret hand gesture used by white supremacists. None of that stops many of my liberal friends from tweeting and retweeting the meme, complete with obscenities and death threats. Fact checking is for wimps, I guess.
And now I am reading about the bitter fate of a paper exploring the mathematics behind a controversial hypothesis dating back to Darwin’s times, called the “Greater Male Variability Hypothesis” (GMVH). The GMVH basically asserts that there are more idiots and more geniuses among men than women. It was Darwin who first noted that such greater variability is prevalent across many species in the animal kingdom. But politically correct guardians of science publishing would have none of that. Poor Darwin… the right hates him because he dares to challenge the idea that the world was created 6,000 years ago, but now the left hates him, too, because he dares to offer us politically incorrect science. The paper by Theodore P. Hill was first accepted and then rejected by journals, including a journal that already published the paper online, only to replace it with another a few days later. Never even mind the attack on academic freedom that this represents, but how about blatant sexism? You know, those impressionable young female scientists, fragile little flowers that they are, who cannot handle scientific truth and must be protected at all costs, unlike their ever so manly male colleagues…
One of the guests on Fareed Zakaria’s show today on CNN was Jonathan Haidt, one of the authors of the book, The Coddling of the American Mind. The authors explore the consequences of what they dub “safetyism”: Keeping children away from danger, real or perceived, at all costs, thus denying them a chance to become independent human beings. The result, according to the book, is that rates of anxiety, depression, even suicide are rising at an alarming rate, even as both students and professors on college campuses walk on eggshells, less they offend someone with a careless word, or heaven forbid, a hand gesture…
All in all, I am ready to conclude that the world is going bonkers, and those who seek salvation from Trump’s political opposition on the left (or seek salvation left-wing political opposition to right-wing populism and nativism elsewhere in the world) are deluding themselves.
Regardless of what I think of Trump’s dilettantism, adventurism or downright treasonous behavior, two wrongs do not make a right.
Anonymous senior officials secretly sabotaging the duly elected president? That is a cure that may be much worse than the disease. It amounts to no less than a bloodless coup.

Yes, I purposefully included a picture of Trump’s inauguration as a reminder that, for all his shenanigans, he is the duly elected president. There are constitutional means to remove a president through impeachment or through the 25th Amendment. The constitution, as far as I know, does not entitle anonymous, unelected officials, no matter how well-intentioned, to sabotage a president. That creates a precedent that is far worse than Trump’s incompetence or even (if my suspicions are proven true) treasonous behavior.
This tragic piece of news from this weekend escaped my attention. Brazil’s National Museum and its collection of some 20 million artifacts, going up in flames in a devastating fire.
And it’s not just artifacts. One thing mentioned was irreplaceable written and audio records, which likely have not yet been digitized, of indigenous languages no longer spoken.
The scale of devastation becomes clear from aerial photos, which show that almost nothing remained between the building’s exterior walls.

It is almost incomprehensible that such a disaster could take place in a national museum. The loss… it’s beyond belief.