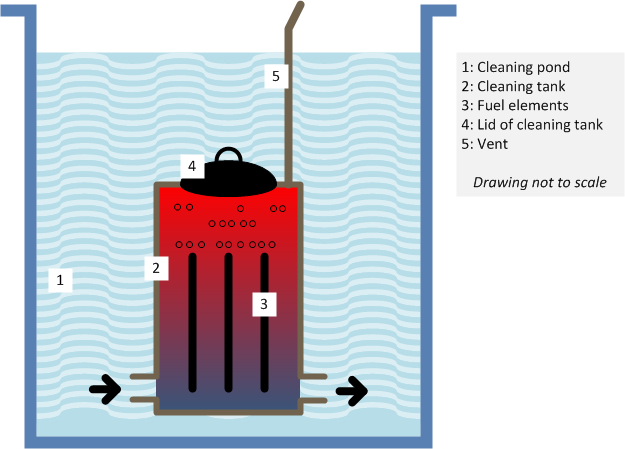
I have some half-baked ideas about the foundations of quantum physics (okay, who doesn’t.) When I say half-baked, I don’t mean that they are stupid (I sure hope not!) I simply mean I am not 100% sure about them, and there is more to learn.
I have some half-baked ideas about the foundations of quantum physics (okay, who doesn’t.) When I say half-baked, I don’t mean that they are stupid (I sure hope not!) I simply mean I am not 100% sure about them, and there is more to learn.
But, I am allowed to have opinions. So when I came across this informal 2013 poll among (mostly) quantum physicists, I decided to answer the questions myself.
Question 1: What is your opinion about the randomness of individual quantum events (such as the decay of a radioactive atom)?
a. The randomness is only apparent: 9%
b. There is a hidden determinism: 0%
c. The randomness is irreducible: 48%
d. Randomness is a fundamental concept in nature: 64%
(“Jedenfalls bin ich überzeugt, daß [der Alte] nicht würfelt.”)
Question 2: Do you believe that physical objects have their properties well defined prior to and independent of measurement?
a. Yes, in all cases: 3%
b. Yes, in some cases: 52%
c. No: 48%
d. I’m undecided: 9%
(Note that the question does not say that “well-defined” is a synonym for “in an eigenstate”.)
Question 3: Einstein’s view of quantum mechanics
a. Is correct: 0%
b. Is wrong: 64%
c. Will ultimately turn out to be correct: 6%
d. Will ultimately turn out to be wrong: 12%
e. We’ll have to wait and see: 12%
(Einstein’s views are dated, but I feel that he may nonetheless be vindicated because his reasons for holding those views would turn out to be valid. But, we’ll have to wait and see.)
Question 4: Bohr’s view of quantum mechanics
a. Is correct: 21%
b. Is wrong: 27%
c. Will ultimately turn out to be correct: 9%
d. Will ultimately turn out to be wrong: 3%
e. We’ll have to wait and see: 30%
(If I said “wait and see” on Einstein’s views, how could I possibly answer this question differently?)
Question 5: The measurement problem
a. A pseudoproblem: 27%
b. Solved by decoherence: 15%
c. Solved/will be solved in another way: 39%
d. A severe difficulty threatening quantum mechanics: 24%
e. None of the above: 27%
(Of course it’s a pseudoproblem. It vanishes the moment you look at the whole world as a quantum world.)
Question 6: What is the message of the observed violations of Bell’s inequalities?
a. Local realism is untenable: 64%
b. Action-at-a-distance in the physical world: 12%
c. Some notion of nonlocality: 36%
d. Unperformed measurements have no results: 52%
e. Let’s not jump the gun—let’s take the loopholes more seriously: 6%
(I don’t like how the phrase “local realism” is essentially conflated with classical eigenstates. Why is a quantum state not real?)
Question 7: What about quantum information?
a. It’s a breath of fresh air for quantum foundations: 76%
b. It’s useful for applications but of no relevance to quantum foundations: 6%
c. It’s neither useful nor fundamentally relevant: 6%
d. We’ll need to wait and see: 27%
(I wish there was another option: e. A fad. Then again, it does have some practical utility, so b is my answer.)
Question 8: When will we have a working and useful quantum computer?
a. Within 10 years: 9%
d. In 10 to 25 years: 42%
c. In 25 to 50 years: 30%
d. In 50 to 100 years: 0%
e. Never: 15%
(The threshold theorem supposedly tells us what it takes to avoid decoherence. What I think it tells us is the limits of quantum error correction and why decoherence is unavoidable.)
Question 9: What interpretation of quantum states do you prefer?
a. Epistemic/informational: 27%
b. Ontic: 24%
c. A mix of epistemic and ontic: 33%
d. Purely statistical (e.g., ensemble interpretation): 3%
e. Other: 12%
(Big words look-up time, but yes, ontic it is. I may have remembered the meaning of “ontological”, but I nonetheless would have looked up both, just to be sure that I actually understand how these terms are used in the quantum physics context.)
Question 10: The observer
a. Is a complex (quantum) system: 39%
b. Should play no fundamental role whatsoever: 21%
c. Plays a fundamental role in the application of the formalism but plays no distinguished physical role: 55%
d. Plays a distinguished physical role (e.g., wave-function collapse by consciousness): 6%
(Of course the observer is a complex quantum system. I am surprised that some people still believe this new age quantum consciousness bull.)
Question 11: Reconstructions of quantum theory
a. Give useful insights and have superseded/will supersede the interpretation program: 15%
b. Give useful insights, but we still need interpretation: 45%
c. Cannot solve the problems of quantum foundations: 30%
d. Will lead to a new theory deeper than quantum mechanics: 27%
e. Don’t know: 12%
(OK, I had to look up the papers, as I had no recollection of the word “reconstruction” used in this context. As it turns out, I’ve seen papers in the past on this topic and they left me unimpressed. My feeling is that even as they purport to talk about quantum theory, what they actually talk about are (some of) its interpretations. And all too often, people who do this leave QFT completely out of the picture, even though it is a much more fundamental theory than single particle quantum mechanics!)
Question 12: What is your favorite interpretation of quantum mechanics?
a. Consistent histories: 0%
b. Copenhagen: 42%
c. De Broglie–Bohm: 0%
d. Everett (many worlds and/or many minds): 18%
e. Information-based/information-theoretical: 24%
f. Modal interpretation: 0%
g. Objective collapse (e.g., GRW, Penrose): 9%
h. Quantum Bayesianism: 6%
i. Relational quantum mechanics: 6%
j. Statistical (ensemble) interpretation: 0%
k. Transactional interpretation: 0%
l. Other: 12%
m. I have no preferred interpretation 12%
(OK, this is the big one: which camp is yours! And the poll authors themselves admit that it was a mistake to leave out n. Shut up and calculate. I am disturbed by the number of people who opted for Everett. Information-based interpretations seem to be the fad nowadays. I am surprised by the complete lack of support for the transactional interpretation, and also by the low level of support for Penrose. I put myself in the Other category, because my half-baked ideas don’t precisely fit into any of these boxes.)
Question 13: How often have you switched to a different interpretation?
a. Never: 33%
b. Once: 21%
c. Several times: 21%
d. I have no preferred interpretation: 21%
(I am not George W. Bush. I don’t “stay the course”. I change my mind when I learn new things.)
Question 14: How much is the choice of interpretation a matter of personal philosophical prejudice?
a. A lot: 58%
b. A little: 27%
c. Not at all: 15%
(I put my mark on a. because that’s the way it is today. If you asked me how it should be, I’d have answered c.)
Question 15: Superpositions of macroscopically distinct states
a. Are in principle possible: 67%
b. Will eventually be realized experimentally: 36%
c. Are in principle impossible: 12%
d. Are impossible due to a collapse theory: 6%
(Of course it’s a. Quantum physics is not about size, it’s about the number of independent degrees of freedom.)
Question 16: In 50 years, will we still have conferences devoted to quantum foundations?
a. Probably yes: 48%
b. Probably no: 15%
c. Who knows: 24%
d. I’ll organize one no matter what: 12%
(Probably yes but do I really care?)
OK, now that I answered these poll questions myself, does that make me smart? I don’t feel any smarter.

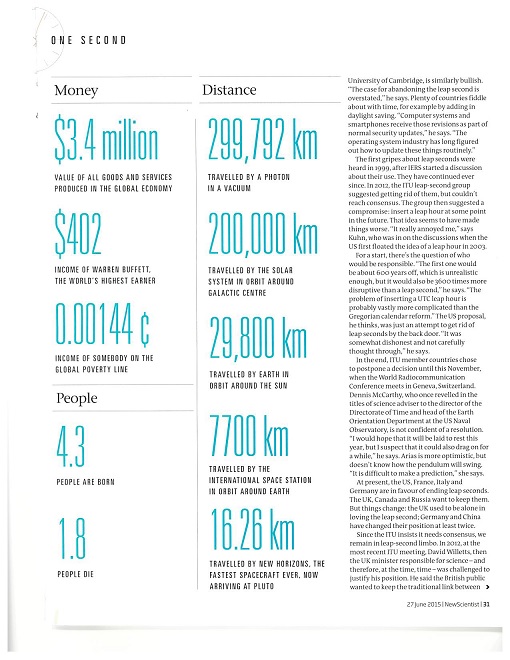






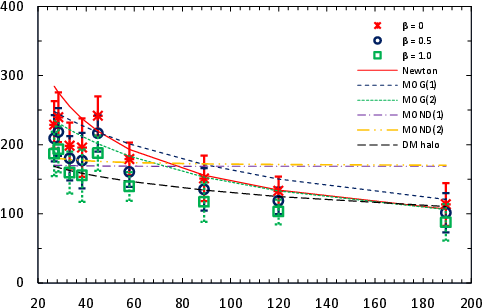
 I have some half-baked ideas about the foundations of quantum physics (okay, who doesn’t.) When I say half-baked, I don’t mean that they are stupid (I sure hope not!) I simply mean I am not 100% sure about them, and there is more to learn.
I have some half-baked ideas about the foundations of quantum physics (okay, who doesn’t.) When I say half-baked, I don’t mean that they are stupid (I sure hope not!) I simply mean I am not 100% sure about them, and there is more to learn.