Spinor Info

I don’t normally comment on crank science that finds its way into my Inbox, but this morning I got a really good laugh.

The announcement was dramatic enough: the e-mail bore the title, “Apparent detection of antimatter galaxies”. It came from the “Santilli foundation”, who sent me some eyebrow-raising e-mails in the past, but this was sufficiently intriguing to make me click on the link they provided. So click I did, only to be confronted with the following image:

What’s that, you ask? Why, a telescope with a concave lens. Had I paid a little bit more attention to the e-mail, I might have been a little less surprised; they did include a longer title, you see, helpfully typeset in all caps, which read, “APPARENT DETECTION OF ANTIMATTER GALAXIES VIA SANTILLI’S TELESCOPE WITH CONCAVE LENSES”.

Say what? Concave lenses? Why, it’s only logical. If light from an ordinary galaxy is focused by a convex lens, then surely, light from an antimatter galaxy will be focused by a concave lens. This puts this Santilli fellow in the same league as Galileo; like his counterpart five centuries ago, Santilli also invented his own telescope. But wait, Santilli is also a modern-day Newton: like Newton, he invented a whole new branch of mathematics, which he calls “isodual mathematics”. Certainly sounds impressive.

So what does Einstein’s relativity have to say about all this? Why, it’s all a “century of scientific scams by organized interests on Einstein […] to discredit opposing views”. It’s all “sheer dishonesty and scientific gangsterism”. But it is possible “for the United Stated of America to regain a minimum of international scientific credibility”. All that is needed is to “investigate the legality of the current use of public funds by the Department of Energy and the National Science Foundation on research based on the current mandate of compatibility with Einstein’s theory” and the US of A will cease to be bankrupt.

Oh, and you also need some telescopes with concave lenses.

I am reading a very interesting paper by Christian Beck, recently published in Physical Review Letters.

Beck revives the proposal that at least some of the as yet unobserved dark matter in the universe may be in the form of axions. But he goes further: he suggests that a decade-old experiment with superconducting Josephson-junctions that indicated the presence of a small, unexplained signal may in fact have been a de facto measurement of the axion background in our local galactic neighborhood.

If true, Beck’s suggestion has profound significance: not only would dark matter be observable, but it can be observed with ease, using a tabletop experiment!

What is an axion? The Standard Model of particle physics (for a very good comprehensive review, I recommend The Standard Model: A Primer by Cliff Burgess and Guy Moore, Cambridge University Press, 2007) can be thought of as the most general theory based on the observed particle content in the universe. By “most general”, I mean specifically that the Standard Model can be written in the form of a Lagrangian density, and all the terms that can be present do, in fact, correspond to physically observable phenomena.

All terms except one, that is. The term, which formally reads

\begin{align}{\cal L}_\Theta=\Theta_3\frac{g_3^2}{64\pi^2}\epsilon^{\mu\nu\lambda\beta}G^\alpha_{\mu\nu}G_{\alpha\lambda\beta},\end{align}

where \(G\) represents gluon fields and \(g_3\) is the strong coupling constant (\(\epsilon^{\mu\nu\lambda\beta}\) is the fully antisymmetric Levi-Civita pseudotensor), does not correspond to any known physical process. This term would be meaningless in classical physics, on account of the fact that the coupling constant \(\Theta_3\) multiplies a total derivative. In QCD, however, the term still has physical significance. Moreover, the term actually violates charge-parity (CP) symmetry.

The fact that no such effects are observed implies that \(\Theta_3\) is either 0 or at least, very small. Now why would \(\Theta_3\) be very small? There is no natural explanation.

However, one can consider introducing a new scalar field into the theory, with specific properties. In particular this scalar field, which is called the axion and usually denoted by \(a\), causes \(\Theta_3\) to be replaced with \(\Theta_{3,{\rm eff}}=\Theta_3 + \left<a\right>/f_a\), where \(f_a\) is some energy scale. If the scalar field were massless, the theory would demand \(\left<a\right>/f_a\) to be exactly \(-\Theta_3\). However, if the scalar field is massive, a small residual value for \(\Theta_{3,{\rm eff}}\) remains.

As for the Josephson-junction, it is a superconducting device in which two superconducting layers are separated by an isolation layer (which can be a normal conductor, a semiconductor, or even an insulator). As a voltage is introduced across a Josephson-junction, a current can be measured. The peculiar property of a Josephson-junction is the current does not vanish even as the voltage is reduced to zero:

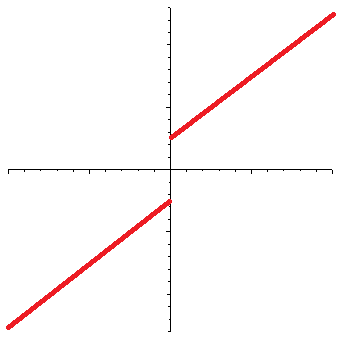
(The horizontal axis is voltage, the vertical axis is the current. In a normal resistor, the current-voltage curve would be a straight line that goes through the origin.) This is the DC Josephson effect; a similar effect arises when an AC voltage is applied, but in that case, the curve is even more interesting, with a step function appearance.

The phase difference \(\delta\) between the superconductors a Josephson-junction is characterized by the equation

\begin{align}\ddot{\delta}+\frac{1}{RC}\dot{\delta}+\frac{2eI_c}{\hbar C}\sin\delta&=\frac{2e}{\hbar C}I,\end{align}

where \(R\) and \(C\) are the resistance and capacitance of the junction, \(I_c\) is the critical current that characterizes the junction, and \(I\) is the current. (Here, \(e\) is the electron’s charge and \(\hbar\) is the reduced Planck constant.)

Given an axion field, represented by \(\theta=a/f_a\), in the presence of strong electric (\({\bf E}\)) and magnetic (\({\bf B}\)) fields, the axion field satisfies the equation

\begin{align}\ddot{\theta}+\Gamma\dot{\theta}+\frac{m_a^2c^4}{\hbar^2}\sin\theta=-\frac{g_\lambda c^3e^2}{4\pi^2f_a^2}{\bf E}{\bf B},\end{align}

where \(\Gamma\) is a damping parameter and \(g_\lambda\) is a coupling constant, while \(m_a\) is the axion mass and of course \(c\) is the speed of light.

The formal similarity between these two equations is striking. Now Beck suggests that the similarity is more than formal: that in fact, under the right circumstances, the axion field and a Josephson-junction can form a coupled system, in which resonance effects might be observed. The reason Beck gives is that the axion field causes a small CP symmetry perturbation in the Josephson-junction, to which the junction reacts with a small response in \(\delta\).

Indeed, Beck claims that this effect was, in fact, observed already, in a 2004 experiment by Hoffman, et al., who attempted to measure the noise in a certain type of Josephson-junction. In their experiment, a small, persistent peak appeared at a voltage of approximately 0.055 mV:

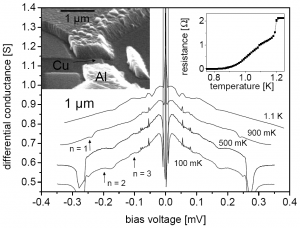
If Beck is correct, this observation corresponds to an axion with a mass of 0.11 meV (that is to say, the electron is some five billion times heavier than this axion) and the local density of the axion field would be about one sixth the presumed dark matter density in this region of the Galaxy.

I don’t know if Beck is right or not, but unlike most other papers about purported dark matter discoveries, this one does not feel like clutching at straws. It passes the “smell test”. I’d be very disappointed if it proved to be true (I am not very much in favor of the dark matter proposal) but if it is true, I think it qualifies as a Nobel-worthy discovery. It is also eerily similar to the original discovery of the cosmic microwave background: it was first observed by physicists who were not at all interested in cosmology but instead, were just trying to build a low-noise microwave antenna.

While responding to a question on ResearchGate, I thought about black holes and event horizons.

When you study general relativity, you learn that a star that is dense enough and massive enough will undergo gravitational collapse. The result will be a black hole, an object from which nothing, not even light, can escape. A black hole is surrounded by a spherical surface, its event horizon. It is not a physical surface, but a region that is characterized by the fact that the geometric distortions of spacetime due to gravity become extreme here. Once you cross the horizon, there is no turning back. It acts as a one-way membrane. Anything inside will unavoidably fall into the so-called singularity at the center of the black hole. What actually happens there, no-one really knows; gravity becomes so strong that quantum effects cannot be ignored, but since we don’t have a working quantum theory of gravity, we can’t really tell what happens.

That said, when you study general relativity, you also learn that a distant observer (such as you) can never see the horizon form. The horizon will forever remain in the distant observer’s infinite future. Similarly, we never see an object (or even a ray of light) cross the horizon. For a distant observer, any information coming from that infalling object (or ray of light) will become dramatically redshifted, so much so that the object will appear to crawl to a halt, essentially remaining frozen near the horizon. But you won’t actually get a chance to see even that; that’s because due to the redshift, rays of light from the object will become ever longer wavelength radio waves, until they become unobservable. So why do we bother even thinking about something that provably never happens in a finite amount of time?

For one thing, we know that even though a distant observer cannot see a horizon form, an infalling observer can. So purely as a speculative exercise, we would like to know what this infalling observer might experience.

And then there is the surface of last influence. We may not see an object cross the horizon, but there is a point in time beyond which we can no longer influence an infalling object. That is because any influence from us, even a beam of light, will not reach the object before the object crosses the horizon.

This is best illustrated in a so-called Penrose diagram (named after mathematician Roger Penrose, but also known as a conformal spacetime diagram.) In this diagram, spacetime is represented using only two dimensions on a sheet of paper; two spatial dimensions are suppressed. Furthermore, the remaining two dimensions are grossly distorted, so much so that even the “point at infinity” is drawn at a finite distance from the origin. However, the distortion is not random; it is done in such a way that light rays are always represented by 45° lines. (Such angle-preserving transformations are called “conformal”; hence the name.)

So here is the conformal spacetime diagram for a black hole, showing also an infalling object and a distant observer trying to communicate with this object:

Time, in this diagram, passes from bottom to top. The world line of an object is a (not necessary straight) line that also moves from bottom to top, and is never more then 45° away from the vertical (as that would represent faster-than-light motion).

In this diagram, a piece of infalling matter crosses the horizon. It is clear from the diagram that once that happens, there is nothing that can be done to avoid hitting the singularity near the top of the diagram. To escape, the object would need to move faster than light, in order to cross, from the inside to the outside, the 45° line representing the horizon.

An observer traveling along with the infalling object can bounce, e.g., radar waves off that object. However, that cannot go on forever. Once the observer’s world line crosses the line drawn to represent the surface of last influence, his radar waves will no longer reach the infalling object outside the horizon. Any echo from the object, therefore, will not be seen outside the horizon; it will remain within the horizon and eventually be swallowed by the singularity.

So does the existence of this surface of last influence mean that the event horizon exists for real, even though we cannot see it? This was an argument made in the famous textbook on relativity, Gravitation by Misner, Thorne and Wheeler. However, I tend to disagree. Sure, once you cross the surface of last influence, you can no longer influence an infalling object. Nonetheless, you still won’t see the object actually cross the horizon. Moreover, if the object happens to be, say, a very powerful rocket, its pilot may still change his mind and turn around, eventually re-emerging from the vicinity of the black hole. The surface of last influence remains purely hypothetical in this case; it is defined by the intersection of the infalling object and the event horizon, something that never actually happens.