The reason for my trip to China was to participate in the 3rd workshop on the TianQin mission.
TianQin is a proposed space-borne gravitational wave detector. It is described in our paper, which was recently accepted for publication in Classical and Quantum Gravity. The name, as typical for China, is poetic: it means a zither or harp in space or perhaps (sounds much nicer in English) a celestial harp. A harp that resonates in response to continuous gravitational waves that come from binary pulsars.
Gravitational waves are notoriously hard to detect because they are extremely weak. To date, we only have indirect confirmation of gravitational waves: closely orbiting binary pulsars are known to exhibit orbital decay that is consistent with the predictions of Einstein’s gravity.
Gravitational radiation is quadrupole radiation. It means basically that it simultaneously squeezes spacetime in one direction and stretches it in a perpendicular direction. This leads to the preferred method of detection: two perpendicular laser beams set to interfere with each other. As a gravitational wave passes through, a phase shift occurs as one beam travels a slightly longer, the other a slightly shorter distance. This phase shift manifests itself as an interference pattern, which can be detected.
But detection is much harder in practice than it sounds. Gravitational waves are not only very weak, they are also typically very low in frequency. Strong gravitational waves (relatively speaking) are produced by binaries such as HM Cancri (aka. RX J0806.3+1527) but even such an extreme binary system has an orbital period of several minutes. The corresponding gravitational wave frequency is measured in millihertz, and the wavelength, in tens or hundreds of millions of kilometers.
There is one exception: inspiraling neutron star or black hole binary systems at the very end of their lives. These could produce detectable gravitational waves with frequencies up to even a kilohertz or so, but these are random, transient events. Nonetheless, there are terrestrial detectors such as LIGO (Laser Interferometer Gravitational-wave Observatory) that are designed to detect such events, and the rumor I heard is that it may have already happened. Or not… let’s wait for the announcement.
But the continuous waves from close binaries require a detector comparable in size to the wavelength of their gravitational radiation. In short, an interferometer in which the laser beams can travel at least a few hundred thousand kilometers, preferably more. Which means that the interferometer must be in space.
This is the idea behind LISA, the Laser Interferometer Space Antenna project. Its current incarnation is eLISA (the “e” stands for “evolved”), a proposed European Space Agency mission, a precursor of which, LISA Pathfinder, was launched just a few days ago. Nonetheless, eLISA’s future remains uncertain.
Enter the Chinese, with TianQin. Whereas eLISA’s configuration of three spacecraft is designed to be in deep space orbiting one of the Earth-Sun Lagrange points with inteferometer arm lengths as long as 1.5 million kilometers, TianQin’s more modest proposal calls for a geocentric configuration, with arm lengths of 150,000 km or so. This means reduced sensitivity, of course, and the geocentric orbit introduces unique challenges. Nonetheless, our colleagues believe that it is fundamentally feasible for TianQin to detect gravitational waves from a known source with sufficient certainty. In other words, the primary mission objective of TianQin is to serve as a gravitational wave detector, confirming the existence of continuous waves emitted by a known binary system, as opposed to being an observatory, usable to find previously unknown sources of gravitational radiation. Detection is always easier: in radio technology, for instance, a lock-in amplifier can be used to detect the presence of a carrier wave even when it is far too weak to carry any useful information.
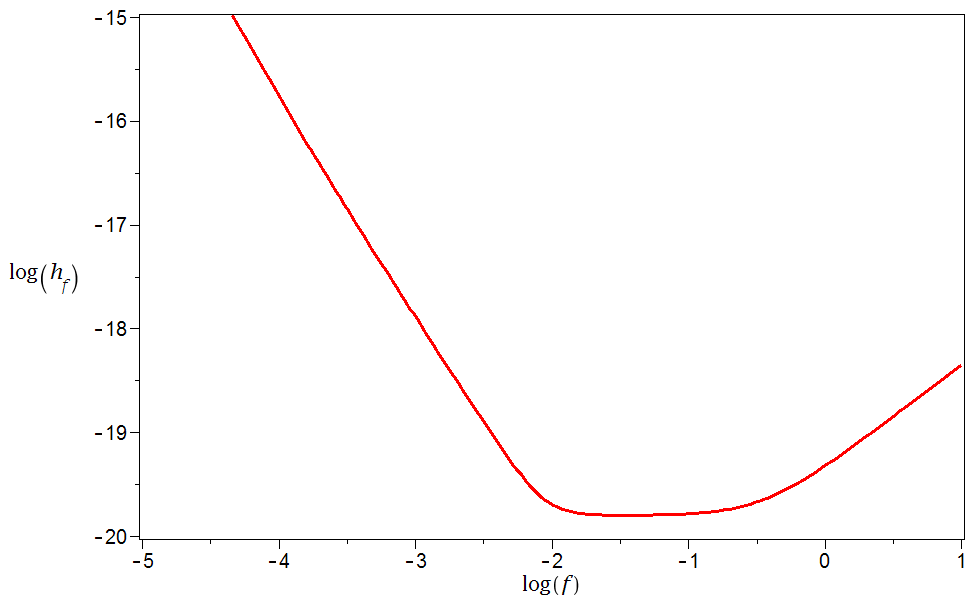 |
| Theoretical sensitivity curve of the proposed TianQin mission. |
The challenges of TianQin are numerous, but here are a few main ones:
- First, precisely controlling the orbits of shielded, drag-free test masses such that their acceleration due to nongravitational forces is less than \(10^{-15}~{\rm m}/{\rm s}^2\).
- Second, precisely controlling the optical path such that no unmodeled effects (e.g., thermal expansion due to solar heating) contribute unmodeled changes more than a picometer in length.
- Third, implementing time-delay interferometry (TDI), which is necessary in order to be able to compare the phases of laser signals that traveled different lengths, and do so with sufficient timing accuracy to minimize the contributions due to fluctuations in laser frequency.
Indeed, some of the accuracy requirements of TianQin exceed those of eLISA. This is a tall order for any space organization, and China is no exception. Still, as they say, where there is a will…
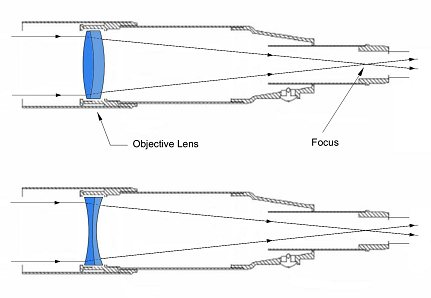
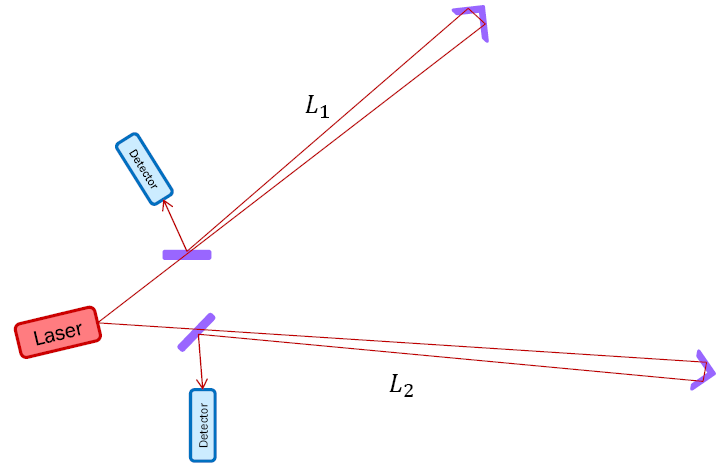 |
| Unequal-arm Michelson interferometer. |
One thing that complicates matters is that there are legal barriers when it comes to cooperation with China. In the United States there are strong legal restrictions preventing NASA and researchers at NASA from cooperating with Chinese citizens and Chinese enterprises. (Thankfully, Canada is a little more open-minded in this regard.) Then there is the export control regime: Technologies that can be utilized to navigate ballistic missiles, to offer satellite-based navigation on the ground, and to perform remote sensing may be categorized as munitions and fall under export control restrictions in North America, with China specifically listed as a proscribed country.
The know-how (and software) that would be used to navigate the TianQin constellation is arguably subject to such restrictions at least on the first two counts, but possibly even the third: a precision interferometer in orbit can be used for gravitiational remote sensing, as it has been amply demonstrated by GRACE (Gravity Recovery And Climate Experiment), which was orbiting the Earth, and GRAIL (Gravity Recovery And Interior Laboratory) in lunar orbit. Then there is the Chinese side of things: precision navigation requires detailed information about the capabilities of tracking stations in China, which may be, for all I know, state secrets.
While these issues make things a little tricky for Western researchers, TianQin nonetheless has a chance of becoming a milestone experiment. I sincerely hope that they succeed. And I certainly feel honored, having been invited to take part in this workshop.










 A physics meme is circulating on the Interwebs, suggesting that any length shorter than the so-called Planck length makes “no physical sense”.
A physics meme is circulating on the Interwebs, suggesting that any length shorter than the so-called Planck length makes “no physical sense”.