On my eighth birthday, I received a gift from a nice couple, friends of my Mom.
It was a Hungarian-language book bearing the title, “Wonders of the World,” in Hungarian, translated from the German original that was written by German-Jewish authors Artur Fürst and Alexander Moszkowski.
It was an old book, published in the 1930s. A dark green hardcover, with the etched image of a skyscraper for illustration on the cover. Its dust jacket, if it ever had one, was long gone.

But never mind that, it’s the content on these yellowed pages that matters.
It was from this book that I first learned about statistical fallacies, for instance. What is the probability that when you leave your home, the first 200 people you encounter are all males? Astronomically small, you might conclude. 2−200 ~ 6.223 × 10−61 to be a bit more precise, assuming half the population is male. A probability this small is firmly in the category of never happens. Until one morning, you step outside and the first thing you see is an all-male battalion of soldiers marching down the street…
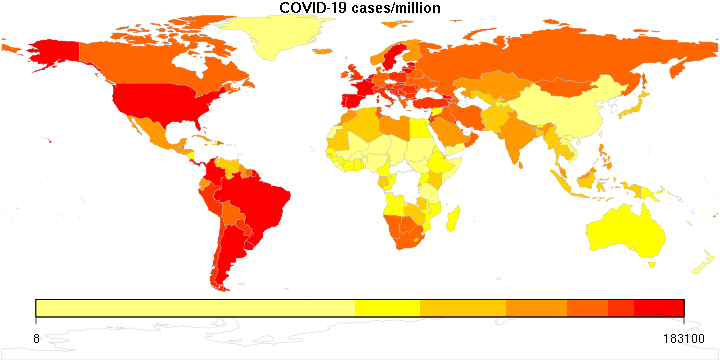
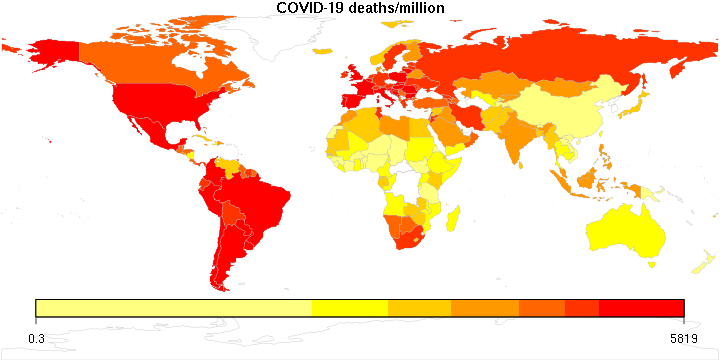
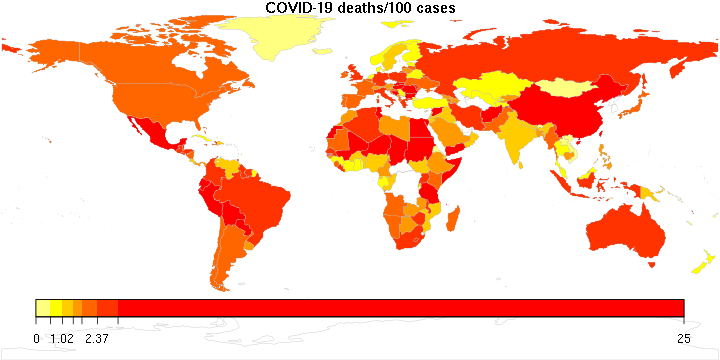
I was reminded of this book today as I was reading about recent pronouncements of “breakthrough” infections among the vaccinated, and the reminder by experts that in a population that has a high vaccination rate, such cases are to be expected. It does not mean that the vaccine is worthless. It simply means that as the virus runs out of unvaccinated victims, to the extent it can still cause damage, increasingly it will be among the vaccinated folks. Which should make sense, except, as we well know, roughly 90% of statistical fallacies are committed by right-handed people…
Anyhow, much to my surprise, this book I love so much, from which I learned so much as a pre-teen, remains well-known in the country where it was originally published under the title Das Buch der 1000 Wunder. So well-known, in fact, that current German-language editions are readily available on Amazon, nearly a century after its initial publication. So I guess I am not the only person who finds the insights and information presented in this unassuming volume immensely valuable, especially for a child.
So let this serve as my notice of gratitude across time and space to “uncle Sandor and aunt Eva,” as they inscribed their names in the book along with their birthday wishes, for what I can now truly call a gift of a lifetime.