So the big announcement was made yesterday: r = 0.2. The inflationary Big Bang scenario is seemingly confirmed.
If confirmed, this discovery is of enormous significance. (Of course, extraordinary claims require extraordinary evidence.)
So here is the thing. In gravity, just as in electromagnetism, outside of a spherically symmetric body, the field will be indistinguishable from that of a point source. So for instance, if the Earth were a perfect sphere, simply by looking at the orbit of the Moon, you could not possible tell if the Earth was tiny and superdense, or large and less dense… only that its total mass is roughly six quadrillion kilograms.
A consequence of this is that if a spherically symmetric body expands and contracts, its (electrical or gravitational) field does not change. In other words, there is no such thing as monopole radiation.
In the case of electromagnetism, we can separate positive and negative charges. Crudely speaking, this is what a transmitting antenna does… and as a result, it produces dipole radiation. However, there is no such thing as negative mass: hence, there is no such thing is dipole gravitational radiation.
The next thing happens when you take a spherically symmetric body and squeeze it in one direction while allowing it to expand in the other. When you do this, the (electric or gravitational) field of the body will change. These changes will propagate in the form of quadrupole radiation. This is the simplest form of gravitational waves that there is. This method of generating radiation is very inefficient… which is one of the reasons why gravitational waves are both hard to produce and hard to detect.
To date, nobody detected gravitational waves directly. However, we did detect changes in the orbital periods of binary pulsars (superdense stars orbiting each other in very tight orbits) that is consistent with the loss of kinetic energy due to gravitational radiation.
Gravitational radiation was also produced when the Universe was very young, very dense, expanding rapidly. One particular theory of the early expansion is the inflationary theory, which suggests that very early, for a short time the Universe underwent extremely rapid expansion. This may explain things such as why the observable Universe is as homogeneous, as “flat” as it appears to be. This extremely rapid expansion would have produced strong gravitational waves.
Our best picture of the early Universe comes from our observations of the cosmic microwave background: leftover light from when the Universe was about 380,000 years old. This light, which we see in the form of microwave radiation, is extremely smooth, extremely uniform. Nonetheless, its tiny bumps already tell us a great deal about the early Universe, most notably how structures that later became planets and stars and galaxies began to form.
This microwave radiation, like all forms of electromagnetic radiation including light, can be polarized. Normally, you would expect the polarization to be random, a picture kind of like this one:
However, the early Universe already had areas that were slightly denser than the rest (these areas were the nuclei around which galaxies later formed.) Near such a region, the polarization is expected to line up preferably in the direction of the excess density, perhaps a little like this picture:
This is called the scalar mode or E-mode.
Gravitational waves can also cause the polarization of microwaves to line up, but somewhat differently, introducing a twist if you wish. This so-called tensor mode or B-mode pattern will look more like this:
We naturally expect to see B-modes as a result of the early expansion. We expect to see an excess of B-modes if the early expansion was governed by inflation.
And this is exactly what the BICEP2 experiment claims to have found. The excess is characterized by the tensor-to-scalar ratio, r = 0.2, and they claim it is a strong, five-sigma result.
Two questions were raised immediately concerning the validity of this result. First, why was this not detected earlier by the Planck satellite? Well, according to the paper and the associated FAQ, Planck only observed B-modes indirectly (inferred from temperature fluctuation measurements) and in any case, the tension between the two results is not that significant:
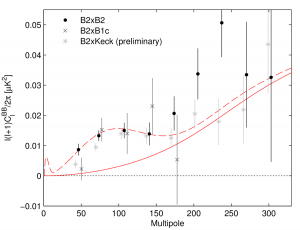
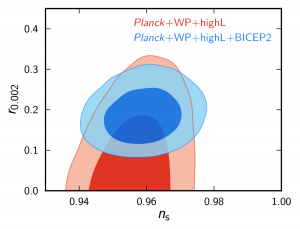 The other concern is that they seem to show an excess at higher multipole moments. This may be noise, a statistical fluke, or an indication of an unmodeled systematic that, if present, may degrade or even wipe out the claimed five sigma result:
The other concern is that they seem to show an excess at higher multipole moments. This may be noise, a statistical fluke, or an indication of an unmodeled systematic that, if present, may degrade or even wipe out the claimed five sigma result:
The team obviously believes that their result is robust and will withstand scrutiny. Indeed, they were so happy with the result that they decided to pay a visit to Andrei Linde, one of the founding fathers, if you wish, of inflationary cosmology:
What can I say? I hope there will be no reason for Linde’s genuine joy to turn into disappointment.
As to the result itself… apparent confirmation of a prediction of the inflationary scenario means that physical cosmology has reached the point where it can make testable predictions about the Universe when its age, as measured from the Big Bang, was less than one one hundredth of a quintillionth of a second. That is just mind-bogglingly insane.
 Richard Feynman’s Lectures on Physics remains a classic to this day.
Richard Feynman’s Lectures on Physics remains a classic to this day.

 A physics meme is circulating on the Interwebs, suggesting that any length shorter than the so-called Planck length makes “no physical sense”.
A physics meme is circulating on the Interwebs, suggesting that any length shorter than the so-called Planck length makes “no physical sense”.









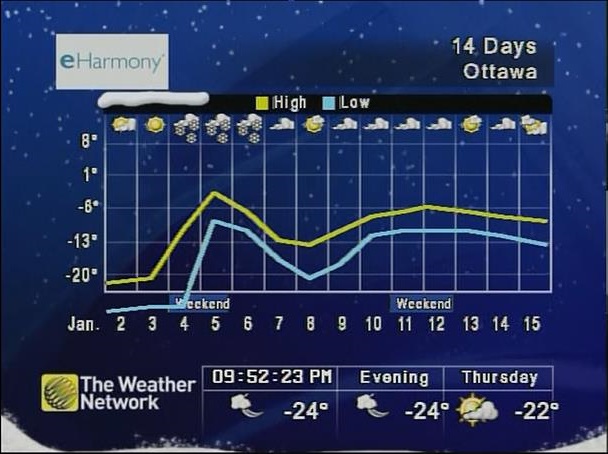

 Damn it’s cold this morning. Negative 26 Centigrade. Or 27 if I believe the local news. And it’s not even winter yet!
Damn it’s cold this morning. Negative 26 Centigrade. Or 27 if I believe the local news. And it’s not even winter yet!