So the other day, I solved this curious mathematics puzzle using repeated applications of Pythagoras’s theorem and a little bit of algebra.
Now I realize that there is a much simpler form of the proof.
The exercise was to prove that, given two semicircles drawn into a bigger circle as shown below, the sum of the areas of the semicircles is exactly half that of the larger circle.
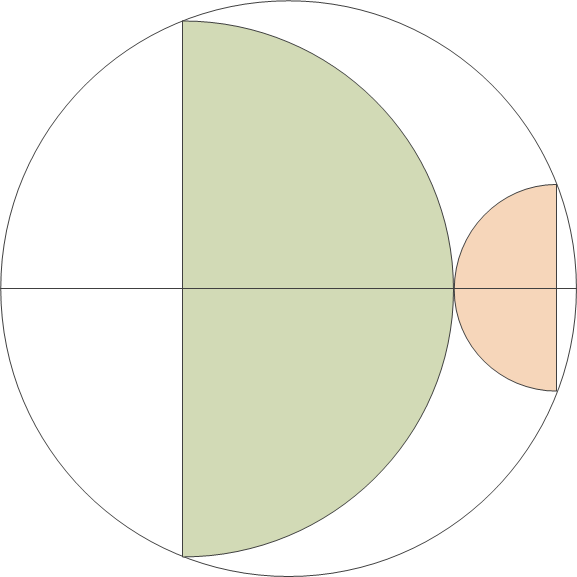
Again, I’m inserting a few blank lines before presenting my proof.
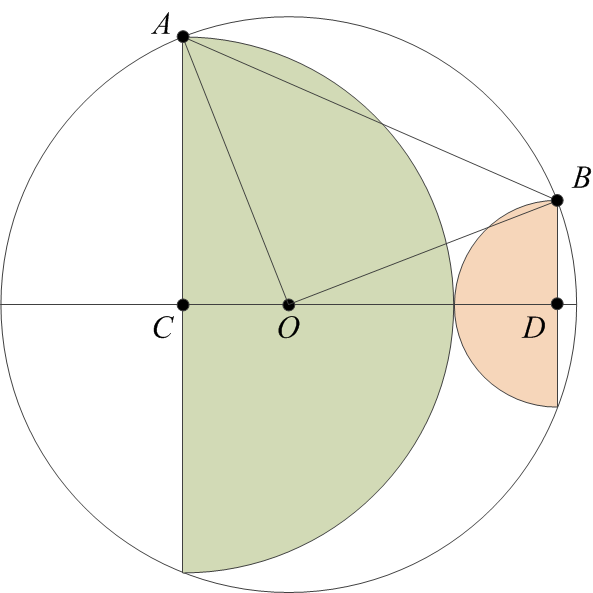
Once again I am labeling some vertices in the diagram for easy reference.
Our goal is to prove that the area of a circle with radius AO is twice the sum of the areas of two semicircles, with radii AC and BD. But that is the same as proving that the area of a circle with radius AO is equal to the sum of the areas of two circles, with radii AC and BD.
The ACO< angle is a right angle. Therefore, the area of a circle with radius AO is the sum of the areas of circles with radii AC and CO. (To see this, just multiply the theorem of Pythagoras by π.) So if only we could prove that CO = BD, our proof would be complete.
Since AO = BO, they are the sides of the isosceles triangle ABO. Now if we were to pick a point O‘ on the line CD such that CO‘ = BD, the ACO‘ and O‘DB triangles will be identical (CD being the sum of AC and BD by construction). Therefore, AO‘ = BO‘, and the ABO‘ triangle would be another isosceles triangle with its third vertex on the CD line. Clearly that is not possible, so O = O‘, and therefore, CO = BD. This concludes the proof.