The other day, I ran across a cute geometry puzzle on John Baez’s Google+ page. I was able to solve it in a few minutes, before I read the full post that suggested that this was, after all, a harder-than-usual area puzzle. Glad to see that, even though the last high school mathematics competition in which I participated was something like 35 years ago, I have not yet lost the skill.
Anyhow, the puzzle is this: prove that the area of the two semicircles below is exactly half the area of the full circle.
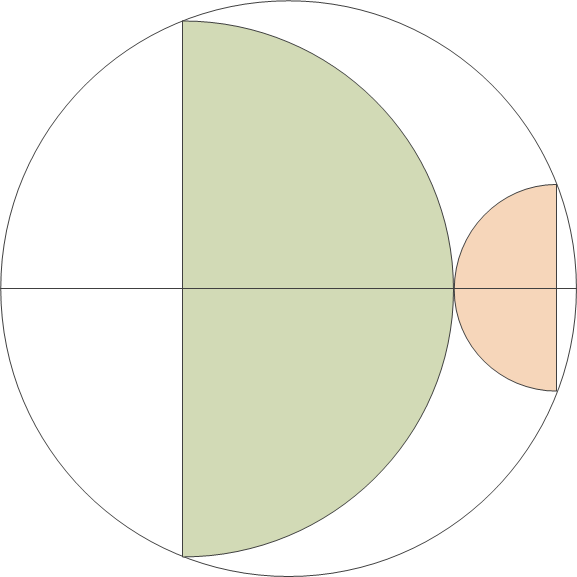
I am going to insert a few blank lines here before providing my solution.
I start with labeling some vertices on the diagram and also drawing a few radii and other lines to help.
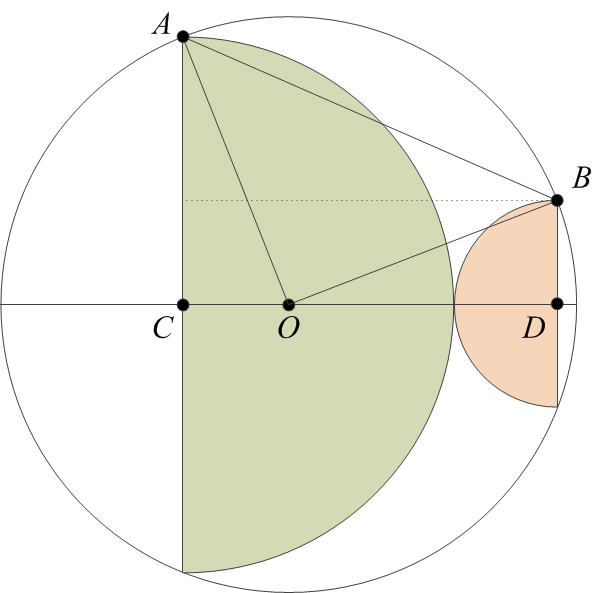
Next, let’s call the radii of the two semicircles as \(a\) and \(b\). Then, we have
\begin{align}
(AC)&= a,\\
(BD)&= b.
\end{align}Now observe that
\begin{align}
(OA) = (OB) = r,
\end{align}and also
\begin{align}
(CD)&= a + b,\\
(OD)&= a + b~- (OC).
\end{align}The rest is just repeated application of the theorem of Pythagoras:
\begin{align}
(OC)^2&= r^2 – a^2,\\
(OD)^2&= r^2 – b^2,
\end{align}followed by a bit of trivial algebra:
\begin{align}
(OC)^2 + a^2&= [a + b – (OC)]^2 + b^2,\\
0&= 2(a + b)[b – (OC)],\\
(OC)&= b.
\end{align}Therefore,
\begin{align}
a^2+b^2=r^2,
\end{align}which means that the area of the full circle is twice the sum of the areas of the two semicircles, which is what we set out to prove.
I guess I have not yet lost my passion for pointless, self-serving mathematics.