Slava Turyshev and I just published a paper in Physical Review. It is a lengthy, quite technical paper about the wave-theoretical treatment of the solar gravitational telescope.
What, you say?
Well, simple: using the Sun as a gravitational telescope to image distant objects. Like other stars, the Sun bends light, too. Measuring this bending of light was, in fact, the crucial test carried out by Eddington during the 1919 solar eclipse, validating the predictions of general relativity and elevating Albert Einstein to the status of international science superstar.
The gravitational bending of light is very weak. Two rays, passing on opposite sides of the Sun, are bent very little. So little in fact, it takes some 550 astronomical units (AU; the distance between the Earth and the Sun) for the two rays to meet. But where they do, interesting things happen.
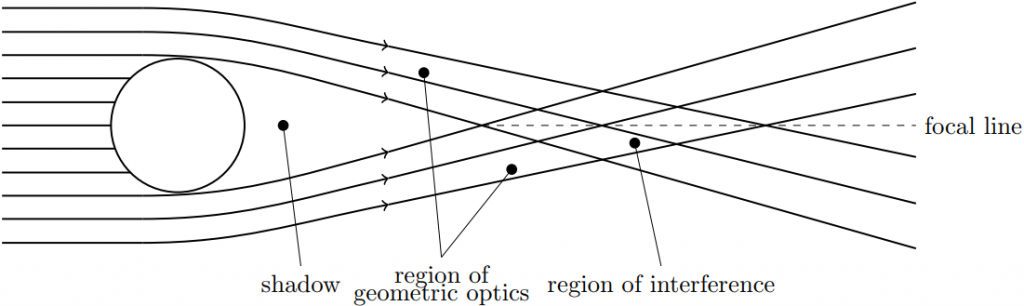
If you were floating in space at that distance, and there was a distant planet on the exact opposite side of the Sun, light from a relatively small section of that planet would form a so-called Einstein ring around the Sun. The light amplification would be tremendous; a factor of tens of billions, if not more.
But you have to be located very precisely at the right spot to image a particular spot on the exoplanet. How precisely? Well, that’s what we set out to figure out, based in part on the existing literature on the subject. (Short answer: it’s measured in tens of centimeters or less.)
In principle, a spacecraft at this distance, moving slowly in lateral directions to scan the image plane (which is several kilometers across), can obtain a detailed map of a distant planet. It is possible, in principle, to obtain a megapixel resolution image of a planet dozens of light years from here, though image reconstruction would be a task of considerable complexity, due in part to the fact that an exoplanet is a moving, changing target with variable illumination and possibly cloud cover.
Mind you, getting to 550 AU is costly. Our most distant spacecraft to date, Voyager 1, is just under 140 AU from the Sun, and it took that spacecraft 40 years to get there. That said, it is a feasible mission concept, but we must be very certain that we understand the physics thoroughly.
This is where our paper comes in: an attempt to derive detailed results about how light waves pass on both sides of the Sun and recombine along the focal line.
The bulk of the work in this paper is Slava’s, but I was proud to help. Part of my contribution was to provide a visualization of the qualitative behavior of the wavefront (described by a hypergeometric function):

In this image, a light wave, initially a plane wave, travels from left to right and it is deflected by a gravitational source at the center. If you squint just a little, you can actually see a concentric circular pattern overlaid on top of the distorted wavefront. The deflection of the wavefront and this spherical wave perturbation are both well described by an approximation. However, that approximation breaks down specifically in the region of interest, namely the focal line:

The top left of these plots show the approximation of the deflected wavefront; the top right, the (near) circular perturbation. Notice how both appear to diverge along the focal line: the half line between the center of the image and the right-hand side. The bottom right plot shows the combination of the two approximations; it is similar to the full solution, but not identical. The difference between the full solution and this approximation is shown in the bottom left plot.
I also helped with working out evil-looking things like a series approximation of the confluent hypergeometric function using so-called Pochhammer symbols and Stirling numbers. It was fun!
To make a long story short, although it involved some frustratingly long hours at a time when I was already incredibly busy, it was fun, educational, and rewarding, as we gave birth to a 39-page monster (43 pages on the arXiv) with over 300 equations. Hopefully just one of many contributions that, eventually (dare I hope that it will happen within my lifetime?) may result in a mission that will provide us with a detailed image of a distant, life-bearing cousin of the Earth.