We have a new manuscript on arXiv. Its title might raise some eyebrows: Algebraic wave-optical description of a quadrupole gravitational lens.
Say what? Algebra? Wave optics? Yes. It means that in this particular case, namely a gravitational lens that is described as a gravitational monopole with a quadrupole correction, we were able to find a closed form description that does not rely on numerical integration, especially no numerical integration of a rapidly oscillating function.
Key to this solution is a quartic equation. Quartic equations were first solved algebraically back in the 16th century by Italian mathematicians. The formal solution is usually considered to be of little practical value, as it entails cumbersome algebra, and polynomial equations can be routinely and efficiently solved using numerical methods.
But in this case… The amazing thing is that the algebraic solution reveals so much about the physics itself!
Take this figure from our paper, for instance:
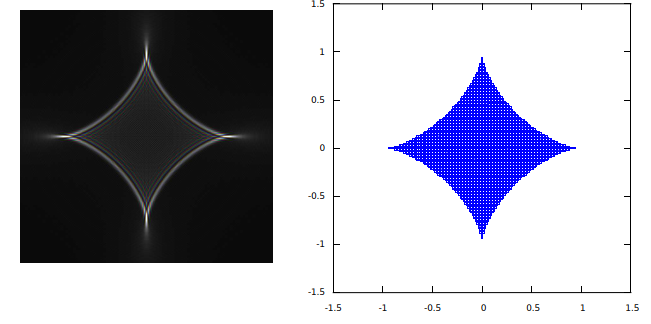
On the left is light projected by the gravitational lens, its so-called point-spread function (PSF) which tells us how light from a point source is distributed on an imaginary projection screen by the lens. On the right? Why, that’s the discriminant of the quartic equation
$$ x^4-2\eta\sin\mu \, x^3+\big(\eta^2-1\big)x^2+\eta\sin\mu \, x+{\textstyle\frac{1}{4}}\sin^2\mu=0, $$
in a plane characterized by polar coordinates \((\eta,\tfrac{1}{2}\mu)\), that is, \(\eta\) as a radial coordinate and \(\tfrac{1}{2}\mu \) as an azimuthal angle. When the discriminant is positive, the equation is expected to have four real (or four complex) roots; everywhere else, it’s a mix of real and imaginary roots. This direct connection between the algebra and the lensing phenomenon is unexpected and beautiful.
The full set of real roots of this equation can be shown in the form of an animation:
Of course one must read the paper in order for this animation to make sense, but I think it’s beautiful.
How good is this quartic solution? It is uncannily accurate. Here is a comparison of the PSF computed using the quartic solution and also using numerical integration, as well as some enlarged details from the so-called caustic boundary:
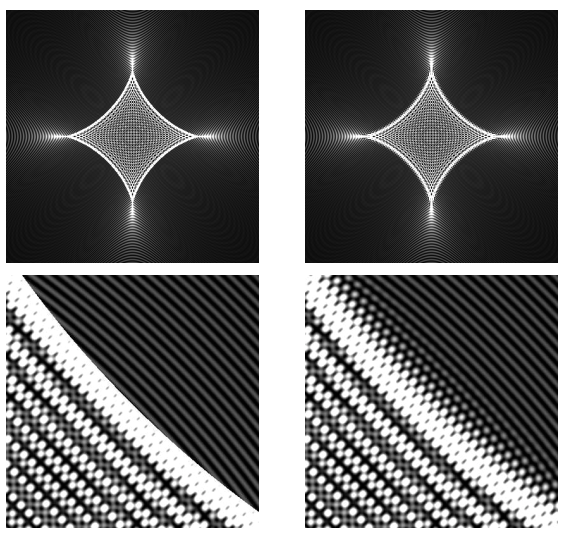
It’s only in the immediate vicinity of the caustic boundary that the quartic solution becomes less than accurate.
We can also use the quartic solution to simulate images seen through a telescope (i.e., the Einstein ring, or what survives of it, that would appear around a gravitational lens when we looked at the lens through a telescope with a point source of light situated behind the lens.) We can see again that it’s only in the vicinity of the caustic boundary that the quartic solution produces artifacts instead of accurately reproducing it when spots of light widen into arcs:
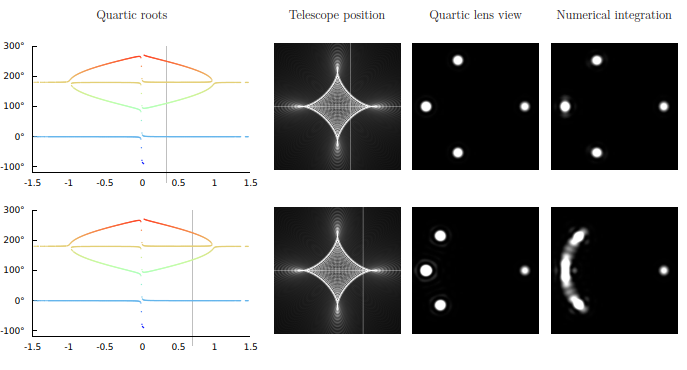
This paper was so much joy to write! Also, for the first time in my life, this paper gave us a legitimate, non-pretentious reason to cite something from the 16th century: Cardano’s 1545 treatise in which the quartic solution (as well as the cubic) are introduced, together with discussion on the meaning of taking the square root of negative numbers.