Now it is time for me to be bold and contrarian. And for a change, write about physics in my blog.
From time to time, even noted physicists express their opinion in public that we do not understand quantum physics. In the professional literature, they write about the “measurement problem”; in public, they continue to muse about the meaning of measurement, whether or not consciousness is involved, and the rest of this debate that continues unabated for more than a century already.
Whether it is my arrogance or ignorance, however, when I read such stuff, I beg to differ. I feel like the alien Narim in the television series Stargate SG-1 in a conversation with Captain (and astrophysicist) Samantha Carter about the name of a cat:
CARTER: Uh, see, there was an Earth physicist by the name of Erwin Schrödinger. He had this theoretical experiment. Put a cat in a box, add a can of poison gas, activated by the decay of a radioactive atom, and close the box.
NARIM: Sounds like a cruel man.
CARTER: It was just a theory. He never really did it. He said that if he did do it at any one instant, the cat would be both dead and alive at the same time.
NARIM: Ah! Kulivrian physics. An atom state is indeterminate until measured by an outside observer.
CARTER: We call it quantum physics. You know the theory?
NARIM: Yeah, I’ve studied it… in among other misconceptions of elementary science.
CARTER: Misconception? You telling me that you guys have licked quantum physics?
What I mean is… Yes, in 2021, we “licked” quantum physics. Things that were mysterious in the middle of the 20th century aren’t (or at least, shouldn’t be) quite as mysterious in the third decade of the 21st century.
OK, let me explain by comparing two thought experiments: Schrödinger’s cat vs. the famous two-slit experiment.
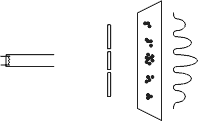
The two-slit experiment first. An electron is fired by a cathode. It encounters a screen with two slits. Past that screen, it hits a fluorescent screen where the location of its arrival is recorded. Even if we fire one electron at a time, the arrival locations, seemingly random, will form a wave-like interference pattern. The explanation offered by quantum physics is that en route, the electron had no classically determined position (no position eigenstate, as physicists would say). Its position was a combination, a so-called superposition of many possible position states, so it really did go through both slits at the same time. En route, its position operator interfered with itself, resulting in the pattern of probabilities that was then mapped by the recorded arrival locations on the fluorescent screen.
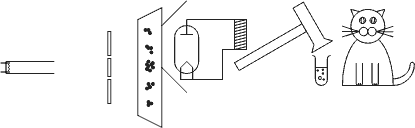
Now on to the cat: We place that poor feline into a box together with a radioactive atom and an apparatus that breaks a vial of poison gas if the atom undergoes fission. We wait until the half-life of that atom, making it a 50-50 chance that fission has occurred. At this point, the atom is in a superposition of intact vs. split, and therefore, the story goes, the cat will also be in a superposition of being dead and alive. Only by opening the box and looking inside do we “collapse the wavefunction”, determining the actual state of the cat.
Can you spot a crucial difference between these two experiments, though? Let me explain.
In the first experiment involving electrons, knowledge of the final position (where the electron arrives on the screen) does not allow us to reconstruct the classical path that the electron took. It had no classical path. It really was in a superposition of many possible locations while en route.
In the second experiment involving the cat, knowledge of its final state does permit us to reconstruct its prior state. If the cat is alive, we have no doubt that it was alive all along. If it is dead, an experienced veterinarian could determine the moment of death. (Or just leave a video camera and a clock in the box along with the cat.) The cat did have a classical state all throughout the experiment, we just didn’t know what it was until we opened the box and observed its state.
The crucial difference, then, is summed up thus: Ignorance of a classical state is not the same as the absence of a classical state. Whereas in the second experiment, we are simply ignorant of the cat’s state, in the first experiment, the electron has no classical state of position at all.
These two thought experiments, I think, tell us everything we need to know about this so-called “measurement problem”. No, it does not involve consciousness. No, it does not require any “act of observation”. And most importantly, it does not involve any collapse of the wavefunction when you really think it through. More about that later.
What we call measurement is simply interaction by the quantum system with a classical object. Of course we know that nothing really is classical. Fluorescent screens, video cameras, cats, humans are all made of a very large but finite number of quantum particles. But for all practical (measurable, observable) intents and purposes all these things are classical. That is to say, these things are (my expression) almost in an eigenstate almost all the time. Emphasis on “almost”: it is as near to certainty as you can possibly imagine, deviating from certainty only after the hundredth, the thousandth, the trillionth or whichever decimal digit.
Interacting with a classical object confines the quantum system to an eigenstate. Now this is where things really get tricky and old school at the same time. To explain, I must invoke a principle from classical, Lagrangian physics: the principle of least action. Almost all of physics (including classical mechanics, electrodynamics, even general relativity) can be derived from a so-called action principle, the idea that the system evolves from a known initial state to a known final state in a manner such that a number that characterizes the system (its “action”) is minimal.
The action principle sounds counterintuitive to many students of physics when they first encounter it, as it presupposes knowledge of the final state. But this really is simple math if you are familiar with second-order differential equations. A unique solution to such an equation can be specified in two ways. Either we specify the value of the unknown function at two different points, or we specify the value of the unknown function and its first derivative at one point. The former corresponds to Lagrangian physics; the latter, to Hamiltonian physics.
This works well in the context of classical physics. Even though we develop the equations of motion using Lagrangian physics, we do so only in principle. Then we switch over to Hamiltonian physics. Using observed values of the unknown function and its first derivative (think of these as positions and velocities) we solve the equations of motion, predicting the future state of the system.
This approach hits a snag when it comes to quantum physics: the nature of the unknown function is such that its value and its first derivative cannot both be determined as ordinary numbers at the same time. So while Lagrangian physics still works well in the quantum realm, Hamiltonian physics does not. But Lagrangian physics implies knowledge of the future, final state. This is what we mean when we pronounce that quantum physics is fundamentally nonlocal.
Oh, did I just say that Hamiltonian physics doesn’t work in the quantum realm? But then why is it that every quantum physics textbook begins, pretty much, with the Hamiltonian? Schrödinger’s famous equation, for starters, is just the quantum version of that Hamiltonian!
Aha! This is where the culprit is. With the Hamiltonian approach, we begin with presumed knowledge of initial positions and velocities (values and first derivatives of the unknown functions). Knowledge we do not have. So we evolve the system using incomplete knowledge. Then, when it comes to the measurement, we invoke our deus ex machina. Like a bad birthday party surprise, we open the magic box, pull out our “measurement apparatus” (which we pretended to not even know about up until this moment), confine the quantum system to a specific measurement value, retroactively rewrite the description of our system with the apparatus now present all along, and call this discontinuous change in the system’s description “wavefunction collapse”.
And then spend a century about its various interpretations instead of recognizing that the presumed collapse was never a physical process: rather, it amounts to us changing how we describe the system.
This is the nonsense for which I have no use, even if it makes me sound both arrogant and ignorant at the same time.
To offer a bit of a technical background to support the above (see my Web site for additional technical details): A quantum theory can be constructed starting with classical physics in a surprisingly straightforward manner. We start with the Hamiltonian (I know!), written in the following generic form:
$$H = \frac{p^2}{2m} + V({\bf q}),$$
where \({\bf p}\) are generalized momenta, \({\bf q}\) are generalized positions and \(m\) is mass.
We multiply this equation by the unit complex number \(\psi=e^{i({\bf p}\cdot{\bf q}-Ht)/\hbar}.\) We are allowed to do this trivial bit of algebra with impunity, as this factor is never zero.
Next, we notice the identities, \({\bf p}\psi=-i\hbar\nabla\psi,\) \(H\psi=i\hbar\partial_t\psi.\) Using these identities, we rewrite the equation as
$$i\hbar\partial_t\psi=\left[-\frac{\hbar^2}{2m}\nabla^2+V({\bf q})\right]\psi.$$
There you have it, the time-dependent Schrödinger equation in its full glory. Or… not quite, not yet. It is formally Schrödinger’s equation but the function \(\psi\) is not some unknown function; we constructed it from the positions and momenta. But here is the thing: If two functions, \(\psi_1\) and \(\psi_2,\) are solutions of this equation, then because the equation is linear and homogeneous in \(\psi,\) their linear combinations are also solutions. But these linear combinations make no sense in classical physics: they represent states of the system that are superpositions of classical states (i.e., the electron is now in two or more places at the same time.)
Quantum physics begins when we accept these superpositions as valid descriptions of a physical system (as indeed we must, because this is what experiment and observation dictates.)
The presence of a classical apparatus with which the system interacts at some future moment in time is not well captured by the Hamiltonian formalism. But the Lagrangian formalism makes it clear: it selects only those states of the system that are consistent with that interaction. This means indeed that a full quantum mechanical description of the system requires knowledge of the future. The apparent paradox is that this knowledge of the future does not causally influence the past, because the actual evolution of the system remains causal at all times: only the initial description of the system needs to be nonlocal in the same sense in which 19th century Lagrangian physics is nonlocal.