Message to Google: please do NOT start uploading photos from my phone to Google+ without first asking for my bleeping permission. I don’t care if only I see the pictures. I don’t want you to upload crap from my phone without asking, is that clear?
I may be a loyalist royalist but I don’t usually much care about the comings and goings of the Royal Family and I am no art critic either. However, I cannot refrain from commenting on the official portrait of Kate Middleton. It’s like all the goodness has been sucked out of her. Like a charmectomy operation. All the warmth that makes her photographs such a pleasure to look at… none if it is present in the painting. What was the artist thinking?
A few weeks ago, I exchanged a number of e-mails with someone about the Lanczos tensor and the Weyl-Lanczos equation. One of the things I derived is worth recording here for posterity.
The Lanczos tensor is an interesting animal. It can be thought of as the source of the Weyl curvature tensor, the traceless part of the Riemann curvature tensor. The Weyl tensor, together with the Ricci tensor, fully determine the Riemann tensor, i.e., the intrinsic curvature of a spacetime. Crudely put, whereas the Ricci tensor tells you how the volume of, say, a cloud of dust changes in response to gravity, the Weyl tensor tells you how that cloud of dust is distorted in response to the same gravitational field. (For instance, consider a cloud of dust in empty space falling towards the Earth. In empty space, the Ricci tensor is zero, so the volume of the cloud does not change. But its shape becomes distorted and elongated in response to tidal forces. This is described by the Weyl tensor.
Because the Ricci tensor is absent, the Weyl tensor fully describes gravitational fields in empty space. In a sense, the Weyl tensor is analogous to the electromagnetic field tensor that fully describes electromagnetic fields in empty space. The electromagnetic field tensor is sourced by the four-dimensional electromagnetic vector potential (meaning that the electromagnetic field tensor can be expressed using partial derivatives of the electromagnetic vector potential.) The Weyl tensor has a source in exactly the same sense, in the form of the Lanczos tensor.
The electromagnetic field does not uniquely determine the electromagnetic vector potential. This is basically how integrals vs. derivatives work. For instance, the derivative of the function \(y=x^2\) is given by \(y’=2x\). But the inverse operation is not unambiguous: \(\int 2x~ dx=x^2+C\) where \(C\) is an arbitrary integration constant. This is a recognition of the fact that the derivative of any function in the form \(y=x^2+C\) is \(y’=2x\) regardless of the value of \(C\); so knowing only the derivative \(y’\) does not fully determine the original function \(y\).
In the case of electromagnetism, this freedom to choose the electromagnetic vector potential is referred to as the gauge freedom. The same gauge freedom exists for the Lanczos tensor.
Solutions for the Lanczos tensor for the simplest case of the Schwarzschild metric are provided in Wikipedia. A common characteristic of these solutions is that they yield a quantity that “blows up” at the event horizon. This runs contrary to accepted wisdom, namely that the event horizon is not in any way special; a freely falling space traveler would never know that he is crossing it.
But as it turns out, thanks to the gauge freedom of the Lanczos tensor, it is easy to construct a solution (an infinite family of solutions, as a matter of fact) that do not behave like this at the horizon.
Well, it was a fun thing to compute anyway.
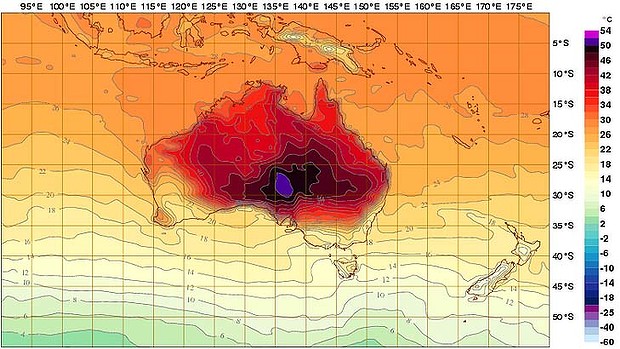
No, not Deep Purple the British hard rock group but deep purple the color. And pink… on Australian weather maps. These are the new colors to represent the temperature range between +50 and +54 degrees Centigrade.
There is another word to describe such temperatures: death. This is not funny anymore. If weather like this becomes more common, parts of our planet will simply become uninhabitable by humans without high technology life support (such as reliable, redundant air conditioning). In other words, it’s like visiting an alien planet.
Today’s Dilbert captured with remarkable acuity a situation that I (and probably, most other software developers) am all too familiar with:
I am supposed to be a geek but I guess I also have some chicken genes, since I never felt a particularly great urge to risk bricking my smartphone just for the sake of being able to run geeky apps on it that require root permission.
This all changed now that I actually have a spare smartphone, having accepted an early upgrade offer from Rogers. This spare, a SONY Xperia X10, served me faithfully for over two years. It is still a pretty decent phone, but I admit I like our new Samsung phones better.
So what does a cowardly geek do with a spare smartphone? Why, exactly what he did not dare to do while that smartphone was still in service. First, he tries to root it… which turned out to be a relatively easy process, although there were some tripping points like making sure that you enable USB debugging.
But while rooting the phone did let me do some fun things with it, the phone was still locked to the Rogers network. So I decided to take the plunge and purchase an unlock code for the grand total of about eight bucks from cellunlocker.net. (I picked this unlock provider after doing a bit of research; they seemed cheap yet reliable.) It took a bit longer than promised to get the unlock code (almost a full day instead of a few hours) but it worked as advertised.
So how do you test if the phone is unlocked? Well, it says that it is unlocked, but is it? My wife’s Samsung phone says it’s unlocked, too, but it rejects non-Rogers SIM cards. How do I know? I actually have two non-Rogers SIM cards, a non-registered one from a data stick I used to use in Hungary, and a registered and valid SIM card from my TELUS data stick. I shoved this one into the X10 and presto… it works! In fact, much to my surprise, it seems to work as a phone, too, although I am loathe to try to make calls with it, as I have no idea how much TELUS would charge for a voice call on what is supposedly a data only plan.
So what will I do the next time I travel overseas? Take this X10 with me to use with a local provider’s SIM? Or perhaps unlock my new Samsung phone? Sounds like a plan… maybe I’ll have the courage to do so this time. For what it’s worth, I did order a cheap micro-SIM cutter and a set of adapters that will help me cut down a regular SIM card to the size the Samsung phone accepts, yet still use that SIM card in other phones.
It will be fun.
Alas, the cat sanctuary on Parliament Hill is no more.
Now all we have there is politicians. This depresses me greatly.
Carr, Science 2013; 339:42-43
No, the title of this entry is not in reference to another miserably cold Ottawa winter (it’s not that cold, actually; I’ve seen a lot worse) but the absolute temperature scale.
Remember back in high school, when you were first taught that nothing can be colder than 0 degrees Kelvin? Well… you can’t say that anymore.
There are a variety of ways of formulating thermodynamics. Perhaps the cleanest is axiomatic thermodynamics, in which simple relationships like the conservation of energy or the existence of irreversible processes is codified in the form of axioms. One such axiom is often referred to as the Third Law of Thermodynamics; in essence, it postulates that a “ground state” of zero entropy exists, and associates this ground state with the start of the absolute temperature scale.
A little messier is classical statistical physics, where temperature is defined as the average kinetic energy per degree of freedom. Still, since kinetic energy cannot be negative, its average cannot be negative either, so it’s clear that there exists a lowest possible temperature at which all classical particles are at rest.
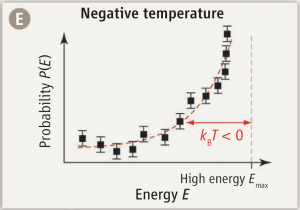
But statistical physics leads to another way of looking at temperature: as a means of calculating probabilities. The probability \(P_i\) of finding a particle in a state \(i\) with kinetic energy \(E_i\) will be proportional to the Boltzmann distribution:
$$P_i\propto e^{-E_i/kT},$$
where \(k\) is Boltzmann’s constant ant \(T\) is the temperature.
And here is where things get really interesting. For if it is possible to create an ensemble of particles in which \(P_i\) follows a positive exponential distribution, that clearly implies a negative temperature \(T\).
And this is precisely what has been reported in Science this week by Braun et al. (Science 2013; 339:52-55): an experimentally realized state of ultracold bosons with a distribution of kinetic (motional) energy states that follows a positive exponential curve. In other words… matter at temperature below 0 K.
How about that for a bit of 21st century physics.
This is what my cellphone greeted me with this morning:
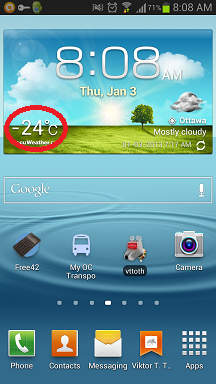
It wasn’t much warmer on our balcony either.
I was reading about Kim Jong Un’s unusual New Year’s message when I came across this video, a documentary by Dutch filmmaker Pieter Fleury, titled North Korea: A day in the life:
Even though it’s a few years old (it was made in 2004) and despite the fact that it was obviously made under the watchful eyes of North Korea’s censors, it still speaks volumes about the world’s last Stalinist state.