Carr, Science 2013; 339:42-43
No, the title of this entry is not in reference to another miserably cold Ottawa winter (it’s not that cold, actually; I’ve seen a lot worse) but the absolute temperature scale.
Remember back in high school, when you were first taught that nothing can be colder than 0 degrees Kelvin? Well… you can’t say that anymore.
There are a variety of ways of formulating thermodynamics. Perhaps the cleanest is axiomatic thermodynamics, in which simple relationships like the conservation of energy or the existence of irreversible processes is codified in the form of axioms. One such axiom is often referred to as the Third Law of Thermodynamics; in essence, it postulates that a “ground state” of zero entropy exists, and associates this ground state with the start of the absolute temperature scale.
A little messier is classical statistical physics, where temperature is defined as the average kinetic energy per degree of freedom. Still, since kinetic energy cannot be negative, its average cannot be negative either, so it’s clear that there exists a lowest possible temperature at which all classical particles are at rest.
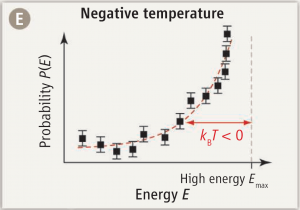
But statistical physics leads to another way of looking at temperature: as a means of calculating probabilities. The probability \(P_i\) of finding a particle in a state \(i\) with kinetic energy \(E_i\) will be proportional to the Boltzmann distribution:
$$P_i\propto e^{-E_i/kT},$$
where \(k\) is Boltzmann’s constant ant \(T\) is the temperature.
And here is where things get really interesting. For if it is possible to create an ensemble of particles in which \(P_i\) follows a positive exponential distribution, that clearly implies a negative temperature \(T\).
And this is precisely what has been reported in Science this week by Braun et al. (Science 2013; 339:52-55): an experimentally realized state of ultracold bosons with a distribution of kinetic (motional) energy states that follows a positive exponential curve. In other words… matter at temperature below 0 K.
How about that for a bit of 21st century physics.