No, the Earth’s core is not spinning backwards

 Geology, Physics  1 Response »
Jan 262023
 

“Stop the presses! The Earth’s core stopped spinning! In fact it is now spinning backwards!”

Well, that’s pretty much how much of the popular press handled a recent article, published in Nature Geoscience, under the far less pretentious title, “Multidecadal variation of the Earth’s inner-core rotation”.

And indeed, the first half-sentence in the abstract says it all (emphasis mine): “Differential rotation of Earth’s inner core relative to the mantle“.

It’s not like the core stopped spinning. It’s just that the core is sometimes spinning slightly faster, sometimes spinning slightly slower than the mantle, an oscillatory pattern that has to do with the complex interaction between the two.

How much faster/slower? Don’t expect anything dramatic. At most a few degrees a year, but more likely, just a small fraction of a degree a year. So even if the ~70-year cycle (deduced by the authors of the recent article — there are other estimates) is valid, the core would only get ahead, or behind, the mantle by just a few degrees before it slows down or catches up again.

And this is what supposedly happened: the core was slowing down until a few years ago, its rotation came to be in sync with that of the mantle. Slowing down further, it’s now falling ever so slightly behind, only to catch up again, presumably, a few decades from now.

The way it is misleadingly presented in the media and the degree to which it is sensationalized demonstrate that we live in the era of hype.

 Posted by at 6:21 pm

Fusion breakthrough?

 Physics  No Responses »
Dec 122022
 

The National Ignition Facility has achieved a net power gain in its experimental fusion reactor. This is heralded as a major breakthrough.

Does this mean that in 50 years, we will have practical nuclear fusion power our world?

Oh wait. We were told exactly that some 50 years ago:

At the beginning of the 1950s, it seemed that success is not far away. But later, difficulties arose one after another […]
…
Unfortunately today there are still gigantic difficulties in the path towards utilizing this fabulously rich supply of energy […]
…
In fourteen countries of the world, more than two thousand engineers and scientists are laboring on working out different types of fusion devices.
…
To date, more than a hundred different models have been devised […]
…
Let us introduce only one group of these: the Soviet Tokamak devices, because around the world, these are the ones in which researchers have the most faith, viewing them as prototypes of future fusion power plants.
…
A year and a half ago, in an experiment carried out in collaboration between Soviet and English physicists, they directly measured the temperature and density of the plasma of Tokamak-3, and it became clear that the results were even better than indicated by prior measurements. To date, no other device could produce plasma of such quality.
…
When will the first fusion power plants be realized, when will the investigation of controlled nuclear fusion exit the constraints of laboratory experiments? According to Professor Igor Golovin, the world-renowned expert on thermonuclear research, it will be possible to develop Tokamak devices into electricity-producing equipment by the last decade of our century. L. Hirsch, one of the leading physicists of the American Atomic Energy Commission is a little more cautious. According to him the path from the first experiments to the worldwide spread of fusion power plants is longer, and we’re lucky if they will enter the world’s energy production market in fifty years.

These are all quotes (my translations) from a 1972 Hungarian-language educational children’s publication, “Boys’ Almanac 1973”.

As I express my (probably uninformed) skepticism concerning practical fusion power generation, I note that in the deep interior of the Sun, under gravitational confinement due to the combined mass of more than 300,000 Earths, fusion progresses at the leisurely rate of a few hundred watts per cubic meter. (The power output of a well-maintained industrial compost pile.) For practical power generation, we need something that is at least a million times that, a few hundred megawatts per cubic meter… and we don’t have 300,000 Earths for gravitational confinement.

Of course I’d be delighted if they proved me wrong.

 Posted by at 1:09 pm

Priests and philosophers

 Personal, Physics  No Responses »
Nov 072022
 

Every so often, I am presented with questions about physics that go beyond physics: philosophical questions of an existential nature, such as the reasons why the universe has certain properties, or the meaning of existence in light of the far future.

I usually evade such questions by pointing out that they represent the domain of priests or philosophers, not physicists. I do not mean this disparagingly; rather, it is a recognition of the fact that physics is about how the universe works, not why, nor what it all means for us humans.

Yesterday, I came across a wonderful 1915 painting by Russian avant-garde painter Lyubov Popova, entitled Portrait of a Philosopher:

What can I say? This painting sums up how I feel perfectly.

 Posted by at 1:19 am

Bloggables

 Personal, Physics, Politics  No Responses »
Oct 242022
 

There are only about six days left of the month of October and I have not yet written anything in this blog of mine this month. I wonder why.

Ran out of topics? Not really, but…

… When it comes to politics, what can I say that hasn’t been said before? That the murderous mess in Ukraine remains as horrifying as ever, carrying with it the threat of escalation each and every day? That it may already be the opening battle of WW3?

Or should I lament how the new American radical right — masquerading as conservatives, but in reality anti-democratic, illiberal authoritarianists who are busy dismantling the core institutions of the American republic — is on the verge of gaining control of both houses of Congress?

Do I feel like commenting on what has been a foregone conclusion for months, Xi “Winnie-the-pooh” Jinping anointing himself dictator for life in the Middle Kingdom, ruining the chances of continuing liberalization in that great country, also gravely harming their flourishing economy?

Or should I comment on the fact that prevalent climate denialism notwithstanding, for the first time in the 35 years that I’ve lived in Ottawa, Canada, our air conditioner came online in the last week of October because the house was getting too hot in this near summerlike heat wave?

Naw. I should stick to physics. Trouble is, apart from the fact that I still feel quite unproductive, having battled a cold/flu/COVID (frankly, I don’t care what it was, I just want to recover fully) my physics time is still consumed with wrapping up a few lose ends of our Solar Gravitational Lens study, now that the NIAC Phase III effort has formally come to a close.

Still, there are a few physics topics that I am eager to revisit. And it’s a nice form of escapism from the “real” world, which is becoming more surreal each and every day.

 Posted by at 7:41 pm

Purple spiders in physics

 Physics  No Responses »
Sep 282022
 

I don’t always agree with Sabine Hossenfelder but every once in a while, she hits the nail spot on.

Case in point: Her article, published in The Guardian on September 26, about the state of particle physics.

Imagine going to a zoology conference, she says, where a researcher discusses a hypothesis (complete with a computer-generated 3D model) of a 12-legged purple spider living in the Arctic. Probably doesn’t exist but still, how about proposing a mission to the Arctic to search for one? After all, a null result also contains valuable data. Or how about a flying earthworm that lives in caves? Martian octopuses, anyone?

Zoology conferences do not usually discuss such imaginary monsters but, Sabine argues (and she is spot on) this is pretty much what particle physics conferences are like: “invent new particles for which there is no evidence, publish papers about them, write more papers about these particles’ properties, and demand the hypothesis be experimentally tested”. Worse yet, real money is being spent (wasted might be a better word) on carrying out such experiments.

She points out that while it is true that good science is falsifiable, the opposite isn’t always the case: Just because something is falsifiable does not make it good science.

And not just particle physics, I hasten to add. How about cosmology and gravitation? Discussions about what may or may not have happened during the Planck epoch? Exploring exotic spacetime topologies, often in dimensions other than four? And let me not even mention quantum computing or fusion energy…

Perhaps I am a born skeptic lacking imagination, but to me, these are all 12-legged purple Arctic spiders. The science we actually know and have the ability to confirm are general relativity in a spacetime that is by and large the perturbed Minkowski metric; and the Standard Model of particle physics, extended with a neutrino mass mixing matrix. These are the things that work. Not perfectly, mind you. General relativity needs “dark matter” (name aside, we don’t know what it is except that it has a dust equation of state) and “dark energy” (again, it has a name but beyond that, we don’t know what it is beyond its equation of state) to account for galaxy dynamics and cosmic evolution. The Hubble tension, the discrepancy between values of the Hubble parameter measured using different methods, is real. Observations by the James Webb space telescope suggest that we do not understand the “dark ages”, the first few hundred million years after the surface of last scattering (i.e., the epoch when the cosmic microwave background radiation was produced), well. Massive neutrinos invite the question about the apparent absence right-handed neutrinos.

And yes, we are very much in the blind concerning these issues. Nature has not yet provided hints and we are not smart enough to figure out the answers entirely on our own. But how is that an excuse for inventing 12-legged spiders?

I think it isn’t.

 Posted by at 6:40 pm

A silly idea that didn’t get me anywhere

 Physics  No Responses »
Sep 012022
 

A few days ago I had a silly thought about the metric tensor of general relativity.

This tensor is usually assumed to be symmetric, on account of the fact that even if it has an antisymmetric part, \(g_{[\mu\nu]}dx^\mu dx^\nu\) will be identically zero anyway.

But then, nothing constrains \(g_{\mu\nu}\) to be symmetric. Such a constraint should normally appear, in the Lagrangian formalism of the theory, as a Lagrange-multiplier. What if we add just such a Lagrange-multiplier to the Einstein-Hilbert Lagrangian of general relativity?

That is, let’s write the action of general relativity in the form,

$$S_{\rm G} = \int~d^4x\sqrt{-g}(R – 2\Lambda + \lambda^{[\mu\nu]}g_{\mu\nu}),$$

where we introduced the Lagrange-multiplier \(\lambda^{[\mu\nu]}\) in the form of a fully antisymmetric tensor. We know that

$$\lambda^{[\mu\nu]}g_{\mu\nu}=\lambda^{[\mu\nu]}(g_{(\mu\nu)}+g_{[\mu\nu]})=\lambda^{[\mu\nu]}g_{[\mu\nu]},$$

since the product of an antisymmetric and a symmetric tensor is identically zero. Therefore, variation with respect to \(\lambda^{[\mu\nu]}\) yields \(g_{[\mu\nu]}=0,\) which is what we want.

But what about variation with respect to \(g_{\mu\nu}?\) The Lagrange-multipliers represent new (non-dynamic) degrees of freedom. Indeed, in the corresponding Euler-Lagrange equation, we end up with new terms:

$$\frac{\partial}{\partial g_{\alpha\beta}}(\sqrt{-g}\lambda^{[\mu\nu]}g_{[\mu\nu]})=
\frac{1}{2}g^{\alpha\beta}\sqrt{-g}\lambda^{[\mu\nu]}g_{[\mu\nu]}+\sqrt{-g}\lambda^{[\mu\nu]}(\delta^\alpha_\mu\delta^\beta_\nu-\delta^\alpha_\nu\delta^\beta_\mu)=2\sqrt{-g}\lambda^{[\mu\nu]}=0.$$

But this just leads to the trivial equation, \(\lambda^{[\mu\nu]}=0,\) for the Lagrange-multipliers. In other words, we get back General Relativity, just the way we were supposed to.

So in the end, we gain nothing. My silly thought was just that, a silly exercise in pedantry that added nothing to the theory, just showed what we already knew, namely that the antisymmetric part of the metric tensor contributes nothing.

Now if we were to add a dynamical term involving the antisymmetric part, that would be different of course. Then we’d end up with either Einstein’s attempt at a unified field theory (with the antisymmetric part corresponding to electromagnetism) or Moffat’s nonsymmetric gravitational theory. But that’s a whole different game.

 Posted by at 11:40 pm

Differentiation

 Mathematics, Personal, Physics  No Responses »
May 252022
 

From time to time, I promise myself not to respond again to e-mails from strangers, asking me to comment on their research, view their paper, offer thoughts.

Yet from time to time, when the person seems respectable, the research genuine, I do respond. Most of the time, in vain.

Like the other day. Long story short, someone basically proved, as part of a lengthier derivation, that general relativity is always unimodular. This is of course manifestly untrue, but I was wondering where their seemingly reasonable derivation went awry.

Eventually I spotted it. Without getting bogged down in the details, what they did was essentially equivalent to proving that second derivatives do not exist:

$$\frac{d^2f}{dx^2} = \frac{d}{dx}\frac{df}{dx} = \frac{df}{dx}\frac{d}{df}\frac{df}{dx} = \frac{df}{dx}\frac{d}{dx}\frac{df}{df} = \frac{df}{dx}\frac{d1}{dx} = 0.$$

Of course second derivatives do exist, so you might wonder what’s happening here. The sleight of hand happens after the third equal sign: swapping differentiation with respect to two independent variables is permitted, but \(x\) and \(f\) are not independent and therefore, this step is illegal.

I pointed this out, and received a mildly abusive comment in response questioning the quality of my mathematics education. Oh well. Maybe I will learn some wisdom and refrain from responding to strangers in the future.

 Posted by at 11:46 pm

SciShow video on our Solar Gravitational Lens work

 Astronomy, Personal, Physics, Space  No Responses »
May 232022
 

This morning, Google greeted me with a link in its newsstream to a Hackaday article on the Solar Gravitational Lens. The link caught my attention right away, as I recognized some of my own simulated, SGL-projected images of an exo-Earth and its reconstruction.

Reading the article I realized that it appeared in response to a brand new video by SciShow, a science-oriented YouTube channel.

Yay! I like nicely done videos presenting our work and this one is fairly good. There are a few minor inaccuracies, but nothing big enough to be even worth mentioning. And it’s very well presented.

I suppose I should offer my thanks to SciShow for choosing to feature our research with such a well-produced effort.

 Posted by at 7:22 pm

No, a single Einstein ring snapshot won’t do the trick with the SGL

 Astronomy, Personal, Physics, Space  No Responses »
May 062022
 

A beautiful study was published the other day, and it received a lot of press coverage, so I get a lot of questions.

This study shows how, in principle, we could reconstruct the image of an exoplanet using the Solar Gravitational Lens (SGL) using just a single snapshot of the Einstein ring around the Sun.

The problem is, we cannot. As they say, the devil is in the details.

Here is a general statement about any conventional optical system that does not involve more exotic, nonlinear optics: whatever the system does, ultimately it maps light from picture elements, pixels, in the source plane, into pixels in the image plane.

Let me explain what this means in principle, through an extreme example. Suppose someone tells you that there is a distant planet in another galaxy, and you are allowed to ignore any contaminating sources of light. You are allowed to forget about the particle nature of light. You are allowed to forget the physical limitations of your cell phone’s camera, such as its CMOS sensor dynamic range or readout noise. You hold up your cell phone and take a snapshot. It doesn’t even matter if the camera is not well focused or if there is motion blur, so long as you have precise knowledge of how it is focused and how it moves. The map is still a linear map. So if your cellphone camera has 40 megapixels, a simple mathematical operation, inverting the so-called convolution matrix, lets you reconstruct the source in all its exquisite detail. All you need to know is a precise mathematical description, the so-called “point spread function” (PSF) of the camera (including any defocusing and motion blur). Beyond that, it just amounts to inverting a matrix, or equivalently, solving a linear system of equations. In other words, standard fare for anyone studying numerical computational methods, and easily solvable even at extreme high resolutions using appropriate computational resources. (A high-end GPU in your desktop computer is ideal for such calculations.)

Why can’t we do this in practice? Why do we worry about things like the diffraction limit of our camera or telescope?

The answer, ultimately, is noise. The random, unpredictable, or unmodelable element.

Noise comes from many sources. It can include so-called quantization noise because our camera sensor digitizes the light intensity using a finite number of bits. It can include systematic noises due to many reasons, such as differently calibrated sensor pixels or even approximations used in the mathematical description of the PSF. It can include unavoidable, random, “stochastic” noise that arises because light arrives as discrete packets of energy in the form of photons, not as a continuous wave.

When we invert the convolution matrix in the presence of all these noise sources, the noise gets amplified far more than the signal. In the end, the reconstructed, “deconvolved” image becomes useless unless we had an exceptionally high signal-to-noise ratio, or SNR, to begin with.

The authors of this beautiful study knew this. They even state it in their paper. They mention values such as 4,000, even 200,000 for the SNR.

And then there is reality. The Einstein ring does not appear in black, empty space. It appears on top of the bright solar corona. And even if we subtract the corona, we cannot eliminate the stochastic shot noise due to photons from the corona by any means other than collecting data for a longer time.

Let me show a plot from a paper that is work-in-progress, with the actual SNR that we can expect on pixels in a cross-sectional view of the Einstein ring that appears around the Sun:

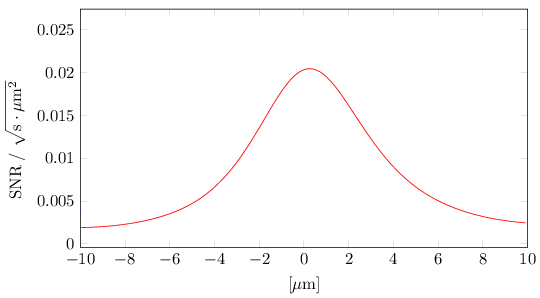
Just look at the vertical axis. See those values there? That’s our realistic SNR, when the Einstein ring is imaged through the solar corona, using a 1-meter telescope with a 10 meter focal distance, using an image sensor pixel size of a square micron. These choices are consistent with just a tad under 5000 pixels falling within the usable area of the Einstein ring, which can be used to reconstruct, in principle, a roughly 64 by 64 pixel image of the source. As this plot shows, a typical value for the SNR would be 0.01 using 1 second of light collecting time (integration time).

What does that mean? Well, for starters it means that to collect enough light to get an SNR of 4,000, assuming everything else is absolutely, flawlessly perfect, there is no motion blur, indeed no motion at all, no sources of contamination other than the solar corona, no quantization noise, no limitations on the sensor, achieving an SNR of 4,000 would require roughly 160 billion seconds of integration time. That is roughly 5,000 years.

And that is why we are not seriously contemplating image reconstruction from a single snapshot of the Einstein ring.

 Posted by at 4:01 pm

Maxima 5.46

 Computer Algebra, Personal, Physics  No Responses »
Apr 132022
 

Acting as “release manager” for Maxima, the open-source computer algebra system, I am happy to announce that just minutes ago, I released version 5.46.

I am an avid Maxima user myself; I’ve used Maxima’s tensor algebra packages, in particular, extensively in the context of general relativity and modified gravity. I believe Maxima’s tensor algebra capabilities remain top notch, perhaps even unsurpassed. (What other CAS can derive Einstein’s field equations from the Einstein-Hilbert Lagrangian?)

The Maxima system has more than half a century of history: its roots go back to the 1960s, when I was still in kindergarten. I have been contributing to the project for nearly 20 years myself.

Anyhow, Maxima 5.46, here we go! I hope I made no blunders while preparing this release, but if I did, I’m sure I’ll hear about it shortly.

 Posted by at 2:26 am

Satellite galaxies and tidal disruption

 Astronomy, Personal, Physics  No Responses »
Mar 242022
 

Between a war launched by a mad dictator, an occupation by “freedom convoy” mad truckers, and other mad shenanigans, it’s been a while since I last blogged about pure physics.

Especially about a topic close to my heart, modified gravity. John Moffat’s modified gravity theory MOG, in particular.

Back in 2020, a paper was published arguing that MOG may not be able to account for the dynamics certain galaxies. The author studied a large, low surface brightness galaxy, Antlia II, which has very little mass, and concluded that the only way to fit MOG to this galaxy’s dynamics is by assuming outlandish values not only for the MOG theory’s parameters but also the parameter that characterizes the mass distribution in the galaxy itself.

In fact, I would argue that any galaxy this light that does not follow Newtonian physics is bad news for modified theories of gravity; these theories predict deviations from Newtonian physics for large, heavy galaxies, but a galaxy this light is comparable in size to large globular clusters (which definitely behave the Newtonian way) so why would they be subject to different rules?

But then… For many years now, John and I (maybe I should only speak for myself in my blog, but I think John would concur) have been cautiously, tentatively raising the possibility that these faint satellite galaxies are really not very good test subjects at all. They do not look like relaxed, “virialized” mechanical systems; rather, they appear tidally disrupted by the host galaxy the vicinity of which they inhabit.

We have heard arguments that this cannot be the case, that these satellites show no signs of recent interaction. And in any case, it is never a good idea for a theorist to question the data. We are not entitled to “alternative facts”.

But then, here’s a paper from just a few months ago with a very respectable list of authors on its front page, presenting new observations of two faint galaxies, one being Antlia II: “Our main result is a clear detection of a velocity gradient in Ant2 that strongly suggests it has recently experienced substantial tidal disruption.”

I find this result very encouraging. It is consistent with the basic behavior of the MOG theory: Systems that are too light to show effects due to modified gravity exhibit strictly Newtonian behavior. This distinguishes MOG from the popular MOND paradigm, which needs the somewhat ad hoc “external field effect” to account for the dynamics of diffuse objects that show no presence of dark matter or modified gravity.

 Posted by at 2:30 am

Our galactic center

 Astronomy, Physics  No Responses »
Feb 192022
 

The 64-antenna radio telescope complex, MeerKAT, is South Africa’s contribution to the Square Kilometer Array, an international project under development to create an unprecedented radio astronomy facility.

While the SKA project is still in its infancy, MeerKAT is fully functional, and it just delivered the most detailed, most astonishing images yet of the central region of our own Milky Way. Here is, for instance, an image of the Sagittarius A region that also hosts the Milky Way’s supermassive black hole, Sgr A*:

The filamentary structure that is seen in this image is apparently poorly understood. As for the scale of this image, notice that it is marked in arc seconds; at the estimated distance to Sgr A, one arc second translates into roughly 1/8th of a light year, so the image presented here is roughly a 15 by 15 light year area.

 Posted by at 5:04 pm

In memoriam: Thanu Padmanabhan (1957-2021)

 Physics  No Responses »
Dec 202021
 

Though he passed away in September, I only learned about it tonight: Thanu Padmanabhan, renowned Indian theoretical physicist, is no longer with us. He was only 64 when he passed away, a result of a heart attack according to Wikipedia.

I never met Padmanabhan but I have several of his books on my bookshelf, including Structure Formation in the Universe and his more recent textbook Gravitation. I am also familiar with many of his papers.

I learned about his death just moments ago as I came across a paper by him on arXiv, carrying this comment: “Prof. T. Padmanabhan has passed away on 17th September, 2021, while this paper was under review in a journal.”

What an incredible loss. The brilliant flame of his intellect, extinguished. I am deeply saddened.

A tribute article about his life was published on arXiv back in October, but unfortunately was not cross-listed to gr-qc, and thus it escaped my attention until now.

 Posted by at 2:15 am

Rays of dark

 Personal, Physics  No Responses »
Oct 202021
 

Earlier today, I noticed something really strange. A lamp was radiating darkness. Or so it appeared.

Of course there was a mundane explanation. Now that the Sun is lower in the sky and the linden tree in front of our kitchen lost many of its leaves already, intense sunlight was reflecting off the hardwood floor in our dining area.

Still, it was an uncanny sight.

 Posted by at 11:27 pm

Why is my house… wobbly?

 Personal, Physics  2 Responses »
Sep 282021
 

I live in a condominium townhouse. We’ve been living here for 25 years. We like the place.

Our unit, in particular, is the middle unit in a three-unit block. The construction is reasonably sound: proper foundations, cinderblock firewalls between the units, woodframe construction within, pretty run-of-the-mill by early 1980s North American standards. We have no major complaints.

Except that… for the past several years, every so often the house wobbled a bit. Almost imperceptibly, but still. At first, I thought it was a minor earthquake (not uncommon in this region because it is still subject to isostatic rebound from the last ice age; in fact we did live through a couple of notable earthquakes since we moved in here.) But no, it was no earthquake.

I thought perhaps it was related to the downtown light rail tunnel construction? But no, the LRT tunnels are quite some ways from here and in any case, that part of the construction has been finished long ago.

But then what the bleep is it? Could I be just imagining things?

Our phones have very sensitive acceleration sensors. Not for the first time, I managed to capture one of these events. A little earlier this afternoon, I heard the woodframe audibly creak as the house began to move again. I grabbed my phone and turned on a piece of software that samples the acceleration sensor at a reasonably high rate, about 200 times a second. Here is the result of the first few seconds of sampling:

The sinusoidal signal is unmistakably there, confirmed by a quick Fourier-analysis to be a signal just above 3 Hz in frequency:

Like Sheldon Cooper in The Big Bang Theory, I can claim that no, I am not crazy, and in this case not because my mother had me tested but because my phone’s acceleration sensor confirms my perception: Something indeed wobbles the house a little, enough to register on my phone’s acceleration sensor, measuring a peak-to-peak amplitude of roughly 0.05 m/s² (the vertical axis in the first graph is in g-units.) That wobble is certainly not enough to cause damage, but it is, I admit, a bit unnerving.

So what is going on here? A neighbor engaging in some, ahem, vigorous activity? Our current neighbors are somewhat noisier than prior residents, occasionally training their respective herds of pygmy elephants to run up and down the stairs (or whatever it is that they are doing). But no, the events are just too brief in duration and too regular. Underground work, perhaps a secret hideout for the staff of the nearby Chinese embassy? Speaking of which, I admit I even thought that this ~3 Hz signal might be related to the reported cases of illness by embassy staff at several embassies around the world, but I just don’t see the connection: even if those cases are real and have an underlying common cause (as opposed to just mere random coincidences) it’s hard to see how a 3 Hz vibration can have anything to do with them.

OK, so I have a pretty good idea of what this thing isn’t, but then, what the bleepety-bleep is it?

 Posted by at 3:50 pm

Guilty as charged

 Humor, Personal, Physics  No Responses »
Aug 142021
 

I am not happy admitting it, but it’s true: There have been a few occasions in my life when I reacted just like this XKCD cartoon character when I first encountered specific areas of research.

 Posted by at 11:48 am

Steven Weinberg

 Physics  No Responses »
Jul 242021
 

Can you guess the author with the most physics books on what I call my “primary” bookshelf, the shelf right over my desk where I keep the books that I use the most often?

It would be Steven Weinberg. His 1972 Gravitation and Cosmology remains one of the best books ever on relativity theory, working out details in ways no other book does. His 2010 Cosmology remains a reasonably up-to-date textbook on modern cosmology. And then there is of course the 3-volume Quantum Theory of Fields.

Alas, Weinberg is no longer with us. He passed away yesterday, July 23, at the age of 88.

He will be missed.

 Posted by at 6:27 pm
 Older Entries  Newer Entries