A few months ago, a paper came to my attention; one written by a Hungarian climate scientist who supposedly resigned from his NASA job because he felt he was being muted by the climate science establishment. The paper was eventually published in a rather obscure journal, the quarterly journal of the Hungarian Meteorological Service. This paper has since been touted by its proponents as proof that the established climate models are bogus and that global warming is a hoax; on the other hand, it has been maligned by its critics, who declared it as junk science.
One notable point in Miskolczi’s paper is an unorthodox use of the virial theorem, and the funny thing is, while what he is doing is rather problematic, his critics fare no better; I’ve not seen anyone offer a technically correct analysis as to when the virial theorem might be applicable to describe a planetary atmosphere. (As a matter of fact, it is, but that doesn’t necessarily vindicate Miskolczi’s analysis.)
Miskolczi’s key result is that the atmosphere is in equilibrium in the sense that the greenhouse effect is already maximal; and so long as an effectively infinite reservoir of a potent greenhouse gas (water vapor) is available, this balance cannot be destroyed by changing the amount of CO2 in the air. However, this result may very well be a consequence of some trivial algebra that follows from some of Miskolczi’s more debatable assumptions.
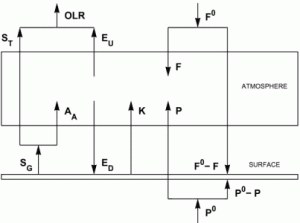
In his paper, Miskolczi presents a model of the atmosphere graphically:
Without going into excessive detail (which can be found in Miskolczi’s paper), one can easily write down several equations from this diagram alone. First, Miskolczi asserts that P = P0 = 0, so that branch can be ignored altogether. We then have:
AA + K + F = ED + EU,
ST + EU = OLR,
F0 = OLR (the system is in equilibrium),
F0 − F + ED = SG + K,
SG = ST + AA.
To these equations, Miskolczi adds the following:
SG = σTs4 (Stefan-Boltzmann law describing a thermal blackbody surface at temperature Ts),
AA = ED (a much debated application of Kirchoff’s law by Miskolczi, his Eq. 4),
2EU = SG (Miskolczi’s application of the virial theorem),
SG − F0 + ED − EU = OLR (Miskolczi’s energy conservation formula, Eq. 7).
Now the thing is, at this point we actually have 9 equations in the 9 unknowns AA, K, F, ED, EU, ST, SG, F0 and Ts. Although the equations turn out to be not completely independent, only K remains undetermined; in particular, Ts is uniquely determined as
Ts = (3OLR / 2σ)1/4.
Now OLR = F0 = 238 W is known from observation, as it can be calculated from the solar constant and the Earth’s albedo. According to Miskolczi’s algebra, then, the only surface temperature consistent with this is Ts = 281.7 K or about 8.5 degrees Centigrade. This value is uniquely determined without knowing anything about the composition of the atmosphere other than its albedo.
If only climate science were this simple.