I am reading about a new boson.
No, not the (presumed) Higgs boson with a mass of about 126 GeV.
I am reading about a lightweight boson, with a mass of only about 38 MeV, supposedly found at the onetime pride of Soviet science, the Dubna accelerator.
Now Dubna may not have the raw power of the LHC, but the good folks at Dubna are no fools. So if they announce what appears to be a 5-sigma result, one can’t just not pay attention.
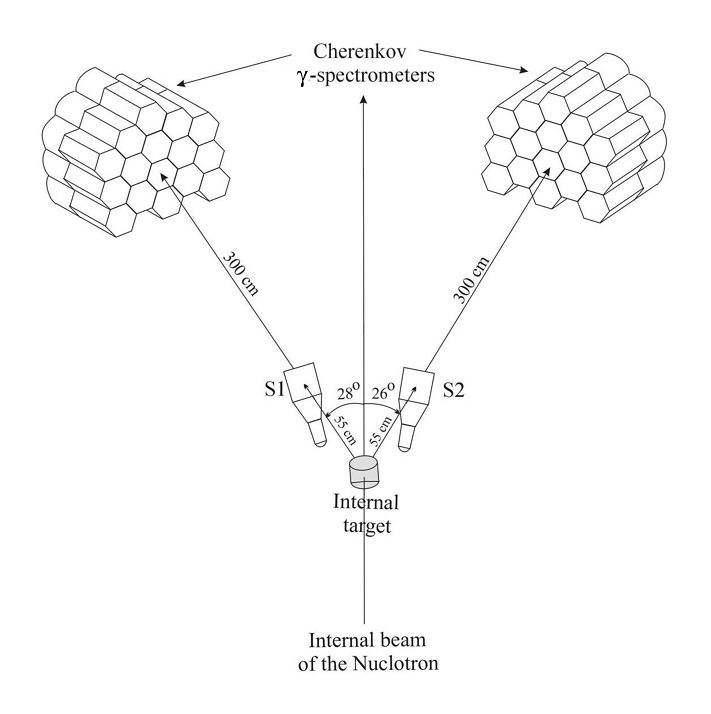
The PHOTON-2 setup. S1 and S2 are scintillation counters. From arXiv:1208.3829.
But a 38 MeV boson? That’s not light, that’s almost featherweight. It’s only about 75 times the mass of the electron, for crying out loud. Less than 4% of the weight of the proton.
The discovery of such a lightweight boson would be truly momentous. It would certainly turn the Standard Model upside down. Whether it is a new elementary particle or some kind of bound state, it is not something that can be fit easily (if at all) within the confines of the Standard Model.
Which is one reason why many are skeptical. This discover is, after all, not unlike that of the presumed Higgs boson, is really just the discovery of a small bump on top of a powerful background of essentially random noise. The statistical significance (or lack thereof) of the bump depends fundamentally on our understanding and accurate modeling of that background.
And it is on the modeling of the background that this recent Dubna announcement has been most severely criticized.
Indeed, in his blog Tommaso Dorigo makes a very strong point of this; he also suggests that the authors’ decision to include far too many decimal digits in error terms is a disturbing sign. Who in his right mind writes 38.4935 ± 1.02639 as opposed to, say, 38.49 ± 1.03?
To this criticism, I would like to offer my own. I am strongly disturbed by the notion of a statistical analysis described by an expression of the type model = data − background. What we should be modeling is not data minus some theoretical background, but the data, period. So the right thing to do is to create a revised model that also includes the background and fit that to the data: model’ = model + background = data. When we do things this way, it is quite possible that the fits are a lot less tight than anticipated, and the apparent statistical significance of a result just vanishes. This is a point I raised a while back in a completely different context: in a paper with John Moffat about the statistical analysis of host vs. satellite galaxies in a large galactic sample.