Someone sent me a link to a YouTube podcast, a segment from an interview with a physicist.
I didn’t like the interview. It was about string theory. My dislike is best illustrated by a point that was made by the speaker. He matter-of-factly noted that, well, math is weird, the sum of \(1 + 2 + 3 + …,\) ad infinitum, is \(-\tfrac{1}{12}.\)
This flawlessly illustrates what bothers me both about the state of theoretical physics and about the way it is presented to general audiences.
No, the sum of all positive integers is not \(-\tfrac{1}{12}.\) Not by a longshot. It is divergent. If you insist, you might say that it is infinite. Certainly not a negative rational number.
But where does this nonsense come from?
Well, there’s the famous Riemann zeta-function. For values of \(s>1,\) it is indeed defined as
$$\zeta(s)=\sum_{n=1}^\infty \frac{1}{n^s}.\tag{1}$$
It is a very interesting function, at the heart of some unresolved problems in mathematics.
But the case of \(s=-1\) (which is when the right-hand side of the equation used to define \(\zeta(s)\) corresponds to the sum of all positive integers) is not an unresolved problem. As it is often presented, it is little more than a dirty trick befitting a cheap stage magician, not a scientist.
That is to say, the above definition of \(\zeta(s),\) as I said, is valid only for \(s>1.\) However, the zeta-function has what is called its analytic continuation, which makes it possible to extend the definition for other values of \(s,\) including \(s=-1.\) This can be accomplished utilizing Riemann’s functional equation, \(\zeta(s)=2^s\pi^{s-1}\sin(\tfrac{1}{2}\pi s)\Gamma(1-s)\zeta(1-s).\) But the right-hand side of (1) in this case does not apply! That sum is valid only when it is convergent, which is to say (again), \(s>1.\)
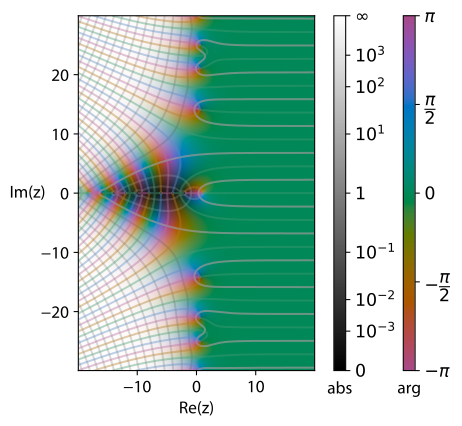
A view of the Riemann zeta-function, from Wikipedia.
So no, the fact that \(\zeta(-1)=-\tfrac{1}{12}\) does not mean that the sum of all integers is \(-\tfrac{1}{12}.\) To suggest otherwise only to dazzle the audience is — looking for a polite term here that nonetheless accurately expresses my disapproval — well, it’s dishonest.
And perhaps unintentionally, it also shows the gap between robust physics and the kind of mathematical games like string theory that pretend to be physics, even though much of it is about mathematical artifacts in 10 dimensions, with at best a very tenuous connection to observable reality.