A popular Internet meme these days is to present an arithmetic expression like, say, 6/3(4−2) and ask the poor souls who follow you to decide the right answer. Soon there will be two camps, each convinced that they know the truth and that the others are illiterate fools: According to one camp, the answer is 4, whereas the other camp will swear that it has to be 1.
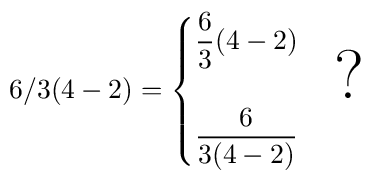
In reality it is neither. Or both. Flip a coin, take your pick. There is no fundamental mathematical truth hidden here. It all boils down to human conventions. The standard convention is that multiplication and division have the same precedence and are evaluated from left to right: So 6/3×(4−2) is pretty unambiguous. But there is another, unwritten convention that when the multiplication sign is omitted, the implied multiplication is assumed to have a higher precedence.
Precisely because of these ambiguities, when you see actual professionals, mathematicians or physicists, write down an expression like this, they opt for clarity: they write, say, (6/3)(4−2) or 6/[3(4−2)] precisely so as to avoid any misunderstanding. Or better yet, they use proper math typesetting software such as LaTeX and write 2D formulas.