What a lovely day.
Once again, I am reading an interesting paper on ArXiv.org (doesn’t matter which one, it wasn’t that interesting) and I notice that the author is a physicist from some Iranian university. ArXiv.org has many papers from Iran. No wonder that nation was able to launch a satellite and is working on a nuclear (weapons?) program, apparently with every hope of success. I am not sympathetic towards the regime of the ayatollahs, but the fact that Iran is not as black-and-white as some would like us to believe must be recognized. I also suspect that another fact, itself somewhat hard to reconcile with the picture of a monolithic, intellectually repressive theocracy, namely that as of 2007, 23 million out of Iran’s 66 million inhabitants had Internet access (according to the CIA World Factbook), has a great deal to do with the success and competence of Iranian physicists.
I remain troubled by this business with black holes.
In particular, the zeroth law. Many authors, such as Wald, say that the zeroth law states that a body’s temperature is constant at equilibrium. I find this formulation less than satisfactory. Thermodynamics is about equilibrium systems to begin with, so it’s not like you have a choice to measure temperatures in a non-equilibrium system; temperature is not even defined there! A proper formulation for the zeroth law is between systems: the idea that an equilibrium exists between systems 1 and 2 expressed in the form of a function f(p1, V1, p2, V2) being zero. Between systems 2 and 3, we have g(p2, V2, p3, V3) = 0, and between systems 3 and 1, we have h(p3, V3, p1, V1) = 0. The zeroth law says that if f(p1, V1, p2, V2) = 0 and g(p2, V2, p3, V3) = 0, then h(p3, V3, p1, V1) = 0. From this, the concept of empirical temperature can be obtained. I don’t see the analog of this for black holes… can we compare two black holes on the basis of J and Ω (which take the place of V and p) and say that they are in “equilibrium”? That makes no sense to me.
On the other hand, if you have a Pfaffian in the form of dA + B dC, there always exists an integrating denominator X (in this simple case, one doesn’t even need Carathéodory’s principle and assume the existence of irreversible processes) such that X dY = dA + B dC. So simply writing down dM – Ω dJ already gives rise to an equation in the form X dY = dM – Ω dJ. That κ and A serve nicely as X and Y may be no more than an interesting coincidence.
But then there is the area theorem such that dA > 0 (just like dS > 0). Is that another coincidence?
And then there is Hawking radiation. The temperature of which is proportional to the surface gravity, T = κ/2π, which is what leads to the identification S = A/4. Too many coincidences?
I don’t know. I can see why this black hole thermodynamics business is not outright stupid, but I remain troubled.
I’m thinking about quantum computers today.
Quantum computers are supposed to be “better” than ordinary digital computers in that they’re able to solve, in polynomial time, many problems that an ordinary digital computer can only solve in exponential time. This has enormous practical implications: notably, many cryptographic methods are based on the fact that there are mathematical problems that can only be solved in exponential time, rendering it impractical to break an encryption key by computer using any “brute force” method. However, if a quantum computer could solve the same problem in polynomial time, a “brute force” method may be practical.
But the thing is, quantum computers are not exactly unique in this respect. Any good old analog computer from the 1950s can also solve the same problems in polynomial time. At least, in principle.
And that’s the operative phrase here: in principle. An analog computer, which represents data in the form of continuous quantities such as lengths, currents, voltages, angles, etc., is limited by its accuracy: even the best analog computer rarely has an accuracy better than one part in a thousand. Not exactly helpful when you’re trying to factorize 1000-digit numbers, for instance.
A quantum computer also represents data in the form of a continuous quantity: the (phase of the) wave function. Like an analog computer, a quantum computer is also limited in accuracy: this limitation is known as decoherence, when the wave function collapses into one of its eigenstates, as if a measurement had been performed.
So why bother with quantum computers, then? Simple: it is widely believed that it is possible to restore coherence in a quantum computer. If this is indeed possible, then a quantum computer is like an analog computer on steroids: any intermediate calculations could be carried out to arbitrary precision, only the final measurement (i.e., reading out the result) would be subject to a classical measurement error, which is not really a big issue when the final result, for instance, is a yes/no type result.
So that’s what quantum computing boils down to: “redundant qubits” that can ensure that coherence is maintained throughout a calculation. Many think that this can be done… I remain somewhat skeptical.
I’m reading Robert Wald’s book, Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics, and I am puzzled. According to Wald, the black hole equivalent of the First Law reads (for a Kerr black hole):
(1/8π)κdA = dM – ΩdJ,
where κ is the surface gravity, A is the area of the event horizon, M is the mass, Ω is the angular velocity of the event horizon, and J is the black hole’s angular momentum.
The analogy with thermodynamics is obvious if one write the First Law as
TdS = dU + pdV,
where T is the temperature, S is the entropy, U is the internal energy, p is the pressure, and V is the volume. Further, as per the black hole area theorem, which Wald proves, A always increases, in analogy with the thermodynamical entropy.
But… if I am to take this analogy seriously, then I am reminded of the fact that in a thermodynamical system the temperature is determined as a function of pressure and volume, i.e., there is a function f such that T = f(p, V). Is there an analogue of this in black hole physics? Is the surface gravity κ fully determined as a function of Ω and J? It is not obvious to me that this is the case, and Wald doesn’t say. Yet without it, there is no zeroth law and no thermodynamics. He does mention the zeroth law in the context of a single black hole having uniform surface gravity, but that’s not good enough. It doesn’t tell me how the surface gravity can be calculated from Ω and J alone, nor does it tell me anything about more than one black hole being involved, whereas in thermodynamics, the zeroth law is about multiple thermodynamical systems being in thermal equilibrium.
Another puzzling aspect is that the area theorem has often been quoted as “proof” that a black hole cannot evaporate. Yet again, if I take the analogy with thermodynamics seriously, the Second Law applies only to closed systems that exchange neither matter nor energy with their environment; it is, in fact, quite possible to reduce S in an open system, otherwise your fridge would not work. So if a black hole can exchange energy and matter with its environment, perhaps it can evaporate after all.
Moreover, for the analogy to be complete, we’d also be required to have
8π∂M/dA = κ,
∂M/∂J = Ω,
just as in ordinary thermodynamics, we have T = ∂U/∂S and p = –∂U/∂V. So, do these relationships hold for black holes?
I guess I’ll go to ArXiv and read some recent papers on black hole thermodynamics.
These are not unusual pictures for us up here in the Great White North:
 |
 |
 |
 |
Trouble is, these pictures are not from Ottawa, Toronto, or London, Ontario. They are from London, England, where it hasn’t stopped snowing yet.
I’m reading a 40-year old book, Methods of Thermodynamics by Howard Reiss. I think I bought it after reading a recommendation on Amazon.com, describing this book as one of the few that takes the idea of axiomatic thermodynamics seriously, and treats it without mixing in concepts from statistical physics or quantum mechanics.
It is a very good book. Not only does it deliver on its promise, it also raises some issues that would not have occurred to me otherwise. For instance, the idea that a so-called equation of state does not fully describe the state of a material, even an ideal gas. You cannot derive U = CvT from the equation of state. You cannot that the internal energy U is a linear function of the temperature T, it has to be postulated.
One thing you can derive from the ideal gas equation of state alone is that an adiabatic expansion must be isothermal. As an ideal gas expands and its volume increases while its pressure decreases, its temperature remains constant. It also made me think again about the cosmological equation of state… cosmologists often play with idealized cases (e.g., dust-filled universe, radiation-filled universe) but until now, I never considered the possibility that even in these idealized cases, the equations of state do not full describe the stuff that they supposedly represent.
Our paper about the thermal analysis of Pioneer 10 and 11 was accepted for publication by Physical Review and it is now on ArXiv.
I think it is an interesting paper. First, it derives from basic principles equations of the thermal recoil force. This is not usually in heat transfer textbooks, as those are more concerned about energy exchange than about momentum. We also derive the infamous factor of 2/3 for a Lambertian (diffuse) surface.
More notably, we make a direct connection between the thermal power of heat sources and the recoil force. The thermal power of heat sources within a spacecraft is usually known very well, and may also be telemetered. So, if a simple formalism exists that gives the recoil force as a function of thermal power, we have a very meaningful way to connect telemetry and trajectory analysis. This is indeed what my “homebrew” orbit determination code does, using Pioneer telemetry and Doppler data together.
No results yet… the paper uses simulated Pioneer 10 data, precisely to avoid jumping to a premature conclusion. We can jump to conclusions once we’re done analyzing all the data using methods that include what’s in this paper… until then, we have to keep an open mind.
In two days, I got two notices of papers being accepted, among them our paper about the possible relationship between modified gravity and the origin of inertia. I am most pleased, because the journal accepting it (MNRAS Letters) is quite prestigious and the paper was a potentially controversial one. The other paper is about Pioneer, and was accepted by Physical Review D. Needless to say, I am pleased.
I’ve read a lot about the coming “digital dark age”, when much of the written record produced by our digital society will no longer be readable due to changing data formats, obsolete hardware, or deteriorating media.
But perhaps, just perhaps, the opposite is happening. Material that is worth preserving may in fact be more likely to survive, simply because it’ll exist in so many copies.
For instance, I was recently citing two books in a paper: one by d’Alembert, written in 1743, and another by Mach, from 1883. Is it pretentious to cite books that you cannot find at any library within a 500-mile radius?
Not anymore, thanks, in this case, to Google Books:
Jean Le Rond d’ Alembert: Traité de dynamique
Ernst Mach: Die Mechanik in ihrer Entwickelung
And now, extra copies of these books exist on my server, as I downloaded and I am preserving the PDFs. Others may do the same, and the books may survive so long as computers exist, as copies are being made and reproduced all the time.
Sometimes, it’s really nice to live in the digital world.
The other day, I put my latest (well, I actually did it last summer, but it’s the latest that has seen the light of day) Pioneer paper on ArXiv.org; it is not about new results (yet), just a confirmation of the Pioneer anomaly using independently developed code, and a demonstration that a jerk term may be present in the data.
Once again, I am studying classical thermodynamics. Axiomatic thermodynamics to be precise, none of this statistical physics business (which is interesting on its own right, but it is quite a different topic.)
The more I learn about it, the more I find thermodynamics incredibly fascinating. Why is it so different from other areas of physics? Perhaps I now have an answer that may be trivial to some, but eluded me until now.
Most of physics is described by functions of coordinates and time. This is true even in the case of general relativity, even as the coordinate system itself may be curved, the curvature (the metric) is described as a function of space-time coordinates.
In contrast, there are no coordinates in axiomatic thermodynamics, only states. States are decribed by state variables, and usually you have these in excess. For instance, the state of one mole of an ideal gas is described by any two of the three variables p (pressure), V (volume) and T (temperature); once two of these are known, the third is given by the ideal gas equation of state, pV = KT, where K is a constant.
Notice that there is no independent variable. The variables p, V, and T are not written as functions of time. Nor should they be, since axiomatic thermodynamics is really equilibrium thermodynamics, and when a system is in equilibrium, it is not changing, its state is constant.
So why is it not called thermostatics? What does dynamics have to do with stationary states? As it turns out, thermodynamics is the science of fitting a square peg in a round hole, as having just established that it’s a science of static states, it nevertheless goes on to explain how states can change… so long as all the intermediate states can exist as static states on their own right, such as when you’re heating a gas slowly enough so that its temperature is more or less uniform at all times, and its state is well approximated by thermodynamic variables.
The zeroeth law states that an empirical temperature exists that is associative: systems that have the same temperature form equivalence classes.
The first law defines the (infinitesimal) quantity of heat dQ as the sum of changes in internal energy (dU) and mechanical work (p dV). An important thing about dQ is that there may not be a Q; in the jargon of differential forms, dQ is a Pfaffian that may not be exact.
The second law uses the assumption of irreversibility and Carathéodory’s theorem to show that there is an integrating denominator T and a function S such that dQ = T dS. (Presto, we have entropy.) Further, T is uniquely determined up to a multiplicative constant.
Combined, the two laws can be written in the form dU = T dS − p dV. After that, much of what is in the textbooks about classical thermodynamics can be written compactly in the form of the Jacobian determinant ∂(T, S)/∂(p, V) = 1.
Given that I know all this, why do I still find myself occasionally baffled by the simplest thermodynamic problems, such as convincing myself that when an isolated system of ideal gas expands, its temperature remains constant? (It does, the math says so, textbooks say so, but still…) There is something uniquely non-trivial about axiomatic thermodynamics.
The other day, arXiv.org split a popular category, astro-ph, into six subcategories. This is convenient… astro-ph, the astrophysics archive, was getting rather large, and the split into sub-categories makes it easier to find papers that are relevant to one’s specialization.
On the other hand… it also means that one is less likely to read papers that are not directly relevant to one’s specialization, but may be interesting, eye-opening, and may help to broaden one’s horizons. Is this a good thing?
There are no easy answers of course… the number of papers just on arXiv.org is mind-boggling (they proudly announced that they’ve passed the half million paper milestone on October, with thousands of new papers added every month) and no one has the time to read them all. Hmmm, perhaps I should have spent more time applauding a recent initiative by Physical Review, their This Week in Physics newsletter and associated Web site.
“John Moffat is not crazy.” These are the opening words of Dan Falk’s new review of John’s book, Reinventing Gravity, which (the review, that is) appeared in the Globe and Mail today. It is an excellent review, and it was a pleasure to see that the sales rank of John’s book immediately went up on amazon.ca. As to the opening sentence… does that mean that I am not crazy either, having worked with John on his gravity theory?
This is what Windows Vista’s weather gadget told me this morning:
Slightly exaggerated
Fortunately, it is lying. It’s only -29 outside, not -35. Still, it made me remember fondly the good ole’ days when there was still some global warming…
Wow. Look at this temperature gradient between Ottawa and Montreal:
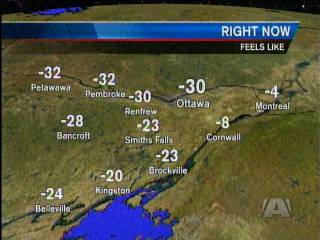
Arctic cold front
And while these are wind chill temperatures, the real thing is soon to follow: some stations forecast a temperature of -33 Centigrade Friday morning. Needless to say, global warming is not exactly high on the list of priorities of most people I know.
Here’s an article worthy of a bookmark:
http://peltiertech.com/Excel/Charts/XYAreaChart2.html
It offers a way to produce a chart in Microsoft Excel much like this one:
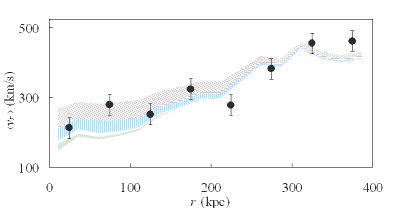
Filled XY area chart
This chart is from something I’m working on, an attempt to test gravitational theories against galaxy survey data.
The link above also comes with a warning: the discussed technique doesn’t work with Excel 2007, due to a (presumably unintentional) change in Excel’s handling of certain complex charts. A pity, but it is also a good example why I am trying to maintain my immunity against chronic upgrade-itis. Two decades ago upgrades were important because they fixed severe bugs and offered serious usability improvements. But today? Why on Earth would I want to upgrade to Office 2007 when Office 2003 does everything I need and more, just so that I can re-learn its user interface? Or make Microsoft richer?
I just read this term, “paparazzi physics”, in Scientific American. Recently, several papers were published on the PAMELA result referencing not a published paper, not even an unpublished draft on arxiv.org, but photographs of a set of slides that were shown during a conference presentation. An appropriate description! But, I think “paparazzi physics” can be used also in a broader sense, describing an alarming trend in the physics community to jump on new results long before they’re corroborated, in order to prove or disprove a theory, conventional or otherwise.
I am starting the new year by reading about a substantial piece of cryptographic work, a successful attack against a widely used cryptographic method for validating secure Web sites, MD5.
That nothing lasts forever is not surprising, and it was always known that cryptographic methods, however strong, may one day be broken as more powerful computers and more clever algorithms become available. What I find astonishing, however, is that even though this particular vulnerability of MD5 has been known theoretically for years, several of the best known Certification Authorities continued to use this broken method to certify secure Web sites. This is hugely irresponsible, and should a real attack actually occur, I’d not be surprised if many lawsuits followed.
The theory behind this attack is complicated, and the hardware is substantial (200 Playstations used as a supercomputing cluster were required to carry out the attack.) One basic reason why the attack was possible in the first place has to do with the “birthday paradox”: it is much easier to construct a fake certificate that has the same signature as a valid certificate than it is to recover the original cryptographic key used to sign the valid certificate.
This has to do with the probability that two persons at a party have the same birthday. For a greater than 50% chance that another person at a party has your birthday, the party has to be huge, with more than 252 guests. However, the probability that at a given party, you find at least two people who share the same birthday (but not necessarily yours) is greater than 50% even for a fairly small party of just over 22 guests.
This apparent paradox is not hard to understand. When you meet another person at a party, the probability that he has the same birthday as you is 1/365 (I’m ignoring leap years here.) The probability that he does NOT have the same birthday as you, then, is 364/365. The probability that two individuals both do NOT have the same birthday as you is the square of this number, (364/365)2. The probability that none of three separate invididuals has the same birthday as you is the cube, (364/365)3. And so on, but you need to go all the way to 253 before this results drops below 0.5, i.e., that the probability that at least one of the people you meet DOES have the same birthday as you becomes greater than 50%.
However, when we relax the condition and no longer require a guest to have the same birthday as you, only that there’s a pair of guests who happen to share their birthday, we need to think in terms of pairs. When there are n guests, they can form n(n – 1)/2 pairs. For 23 guests, the number of pairs they can form is already 253, and therefore, the probability that at least one of these pairs has a shared birthday becomes greater than 50%.
On the cryptographic front, what this basically means is that even as breaking a cryptographic key requires 2k operations, a much smaller number, only 2k/2 is needed to create a rogue cryptographic signature, for instance. It was this fact, combined with other weaknesses of the MD5 algorithm, that allowed these researchers to create a rogue Certification Authority certificate, with which they can go on and create rogue secure certificates for any Web site.
This is a sad picture:
Yesterday, NASA released its final report about the Columbia accident, complete with gruesome but necessary details about how seven astronauts died.

