Mathematics – Page 3

No prize for Perelman

Mar 222010

Imagine solving one of the most profound outstanding problems in mathematics. Imagine living in poverty, in a cockroach-infested apartment in St. Petersburg, Russia. Imagine being awarded one of the world’s most prestigious prizes in science, the Millennium Prize of the Clay Mathematics Institute, which, incidentally, also comes with a cool $1,000,000.

And imagine turning it down. Which is precisely what reclusive Russian mathematician Grigory Perelman apparently did.

I don’t know what to think. Was it a matter of principle for him? Perhaps. But then, he could have indicated in advance that he wouldn’t accept the award, just as he refused to accept the Fields Medal a few years earlier. Why did he keep the world in suspense? Was it posturing? Or is he, hmmm, how can I put this politely, one fry short of a happy meal, to use a favorite phrase of mine from the television series Stargate SG-1?

Symbolics

Computer Algebra, Internet No Responses »

Mar 162010

An interesting anniversary today: 25 years ago, on March 15, 1985, the first ever .com domain name was registered, symbolics.com. The company, in addition to building their own brand of “Lisp Machine” computers, also happened to be selling the commercial version of the MACSYMA computer algebra software. The same software that, in the form of its open-source version, Maxima, continues to evolve thanks to a devoted team of developers… of which I happen to be one.

Alas, Symbolics is no longer, at least not the original company. A privately held company by the same name which obtained much of Symbolics’ assets still sells licenses of the old MACSYMA code.

Random book of the day

Books, Mathematics No Responses »

Dec 292009

There is a fascinating book published by the RAND Corporation, available at Amazon for a mere 81 US dollars. I am tempted to buy it. It must be a fascinating read. Readers’ comments at Amazon are certainly encouraging; while the book has some minor flaws, despite the lack of serious proofreading it is guaranteed not to contain any errors, and it helped at least one reader get to meet the woman who eventually became his wife.

Cubers

Mathematics No Responses »

Aug 152009

I’m watching Cubers on the CBC, a documentary about the revival of interest in Rubik’s Cube, and a recent Rubik’s Cube solvers’ competition. What can I say… it takes me back.

I wouldn’t stand a chance competing in this crowd, but I did win the world’s first (as far as I know) Rubik’s Cube competition, held in Budapest in 1980. I completed my cube in 55 seconds, which wasn’t a very good time by my standards then (I often managed to solve the cube in well under 30 seconds) but it was enough to win.

These days, world class competitors solve the cube in 15 seconds or less. In addition to manual dexterity, such spectacular performances also require memorizing a large number of moves. And then I am not even going to mention the blindfold competitions, involving not just the “standard” 3×3×3 cube but the larger, 4×4×4 and 5×5×5 versions… such skills are hard to comprehend.

I can still solve my (3×3×3) cube without trouble (so long as I am allowed to use my eyes), but I only remember a relatively modest number of moves, which means that my solution is far from efficient. In other words… I am rusty. And my cube is sticky. Literally, it feels sticky on the outside (is the plastic decomposing?) and it’s a bit hard to turn. Still, on the third try, I managed to solve it in a minute an 45 seconds. Not bad, considering that I haven’t touched the thing in years.

Propagandists and statisticians

Mathematics, Politics No Responses »

Jun 242009

I found this gem of a sentence on the Web site of the Embassy of the Islamic Republic of Iran here in Ottawa:

“The Islamic Republic of Iran will register acts of all these states whose records are filled with support for terrorism, pro-colonialist policies for colonizing the oppressed nations, support for the despotic regimes, arming some with weapons of mass destruction and support for anarchy in all parts of the world as disdainful behavior and stipulates that they can not cast doubt on the excellent democratic election held recently in the Islamic Republic of Iran by no means advising them to change their miscalculated approach vis-à-vis the developments having taken place in Iran because designers of the chess game are closely monitoring their behavior and calculating them in the future relations.”

This sentence reminds me of Soviet-era propaganda leaflets. I wonder if the Islamic Republic of Iran has hired propagandists from the former Soviet Union who were left unemployed after 1991.

Anyhow, what exactly are they saying here? Something is wrong with this sentence. They say that,

The Islamic Republic of Iran

will register, as disdainful behavior,

acts of all these states whose records are filled with

support for terrorism,

pro-colonialist policies for colonizing the oppressed nations,

support for the despotic regimes, arming some with weapons of mass destruction and

support for anarchy in all parts of the world

and

stipulates that they can not cast doubt on the excellent democratic election held recently in the Islamic Republic of Iran

by no means advising them to change their miscalculated approach vis-à-vis the developments having taken place in Iran

because

designers of the chess game are closely monitoring their behavior and calculating them in the future relations.

Hmmm… they seem to be telling us that despite all the bad things they say about our disdainful behavior, they are NOT advising us to change our miscalculated approach. The reason for this surprising advice has to do with the designers of the game of chess. Okay, I know that chess may have arrived in Europe from India by way of Persia, but what do the long dead inventors of one of the world’s most popular games have to do with the reelection of Ahmedinejad?

Maybe they are trying to confuse us intentionally, in order to deflect our attention away from a study that suggests that the election was seriously rigged. They really shouldn’t bother. This study says that the election was likely rigged because the final two digits of provincial results show unlikely statistics. But unlikely is not the same as impossible, and unless they can quantify how much more likely this outcome is in a rigged election, the study means nothing; after all, 1-2-3-4-5-6 is as likely to win in a random 6/49 lottery draw as any other number combination, and if they pick these numbers next week, it does not prove fraud by the lottery corporation. For that claim, one would also have to quantify the increased likelihood that a fraudulent draw is more likely to produce the 1-2-3-4-5-6 result when compared to a truly random draw.

Maxima examples

Mathematics, Physics 1 Response »

Jun 082009

Some moderately interesting Maxima examples.

First, this is how we can prove that the covariant derivative of the metric vanishes (but only if the metric is symmetric!)

load(itensor);
imetric(g);
ishow(covdiff(g([],[i,j]),k))$
%,ichr2$
ishow(contract(canform(contract(canform(rename(expand(%)))))))$
ishow(covdiff(g([i,j],[]),k))$
%,ichr2$
ishow(canform(contract(rename(expand(%)))))$
decsym(g,2,0,[sym(all)],[]);
decsym(g,0,2,[],[sym(all)]);
ishow(covdiff(g([],[i,j]),k))$
%,ichr2$
ishow(contract(canform(contract(canform(rename(expand(%)))))))$
ishow(covdiff(g([i,j],[]),k))$
%,ichr2$
ishow(canform(contract(rename(expand(%)))))$

Next, the equation of motion for a perfect fluid:

load(itensor);
imetric(g);
decsym(g,2,0,[sym(all)],[]);
decsym(g,0,2,[],[sym(all)]);
defcon(v,v,u);
components(u([],[]),1);
components(T([],[i,j]),(rho([],[])+p([],[]))*v([],[i])*v([],[j])
                        -p([],[])*g([],[i,j]));
ishow(covdiff(T([],[i,j]),i))$
ishow(canform(%))$
ishow(canform(rename(contract(expand(%)))))$
%,ichr2$
canform(%)$
ishow(canform(rename(contract(expand(%)))))$

Finally, the equation of motion in the spherically symmetric, static case:

load(ctensor);
load(itensor);
K:J([i],[])=covdiff(T([i],[j]),j);
E:ic_convert(K);
ct_coords:[t,r,u,v];
lg:ident(4);
lg[1,1]:B;
lg[2,2]:-A;
lg[3,3]:-r^2;
lg[4,4]:-r^2*sin(u)^2;
depends([A,B,T,rho,p],[r]);
derivabbrev:true;
cmetric();
christof(mcs);
J:[0,0,0,0];
ev(E);
T:ident(4);
T[1,1]:rho;
T[2,2]:T[3,3]:T[4,4]:p;
J,ev;

These examples are probably not profound enough to include with Maxima, but are useful to remember.

Probable probabilities and likely likelihoods

Mathematics, Weather and Climate No Responses »

May 212009

I heard on CBC Newsnet that according the US hurricane center, there is a 50% likelihood that this year will be an average year, hurricane-wise.

I am still pondering whether or not this statement had any information content.

Conspiracies and formal logic

Mathematics, Politics No Responses »

Apr 252009

Watching the outrage over the DHS memos that purportedly target all Americans on the political right as potential enemies of the state, I have come to the realization that a great many political conspiracy theories are based on a trivial error in formal logic: namely, that the implication operator is not commutative.

The implication operator, A → B (A implies B) is true if A is false (B can be anything) or if both A and B are true. In other words, it is only false if A is true but B is false. However, A → B does not imply B → A; the former is true when A is false but B is true, but the latter isn’t.

Yet this is what is at the heart of many conspiracy theories. For instance, a DHS report might say, that those on the fringe of the political right are motivated by the Obama government’s more permissive stance on stem cell research. Some draw the conclusion that this report implies that all who are troubled by Obama’s stance on this issue must be right-wing extremists. I could write this symbolically as follows: we have

member(e, s) → prop(e, p)

where member(e, s) means that e is a member of set s, and prop(e, p) means that e has property p. This symbolic equation cannot be reversed: it does not follow that prop(e, p) → member(e, s).

A closely related mistake is the confusion of the universal and existential operators. The existential operator (usually denoted with an inverted E, but I don’t have an inverted E on my keyboard, so I’ll just use a regular E), E(s, p) says that the set s has at least one member to which property p applies. The universal operator (denoted with an inverted A; I’ll just use a plain A), A(s, p) says that all members of set s have property p. Clearly, the two do not mean the same. Yet all too often, people (on both sides of the political aisle, indeed a lot of the politically correct outrage happens because of this) make this error and assume that once it has been asserted that E(s, p), it is implied that A(s, p). (E.g., a logically flawless statement such as “some blacks are criminals” is assumed to imply the racist generalization that all blacks are criminals.)

One might wonder why formal logic is not taught to would be politicians. I fear that in actuality, the situation is far worse: that they do know formal logic, and use it to their best advantage assuming that you don’t.

Mathematical mysteries

Mathematics No Responses »

Mar 202009

In the Futurama movie, The Beast with a Billion Backs, one scene features a blackboard with two different proofs of the Goldbach conjecture. The Goldback conjecture is one of the oldest unsolved problems in mathematics. One of those problems, like Fermat’s last theorem or the 4-color problem of maps that is deceivingly easy to state and fiendishly hard to prove: that every even number greater than 4 can be expressed as the sum of two primes.

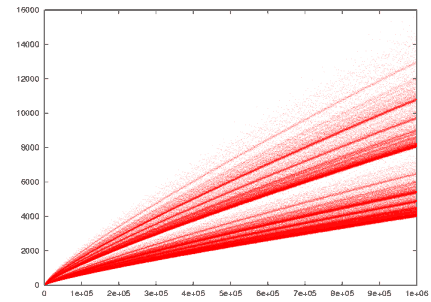
Just how intriguing this problem is, it’s well illustrated by the following plot that shows the number of ways an even number between 4 and 1 million can be split into a sum of two primes:

Golbach partitioning to 1000000

This plot, taken from Wikipedia, clearly shows that the results cluster along curves (asymptotes? attractors?) that follow some kind of a power law with an exponent between ~0.68 and ~0.77, and there may also be some fractal splitting involved, too. This plot is known as Goldbach’s comet. All I have to do is look at it to understand why many people find number theory endlessly fascinating.

Gusztáv Reményi

Mathematics, Personal No Responses »

Feb 162009

I received some sad news yesterday from Hungary: my high school math teacher, Gusztáv Reményi, died last week, at the age of 88. He was a very kind teacher. Our class was a specialized mathematics class, and we were supposed to be the best in the country. In this class, being good at math didn’t just mean that, say, you got sent to national math competitions; you were expected to win them. Perhaps this made Mr. Reményi’s job easier, but I suspect that he would have done well with less talented pupils, too, if not because of his teaching style then due to his personality. If you met him and remembered nothing else, you’d have remembered his smile. I last met him a few years ago, at our high school reunion. He was old, he was frail, but the huge smile was still there, just as I remembered.

About (supposedly) secure Web sites

Cryptography, Internet, Mathematics No Responses »

Jan 012009

I am starting the new year by reading about a substantial piece of cryptographic work, a successful attack against a widely used cryptographic method for validating secure Web sites, MD5.

That nothing lasts forever is not surprising, and it was always known that cryptographic methods, however strong, may one day be broken as more powerful computers and more clever algorithms become available. What I find astonishing, however, is that even though this particular vulnerability of MD5 has been known theoretically for years, several of the best known Certification Authorities continued to use this broken method to certify secure Web sites. This is hugely irresponsible, and should a real attack actually occur, I’d not be surprised if many lawsuits followed.

The theory behind this attack is complicated, and the hardware is substantial (200 Playstations used as a supercomputing cluster were required to carry out the attack.) One basic reason why the attack was possible in the first place has to do with the “birthday paradox”: it is much easier to construct a fake certificate that has the same signature as a valid certificate than it is to recover the original cryptographic key used to sign the valid certificate.

This has to do with the probability that two persons at a party have the same birthday. For a greater than 50% chance that another person at a party has your birthday, the party has to be huge, with more than 252 guests. However, the probability that at a given party, you find at least two people who share the same birthday (but not necessarily yours) is greater than 50% even for a fairly small party of just over 22 guests.

This apparent paradox is not hard to understand. When you meet another person at a party, the probability that he has the same birthday as you is 1/365 (I’m ignoring leap years here.) The probability that he does NOT have the same birthday as you, then, is 364/365. The probability that two individuals both do NOT have the same birthday as you is the square of this number, (364/365)². The probability that none of three separate invididuals has the same birthday as you is the cube, (364/365)³. And so on, but you need to go all the way to 253 before this results drops below 0.5, i.e., that the probability that at least one of the people you meet DOES have the same birthday as you becomes greater than 50%.

However, when we relax the condition and no longer require a guest to have the same birthday as you, only that there’s a pair of guests who happen to share their birthday, we need to think in terms of pairs. When there are n guests, they can form n(n – 1)/2 pairs. For 23 guests, the number of pairs they can form is already 253, and therefore, the probability that at least one of these pairs has a shared birthday becomes greater than 50%.

On the cryptographic front, what this basically means is that even as breaking a cryptographic key requires 2^k operations, a much smaller number, only 2^k/2 is needed to create a rogue cryptographic signature, for instance. It was this fact, combined with other weaknesses of the MD5 algorithm, that allowed these researchers to create a rogue Certification Authority certificate, with which they can go on and create rogue secure certificates for any Web site.

CNN and math literacy

Health, Mathematics, Pop culture, Television No Responses »

Dec 222008

This is not what I usually expect to see when I glance at CNN:

CNN and integrals

It almost makes me believe that we live in a mathematically literate society. If only!

The topic, by the way, was a British Medical Journal paper on brain damage caused by a dancing style called headbanging. I must say, even though I grew up during the disco era, I never much liked dancing. But, for what it’s worth, I not only know how to do integrals, I actually enjoy doing them…

Newer Entries