I just read this term, “paparazzi physics”, in Scientific American. Recently, several papers were published on the PAMELA result referencing not a published paper, not even an unpublished draft on arxiv.org, but photographs of a set of slides that were shown during a conference presentation. An appropriate description! But, I think “paparazzi physics” can be used also in a broader sense, describing an alarming trend in the physics community to jump on new results long before they’re corroborated, in order to prove or disprove a theory, conventional or otherwise.
The prevailing phenomenological theory of modified gravity is MOND, which stands for Modified Newtonian Dynamics. What baffles me is how MOND managed to acquire this status in the first place.
MOND is based on the ad-hoc postulate that the gravitational acceleration of a body in the presence of a weak gravitational field differs from that predicted by Newton. If we denote the Newtonian acceleration with a, MOND basically says that the real acceleration will be a‘ = μ(a/a0)a, where μ(x) is a function such that μ(x) = 1 if x >> 1, and μ(x) = x if μ(x) << 1. Perhaps the simplest example is μ(x) = x/(1+x).
OK, so here is the question that I’d like to ask: Exactly how is this different from the kinds of crank explanations I receive occasionally from strangers writing about the Pioneer anomaly? MOND is no more than an ad-hoc empirical formula that works for galaxies (duh, it was designed to do that) but doesn’t work anywhere else, and all the while it violates such basic principles as energy or momentum conservation. How could the physics community ever take something like MOND seriously?
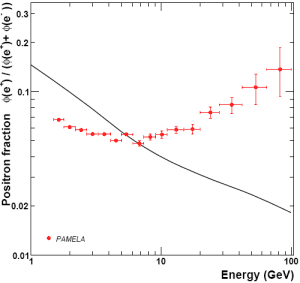
In recent weeks, there has been a lot of discussion in the physics community about a curious observation: an abundance of energetic positrons observed by a satellite named PAMELA. According to some people, this unexpected abundance of positrons is likely caused by annihilation of massive dark matter particles, constituting “smoking gun” evidence that dark matter really exists.
Of course it is possible that this abundance is due to some conventional astrophysics, such as pulsars doing this or that. This is a subject of on-going dispute.
One thing I do not see discussed is that the anticipated behavior is apparently based on a model developed several years ago that uses as many as eleven adjustable parameters yet nevertheless, does not produce a spectacularly good fit of even the low energy data. I wonder if I am missing something.
Looks like Stephen Hawking is coming to Waterloo. I may not be an adoring fan, but I am certainly an admirer: being able to overcome such a debilitating disease and live a creative life is no small accomplishment even when you don’t become a world class theoretical physicist in the process.
A new paper by Sean Carroll asks this question in its title “What if time really exists?” I feel reassurred that Carroll thinks it does (hmmm, let me check my watch… yup, I think it exists, too) but the fact that a paper with this title appears in an archive of theoretical physics papers perhaps illustrates what is so wrong with physics today. To quote Carroll, “when something is so obvious and important, declaring that it isn’t real is sure to win points for boldness”, but have physicists really become this shallow?
I’ve been reading a lot about gauge theories lately. I once wrote what I thought was a fine and concise description of the principle of gauge invariance, but I needed Schrödinger’s equation for it, which made my explanation both non-classical and non-relativistic.
Finally, with the help of a Wikipedia article no less, I think I managed to understand how a gauge theory can come into being without involving any quantum physics. It’s simple, really, surprisingly so.
What you need is a (classical) field theory. A field theory is specified by its Lagrangian, which, crudely speaking, is just the difference between the kinetic and potential energy. For a scalar field φ, the kinetic energy of the field is the square of its gradient, ∂μφ∂μφ. The potential term can be nothing (massless particle in empty space) or it can contain a mass term in the form m2φ2.
Where things begin to get interesting is when we allow φ to be a complex field. In this case, rather than writing φ2, we must now write φφ*, where φ* is the complex conjugate of φ. The same thing happens in the kinetic term. So now the Lagrangian reads,
L = ∂μφ∂μφ* – m2φφ*.
The reason why this is so interesting is that if we change the phase of φ by a set amount (i.e., multiply φ by eiψ) the conjugate’s phase changes by the opposite amount (i.e., φ* it gets multiplied by e–iψ). Their product, therefore, multiplied by eiψe–iψ = 1, remains unchanged. In other words, our Lagrangian is invariant under a global rotation in the complex plane. Right there, this has an important implication: as per Noether’s theorem, a global symmetry implies the existence of a conserved current.
But what if the symmetry is not global but local? Meaning that we rotate φ in the complex plane as before, but the angle of rotation is not the same everywhere? Clearly, φφ* still remains unchaged just as before, but the same is not true for ∂μφ∂μφ*; the derivative operator brings new terms into the Lagrangian.
These new terms are best dealt with by changing the derivative operator into a covariant derivative: ∂μ → Dμ = ∂μ + Aμ, where Aμ is an arbitrary vector field.
Or maybe not so arbitrary. We can make Aμ anything we want, of course, but that also means that we can demand that Aμ satisfy a field equation. Perhaps the field equations of electromagnetism… why not? (After all, every vector field satisfies the field equations of electromagnetism.)
The difference between the original Lagrangian (written using the ordinary derivative ∂μ) and the new Lagrangian (written using the covariant derivative operator Dμ) is the interaction Lagrangian that describes how the φ field interacts with itself through a vector field Aμ. By making the complex φ field locally gauge invariant, we have, in effect, invented the electromagnetic vector potential Aμ.
This is, after all, what gauge theories do: they turn a local symmetry into a force. The local symmetry can be geometric in nature (e.g., a rotation) or it can be an internal symmetry of a field that is not described by simple real numbers. In the present example, the field was made up of complex numbers, and the symmetry was that of the complex plane. This symmetry group is U(1), which is an Abelian group: two rotations in the complex plane, executed one after the other, produce the same result regardless of the order in which they are executed.
In many physically important cases, the symmetry is non-Abelian. The most profound consequence of this is that in place of the gauge field Aμ, which is “inert”, we get gauge field(s) that interact with themselves. In practical terms, when the theory is Abelian, like electromagnetism, the gauge field Aμ represents photons, which are uncharged; but when the theory is non-Abelian, like electroweak theory, the gauge fields are non-Abelian, carry charge, and interact with each other.
The 20th century was the century of weird physics. Weird, mind you, is in the eye of the beholder. Sure, general relativity or quantum mechanics were strange at first, but today, the ideas of invariance, general covariance, or commutator algebras are not at all illogical. More importantly, they work: the predictions of “weird” physics are fully confirmed by experiment.
In contrast, it seems that the physics of the early 21st century is increasingly phantom physics. First, we were told that five sixths if the matter content of the universe is “cold dark matter”, stuff that is invisible and undetectable, as it only interacts with normal matter and with itself gravitationally. Then we were told that all the matter (including dark matter) that is out there is only 30% of the total energy content of the universe, 70% is even more invisible, even more undetectable “dark energy”.
Meanwhile, particle physicists trying to deal with the possibility that the much anticipated Higgs particle will remain undiscovered are toying with the idea that additional particles (which themselves may not be detectable) may cancel out the Higgs boson’s contributions, and thus the Higgs boson would never be detectable. In other words, if I am reading this right, one possibility is that the non-observation of one undetectable particle will be viewed as proof of the existence of another unobserved particle. Wow!
And then I have not even mentioned other undetectable stuff, such as superstrings (too small to ever become detectable by any conceivable experiment), unification (expected to occur at the Planck energy scale, which is forever unreachable by observation), unparticles (yes, there are such animals in the land of theoretical physics), “phantom” matter and energy (I am not making this up), not to mention all the parallel universes of the string theory “landscape”, some of which are populated by “Boltzmann brains” that exist all by themselves, contemplating their existence and inventing imaginary universes around themselves.
I think I prefer the “weird” physics of the 20th century. At least that physics was firmly rooted in what physics is supposedly about, observation and experiment.
Many textbooks and many popular science books tell you that the event horizon, the so-called “point of no return” in the vicinity of a black hole is nothing special. Apart from increasing (but finite!) tidal forces, an observer would not notice anything special when he crosses the horizon. But is this really true?
If this statement were true, it would mean, in essence, that there is no measurement an observer could perform in his immediately vicinity to determine if his vicinity is at or near the event horizon. But this may not be the case; there may, in fact, be a quantity that is measurable (at least in principle).
The curvature of spacetime is described by the Riemann tensor \(R^{\mu\nu\rho\sigma}\). The gradient (covariant derivative) of this quantity is \(R^{\mu\nu\rho\sigma;\kappa}\). Forming the scalar product of this quantity with itself, we obtain an invariant scalar quantity,
\[ K=R^{\mu\nu\rho\sigma;\kappa}R_{\mu\nu\rho\sigma;\kappa}. \]
If we calculate \(K\) for the Schwarzschild metric of a nonrotating, uncharged black hole, we get
\[ K=720m^2\frac{r-2m}{r^9}. \]
This quantity becomes zero and changes sign at the Schwarzschild horizon \(r=2m\).
So never mind what the books say. In principle, an observer can measure the curvature tensor and its gradient, and therefore, can construct an instrument that measures this invariant \(K\). (Note that although I used the letter \(K\), this is not to be confused with the better known Kretchmann invariant.) If this is true, what other effects might there be that make the event horizon a special place?
There is another thing to think about. Often you hear that the Rindler horizon seen by an accelerating observer, or the cosmological horizon in an expanding universe are “just like” the Schwarzschild horizon (perhaps even suggesting that we might be living inside a black hole.) But this cannot be so! Two observers who are not moving the same way do not see the same Rindler horizon or the same cosmological horizon. These are only apparent horizons, their presence, even their existence dependent on the observer’s motion. In contrast, the Schwarzschild horizon is real: two observers can agree on its location regardless of their own location and motion.
I am still evaluating WordPress, but I thought it’d be instructive to write something about physics. (For one thing, it’d allow me to check how well I can include HTML equations in a WordPress post.)
Notably, about neutrino masses. The Standard Model (SM) of particle physics says that neutrinos are massless. Fermions in general are organized into left-handed doublets (with neutrinos and leptons forming one pair, while up-type and down-type quarks forming the other) and right-handed singlets, but there is no right-handed neutrino. An important claim of fame of the SM is that it is a theory that is unitary and renormalizable.
Trouble is, there is now plenty of observational evidence telling us that neutrinos are not massless. Why is that a problem? You take a left-handed neutrino that is massless, and it moves at the speed of light. You take a left-handed neutrino that is massive, and it moves slower than the speed of light. So, you move fast enough to catch up with it, pass it, and look back, and what do you see? A right-handed neutrino, that’s what. But in the SM, no right-handed neutrino exists.
So what happens when you add a right-handed neutrino? There are two basic choices: the neutrino may be represented by either a Majorana spinor or a Dirac spinor. Without going into needless detail, the first choice basically means that the neutrino is its own antiparticle, ν = ν. So why is this a problem? Because neutrinos carry lepton numbers (very simplistically, an electron can be thought of as the sum of a W– particle that carries its electric charge and an electron neutrino that carries its “electronness”. That “electronness” is the lepton number. Now if a neutrino is its own antiparticle, that means that two neutrinos (each carrying a unit of “electronness”) can annihilate, and the two units of “electronness” disappear: lepton number is not conserved. In addition to aesthetic concerns, there are also stringent experimental limits on the violation of lepton number conservation.
The other possibility is that neutrinos are Dirac neutrinos. Dirac neutrinos have genuine antiparticles, so lepton number violation is not a problem. One big problem, however, is the smallness of the neutrino mass; as I understand it, the main objection is that the dimensionless coupling constant that governs the neutrino mass in the Lagrangian is small (of order 10–12) and this worries a lot of people.
Yet another alternative is to account for the observed neutrino oscillations by putting in new interaction terms. While this can be done without a right-handed neutrino, it breaks the renormalizability of the standard model. Loosely speaking, this means that one can no longer assume that things happening at a low energy scale are not affected by things that only happen at high energy. This is not how we experience nature. On the contrary: we can build mechanical devices (relying on low-energy interactions between surface atoms) without worrying about chemistry; we can perform chemical experiments without worrying about nuclear physics; we can do nuclear physics without having to worry about the internal structure of protons and neutrons; and so on. In other words, most physical phenomena can be “renormalized”, treated as if the upper limit of its applicability was infinite, and still yield meaningful results; you only need to worry about higher energy phenomena once you reach that higher energy scale. Why would neutrino physics be different?