Physics – Page 12 – Spinor Info

The right way to think about the Pioneer anomaly

Mar 152009

I often get questions about the Pioneer anomaly and our on-going research. All too often, the questions boil down to this: what percentage of the anomaly can <insert theory here> account for?

This is a very bad way to think about the anomaly. It completely misses the fact that the Pioneer anomaly is not an observed sunward acceleration of the Pioneer spacecraft. The DATA is not a measured acceleration; what is measured is the frequency of the spacecraft’s radio signal.

I already capitalized the word DATA in the previous paragraph; let me also capitalize the words MODEL and RESIDUAL, as these are the right terms to use when thinking about the Pioneer anomaly.

As I said above, the DATA is the Doppler measurement of the spacecraft’s radio frequency.

The MODEL is a model of all forces acting on the spacecraft including gravity, on-board forces, solar pressure, etc; all effects acting on the spacecraft’s radio signal, including the Shapiro delay, solar plasma, the Earth’s atmosphere; and all effects governing the motion of the ground stations participating in the communication.

The RESIDUAL is the error, the difference between the MODEL’s prediction of the Doppler measurement vs. the actual measurement. This RESIDUAL basically appears as noise, but with characteristic signatures (a diurnal and an annual sinusoid along with discontinuous jumps at the time of maneuvers) that suggest mismodeling.

The goal is to make this RESIDUAL “vanish”; by that, we mean that only random noise remains, any diurnal, annual, or maneuver-related signatures are reduced to the level of background noise.

The RESIDUAL can be made to vanish (or at least, can be greatly reduced) by incorporating new contributions into the MODEL. These contributions may or may not be rooted in physics; indeed, orbit determination codes typically have the ability to add “unmodeled” effects (basically, mathematical formulae, such as a term that is a quadratic or exponential function of time) to the MODEL, without regard to the physical origin (if any) of these effects.

Anderson et al. found that if they add an unmodeled constant sunward acceleration to the MODEL, they can make the RESIDUAL vanish. This is the result that has been published as the Pioneer anomaly.

If one has a physical theory that predicts a constant sunward acceleration, it is meaningful to talk in terms of percentages. For instance, one may have a physical theory that predicts a constant sunward acceleration with magnitude cH where c is the speed of light and H is Hubble’s constant at the present epoch; it then makes sense to say that, “using the widely accepted value of H ~= 71 km/s/Mpc, the theory explains 79% of the Pioneer anomaly,” since we’re comparing two numbers that represent the same physical quantity, a constant sunward acceleration.

However, note (very important!) that the fact that a constant sunward acceleration fits the data does not exclude alternatives with forces that are not constant or sunward pointing; the DATA admits many different MODELs.

Now let’s talk about the thermal recoil force. It is NOT constant and it is NOT sunward pointing. As we recompute this force, incorporating the best thermal model that we can compute into the MODEL and re-evaluate it, we obtain a new RESIDUAL. There are, then, the following possibilities:

Suppose that the new RESIDUAL is as free of a mismodeling signature as the constant acceleration model and that its magnitude cannot be reduced by adding any unmodeled effects (i.e., we reached the level of our basic measurement noise.) Does it then make sense to speak of percentages? OK, so the thermal recoil force is 30%, 70%, 130%, you name it, of the constant sunward acceleration. But the thermal recoil force is neither constant nor sunward, and by incorporating it into the MODEL, we got a different trajectory than the constant sunward acceleration cas. Yet the RESIDUAL vanishes, so the MODEL fits the DATA just as well.
Suppose that the new RESIDUAL is half the original RESIDUAL at least insofar as the apparent mismodeling is concerned. What does this mean? Does this mean that the thermal recoil force and the resulting acceleration is half that of the constant sunward value? Most certainly not. Say it’s 65%. Now did we explain 50% of the anomaly (by reducing the RESIDUAL to 50%) or did we explain 65% of the anomaly (by producing a thermal recoil acceleration that’s 65% of the published constant sunward value?)

Instead of playing with percentages, it makes a lot more sense to do this: after applying our best present understanding insofar as thermal recoil forces are concerned, we re-evaluate the MODEL. We compute the RESIDUAL. We check if this residual contains any signatures of mismodeling. If it doesn’t, we have no anomaly. If it does, we characterize this mismodeling by applying various unmodeled effects (e.g., a constant sunward force, exponential decay, etc.) to check if any of these can characterize the RESIDUAL. We then report on the existence of a (revised) anomaly with the formula for the unmodeled effect as a means to consisely characterize the RESIDUAL. If this revised anomaly is still well described by a constant sunward term, we may use a percentage figure to describe it… otherwise, it’s probably not helpful to do so.

Einstein and Silberstein, Part 2

Physics No Responses »

Mar 102009

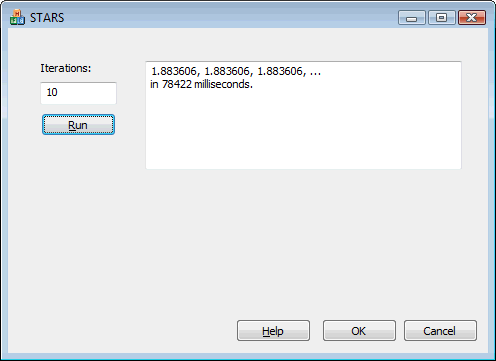
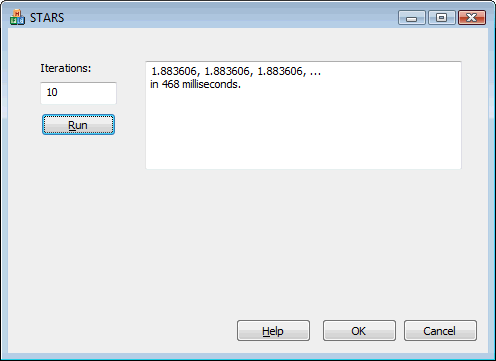
Einstein was right and Silberstein was wrong, but it’s beautifully subtle why.

Einstein’s point was that in a region free of singularities, the circumference of an infinitesimal circle should be 2π times its radius. He then showed that an infinitesimal circle perpendicular to, and centered around, the line connecting the two mass points in Silberstein’s solution has the wrong radius, hence the line connecting the two masses must be singular.

Silberstein countered by pointing out an error in Einstein’s derivation and then showing that a particular quantity rigorously vanishes along this line, implying that yes, the circumference of the infinitesimal circles in question do, in fact, have the right radii. This solution appeared in his paper in Physical Review in 1936.

Einstein then, in his published Letter that he wrote in reply to Silberstein’s paper, provided a technical argument discussing square roots and derivatives that, while correct, is not very enlightening. (It’s one of those comments that make perfect sense once you know what the devil he is talking about, but there’s no possible way you can actually understand what he’s talking about from the comment alone. Not that I haven’t been guilty of committing the same sin, even writing things that I myself wasn’t able to understand a few months later without going back to my notes or calculations. But I digress.)

By solving for the metric and obtaining an explicit formula, I was able to better understand this mystery.

First, it should be noted that the axis connecting the two mass points is also the origin of the radial coordinate, so the coordinate system itself is singular here even if there is no physical singularity. To verify that there is no physical singularity at this location, we can draw tiny, infinitesimal circles centered around this axis and check if they obey the rules of Euclidean geometry (one fundamental rule in curved spacetime is that in a small enough region, things always look Euclidean.) This was the basis of Einstein’s argument.

We can express the ratio of the angular and radial components of the metric in the form of an exponential expression, say exp(N) where N is some expression. Clearly, we must have N(r → 0) = 0 in order for the circumference of an infinitesimal circle centered around the axis to be 2π its radius.

As it turns out, N appears in the form [] + C where [] is just some complicated expression. It turns out that this part [] is constant along the axis, but its constant value is different between the two mass points vs. outside the mass points. I can draw the axis and the two mass points like this:

––––––––––––––––X––––––––––––––––X––––––––––––––––

The bracketed expression is constant along this line (not constant outside the line, such as above or below it but that’s not relevant now) but has one constant value between the two points (the two X’s) and another constant value on the two sides. The two constant values are not the same.

We can choose the constant C to make N vanish either between the two mass points or outside the two mass points but not both at the same time. When N vanishes outside, but not between, the two mass points, the singularity that remains serves as a “strut” holding the two mass points apart:

––––––––––––––––X================X––––––––––––––––

Or, when N vanishes outside, it’s as if the two mass points were attached by “ropes” to the “sphere at infinity”, hanging from there in static equilibrium as gravity pulls them together:

================X––––––––––––––––X================

So how come Silberstein was able to dismiss Einstein’s criticism? He was able to do so by making a particular choice of the sign of a square root that made N vanish both between and outside the two mass points. But this is where it helps to write N in the form that I obtained, symbolically as [] + C, with the bracketed part having one constant value along the axis between the two masses and another value outside. Sure we can make N vanish everywhere along the axis… by allowing C to have different values between vs. outside the masses.

This is fine along the axis… the masses themselves are singularities, so they represent a discontinuity anyway, so we are free to choose different integration constants on two sides of a discontinuity. This is indeed what Silberstein has done by choosing a particular sign of a square root in his formulation of the metric.

But, as Einstein pointed out, such a choice of sign leads to a discontinuity in derivatives. More explicitly, what happens is that the function N is defined not just along the axis but everywhere in spacetime… to get from a point on the axis between the two masses to a point outside, we need not go along the axis, we can leave the axis, go around the mass, and then return to the axis. As we do this, we encounter no singularity but the value of C must jump from one constant to another at some point. In other words, by removing the “strut” or “rope” singularity from the axis, we introduced a much worse singular “membrane” that separates regions of space.

One morale of this story is that when we use a coordinate system like polar coordinates that is not well defined at the origin, we must be ultra careful about that spot… since the coordinate system is singular here, this is where things can go wrong even if they appear perfect everywhere else.

Einstein and Silberstein

Physics No Responses »

Mar 102009

I’m reading about the debate in the 1930s between Einstein and Silberstein about the (non-)existence of a static two-body vacuum solution of the Einstein field equations.

Silberstein claimed to have found just such a solution as a special case of Weyl’s metric. However, he then concluded that the existence of an unphysical solution implies that Einstein’s gravitational theory has to be modified.

Meanwhile, Einstein dismissed Silberstein’s solution on two grounds. First, he claimed that there are additional singularities; second, he claimed that a solution that yields singularities is in any case not a proper solution of a field theory, so it certainly cannot be used to discredit that theory.

I disagree with Silberstein… just because there exist solutions that are unphysical does not unmake a theory. The equations of ballistics also yield unphysical solutions, such as cannonballs going underground or flying backwards in time… but it simply means that we chose unphysical initial conditions, not that the theory is wrong.

I also disagree with Einstein’s second argument though… field theory or not, some singularities can be quite useful and physically meaningful, be it, say, the “point mass” in Newton’s theory, the “point source” in electromagnetism, or, well, singularities in general relativity representing compact (point) masses.

But both these issues are more philosophy than physics. I am more interested in Einstein’s first argument… is it really true that Silberstein’s solution yields more than two singularities?

That is because when I actually calculate with Silberstein’s metric, I find regular behavior everywhere except at the two singular points. I see no sign whatsoever of the supposed singular line between them. What am I missing?

Iranian physics

Physics, Politics No Responses »

Feb 122009

Once again, I am reading an interesting paper on ArXiv.org (doesn’t matter which one, it wasn’t that interesting) and I notice that the author is a physicist from some Iranian university. ArXiv.org has many papers from Iran. No wonder that nation was able to launch a satellite and is working on a nuclear (weapons?) program, apparently with every hope of success. I am not sympathetic towards the regime of the ayatollahs, but the fact that Iran is not as black-and-white as some would like us to believe must be recognized. I also suspect that another fact, itself somewhat hard to reconcile with the picture of a monolithic, intellectually repressive theocracy, namely that as of 2007, 23 million out of Iran’s 66 million inhabitants had Internet access (according to the CIA World Factbook), has a great deal to do with the success and competence of Iranian physicists.

More on black hole mechanics

Physics No Responses »

Feb 072009

I remain troubled by this business with black holes.

In particular, the zeroth law. Many authors, such as Wald, say that the zeroth law states that a body’s temperature is constant at equilibrium. I find this formulation less than satisfactory. Thermodynamics is about equilibrium systems to begin with, so it’s not like you have a choice to measure temperatures in a non-equilibrium system; temperature is not even defined there! A proper formulation for the zeroth law is between systems: the idea that an equilibrium exists between systems 1 and 2 expressed in the form of a function f(p₁, V₁, p₂, V₂) being zero. Between systems 2 and 3, we have g(p₂, V₂, p₃, V₃) = 0, and between systems 3 and 1, we have h(p₃, V₃, p₁, V₁) = 0. The zeroth law says that if f(p₁, V₁, p₂, V₂) = 0 and g(p₂, V₂, p₃, V₃) = 0, then h(p₃, V₃, p₁, V₁) = 0. From this, the concept of empirical temperature can be obtained. I don’t see the analog of this for black holes… can we compare two black holes on the basis of J and Ω (which take the place of V and p) and say that they are in “equilibrium”? That makes no sense to me.

On the other hand, if you have a Pfaffian in the form of dA + B dC, there always exists an integrating denominator X (in this simple case, one doesn’t even need Carathéodory’s principle and assume the existence of irreversible processes) such that X dY = dA + B dC. So simply writing down dM – Ω dJ already gives rise to an equation in the form X dY = dM – Ω dJ. That κ and A serve nicely as X and Y may be no more than an interesting coincidence.

But then there is the area theorem such that dA > 0 (just like dS > 0). Is that another coincidence?

And then there is Hawking radiation. The temperature of which is proportional to the surface gravity, T = κ/2π, which is what leads to the identification S = A/4. Too many coincidences?

I don’t know. I can see why this black hole thermodynamics business is not outright stupid, but I remain troubled.

Quantum computing and decoherence

Computers, Physics No Responses »

Feb 062009

I’m thinking about quantum computers today.

Quantum computers are supposed to be “better” than ordinary digital computers in that they’re able to solve, in polynomial time, many problems that an ordinary digital computer can only solve in exponential time. This has enormous practical implications: notably, many cryptographic methods are based on the fact that there are mathematical problems that can only be solved in exponential time, rendering it impractical to break an encryption key by computer using any “brute force” method. However, if a quantum computer could solve the same problem in polynomial time, a “brute force” method may be practical.

But the thing is, quantum computers are not exactly unique in this respect. Any good old analog computer from the 1950s can also solve the same problems in polynomial time. At least, in principle.

And that’s the operative phrase here: in principle. An analog computer, which represents data in the form of continuous quantities such as lengths, currents, voltages, angles, etc., is limited by its accuracy: even the best analog computer rarely has an accuracy better than one part in a thousand. Not exactly helpful when you’re trying to factorize 1000-digit numbers, for instance.

A quantum computer also represents data in the form of a continuous quantity: the (phase of the) wave function. Like an analog computer, a quantum computer is also limited in accuracy: this limitation is known as decoherence, when the wave function collapses into one of its eigenstates, as if a measurement had been performed.

So why bother with quantum computers, then? Simple: it is widely believed that it is possible to restore coherence in a quantum computer. If this is indeed possible, then a quantum computer is like an analog computer on steroids: any intermediate calculations could be carried out to arbitrary precision, only the final measurement (i.e., reading out the result) would be subject to a classical measurement error, which is not really a big issue when the final result, for instance, is a yes/no type result.

So that’s what quantum computing boils down to: “redundant qubits” that can ensure that coherence is maintained throughout a calculation. Many think that this can be done… I remain somewhat skeptical.

Black hole thermodynamics

Physics 1 Response »

Feb 032009

I’m reading Robert Wald’s book, Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics, and I am puzzled. According to Wald, the black hole equivalent of the First Law reads (for a Kerr black hole):

(1/8π)κdA = dM – ΩdJ,

where κ is the surface gravity, A is the area of the event horizon, M is the mass, Ω is the angular velocity of the event horizon, and J is the black hole’s angular momentum.

The analogy with thermodynamics is obvious if one write the First Law as

TdS = dU + pdV,

where T is the temperature, S is the entropy, U is the internal energy, p is the pressure, and V is the volume. Further, as per the black hole area theorem, which Wald proves, A always increases, in analogy with the thermodynamical entropy.

But… if I am to take this analogy seriously, then I am reminded of the fact that in a thermodynamical system the temperature is determined as a function of pressure and volume, i.e., there is a function f such that T = f(p, V). Is there an analogue of this in black hole physics? Is the surface gravity κ fully determined as a function of Ω and J? It is not obvious to me that this is the case, and Wald doesn’t say. Yet without it, there is no zeroth law and no thermodynamics. He does mention the zeroth law in the context of a single black hole having uniform surface gravity, but that’s not good enough. It doesn’t tell me how the surface gravity can be calculated from Ω and J alone, nor does it tell me anything about more than one black hole being involved, whereas in thermodynamics, the zeroth law is about multiple thermodynamical systems being in thermal equilibrium.

Another puzzling aspect is that the area theorem has often been quoted as “proof” that a black hole cannot evaporate. Yet again, if I take the analogy with thermodynamics seriously, the Second Law applies only to closed systems that exchange neither matter nor energy with their environment; it is, in fact, quite possible to reduce S in an open system, otherwise your fridge would not work. So if a black hole can exchange energy and matter with its environment, perhaps it can evaporate after all.

Moreover, for the analogy to be complete, we’d also be required to have

8π∂M/dA = κ,
∂M/∂J = Ω,

just as in ordinary thermodynamics, we have T = ∂U/∂S and p = –∂U/∂V. So, do these relationships hold for black holes?

I guess I’ll go to ArXiv and read some recent papers on black hole thermodynamics.

Equations of state

Physics No Responses »

Jan 302009

I’m reading a 40-year old book, Methods of Thermodynamics by Howard Reiss. I think I bought it after reading a recommendation on Amazon.com, describing this book as one of the few that takes the idea of axiomatic thermodynamics seriously, and treats it without mixing in concepts from statistical physics or quantum mechanics.

It is a very good book. Not only does it deliver on its promise, it also raises some issues that would not have occurred to me otherwise. For instance, the idea that a so-called equation of state does not fully describe the state of a material, even an ideal gas. You cannot derive U = C_vT from the equation of state. You cannot that the internal energy U is a linear function of the temperature T, it has to be postulated.

One thing you can derive from the ideal gas equation of state alone is that an adiabatic expansion must be isothermal. As an ideal gas expands and its volume increases while its pressure decreases, its temperature remains constant. It also made me think again about the cosmological equation of state… cosmologists often play with idealized cases (e.g., dust-filled universe, radiation-filled universe) but until now, I never considered the possibility that even in these idealized cases, the equations of state do not full describe the stuff that they supposedly represent.

Pioneer thermal analysis

Physics No Responses »

Jan 302009

Our paper about the thermal analysis of Pioneer 10 and 11 was accepted for publication by Physical Review and it is now on ArXiv.

I think it is an interesting paper. First, it derives from basic principles equations of the thermal recoil force. This is not usually in heat transfer textbooks, as those are more concerned about energy exchange than about momentum. We also derive the infamous factor of 2/3 for a Lambertian (diffuse) surface.

More notably, we make a direct connection between the thermal power of heat sources and the recoil force. The thermal power of heat sources within a spacecraft is usually known very well, and may also be telemetered. So, if a simple formalism exists that gives the recoil force as a function of thermal power, we have a very meaningful way to connect telemetry and trajectory analysis. This is indeed what my “homebrew” orbit determination code does, using Pioneer telemetry and Doppler data together.

No results yet… the paper uses simulated Pioneer 10 data, precisely to avoid jumping to a premature conclusion. We can jump to conclusions once we’re done analyzing all the data using methods that include what’s in this paper… until then, we have to keep an open mind.

Papers

Physics No Responses »

Jan 292009

In two days, I got two notices of papers being accepted, among them our paper about the possible relationship between modified gravity and the origin of inertia. I am most pleased, because the journal accepting it (MNRAS Letters) is quite prestigious and the paper was a potentially controversial one. The other paper is about Pioneer, and was accepted by Physical Review D. Needless to say, I am pleased.

No digital dark ages?

Books, Internet, Physics, Society, Technology No Responses »

Jan 272009

I’ve read a lot about the coming “digital dark age”, when much of the written record produced by our digital society will no longer be readable due to changing data formats, obsolete hardware, or deteriorating media.

But perhaps, just perhaps, the opposite is happening. Material that is worth preserving may in fact be more likely to survive, simply because it’ll exist in so many copies.

For instance, I was recently citing two books in a paper: one by d’Alembert, written in 1743, and another by Mach, from 1883. Is it pretentious to cite books that you cannot find at any library within a 500-mile radius?

Not anymore, thanks, in this case, to Google Books:

Jean Le Rond d’ Alembert: Traité de dynamique
Ernst Mach: Die Mechanik in ihrer Entwickelung

And now, extra copies of these books exist on my server, as I downloaded and I am preserving the PDFs. Others may do the same, and the books may survive so long as computers exist, as copies are being made and reproduced all the time.

Sometimes, it’s really nice to live in the digital world.

Pioneer paper

Physics 1 Response »

Jan 262009

The other day, I put my latest (well, I actually did it last summer, but it’s the latest that has seen the light of day) Pioneer paper on ArXiv.org; it is not about new results (yet), just a confirmation of the Pioneer anomaly using independently developed code, and a demonstration that a jerk term may be present in the data.

Thermodynamics (again)

Physics 1 Response »

Jan 242009

Once again, I am studying classical thermodynamics. Axiomatic thermodynamics to be precise, none of this statistical physics business (which is interesting on its own right, but it is quite a different topic.)

The more I learn about it, the more I find thermodynamics incredibly fascinating. Why is it so different from other areas of physics? Perhaps I now have an answer that may be trivial to some, but eluded me until now.

Most of physics is described by functions of coordinates and time. This is true even in the case of general relativity, even as the coordinate system itself may be curved, the curvature (the metric) is described as a function of space-time coordinates.

In contrast, there are no coordinates in axiomatic thermodynamics, only states. States are decribed by state variables, and usually you have these in excess. For instance, the state of one mole of an ideal gas is described by any two of the three variables p (pressure), V (volume) and T (temperature); once two of these are known, the third is given by the ideal gas equation of state, pV = KT, where K is a constant.

Notice that there is no independent variable. The variables p, V, and T are not written as functions of time. Nor should they be, since axiomatic thermodynamics is really equilibrium thermodynamics, and when a system is in equilibrium, it is not changing, its state is constant.

So why is it not called thermostatics? What does dynamics have to do with stationary states? As it turns out, thermodynamics is the science of fitting a square peg in a round hole, as having just established that it’s a science of static states, it nevertheless goes on to explain how states can change… so long as all the intermediate states can exist as static states on their own right, such as when you’re heating a gas slowly enough so that its temperature is more or less uniform at all times, and its state is well approximated by thermodynamic variables.

The zeroeth law states that an empirical temperature exists that is associative: systems that have the same temperature form equivalence classes.

The first law defines the (infinitesimal) quantity of heat dQ as the sum of changes in internal energy (dU) and mechanical work (p dV). An important thing about dQ is that there may not be a Q; in the jargon of differential forms, dQ is a Pfaffian that may not be exact.

The second law uses the assumption of irreversibility and Carathéodory’s theorem to show that there is an integrating denominator T and a function S such that dQ = T dS. (Presto, we have entropy.) Further, T is uniquely determined up to a multiplicative constant.

Combined, the two laws can be written in the form dU = T dS − p dV. After that, much of what is in the textbooks about classical thermodynamics can be written compactly in the form of the Jacobian determinant ∂(T, S)/∂(p, V) = 1.

Given that I know all this, why do I still find myself occasionally baffled by the simplest thermodynamic problems, such as convincing myself that when an isolated system of ideal gas expands, its temperature remains constant? (It does, the math says so, textbooks say so, but still…) There is something uniquely non-trivial about axiomatic thermodynamics.

Convenience or excess specialization?

Physics No Responses »

Jan 222009

The other day, arXiv.org split a popular category, astro-ph, into six subcategories. This is convenient… astro-ph, the astrophysics archive, was getting rather large, and the split into sub-categories makes it easier to find papers that are relevant to one’s specialization.

On the other hand… it also means that one is less likely to read papers that are not directly relevant to one’s specialization, but may be interesting, eye-opening, and may help to broaden one’s horizons. Is this a good thing?

There are no easy answers of course… the number of papers just on arXiv.org is mind-boggling (they proudly announced that they’ve passed the half million paper milestone on October, with thousands of new papers added every month) and no one has the time to read them all. Hmmm, perhaps I should have spent more time applauding a recent initiative by Physical Review, their This Week in Physics newsletter and associated Web site.

John Moffat is not crazy

Books, Physics No Responses »

Jan 182009

“John Moffat is not crazy.” These are the opening words of Dan Falk’s new review of John’s book, Reinventing Gravity, which (the review, that is) appeared in the Globe and Mail today. It is an excellent review, and it was a pleasure to see that the sales rank of John’s book immediately went up on amazon.ca. As to the opening sentence… does that mean that I am not crazy either, having worked with John on his gravity theory?

Paparazzi physics?

Physics No Responses »

Jan 032009

I just read this term, “paparazzi physics”, in Scientific American. Recently, several papers were published on the PAMELA result referencing not a published paper, not even an unpublished draft on arxiv.org, but photographs of a set of slides that were shown during a conference presentation. An appropriate description! But, I think “paparazzi physics” can be used also in a broader sense, describing an alarming trend in the physics community to jump on new results long before they’re corroborated, in order to prove or disprove a theory, conventional or otherwise.

Why MOND?

Physics No Responses »

Dec 082008

The prevailing phenomenological theory of modified gravity is MOND, which stands for Modified Newtonian Dynamics. What baffles me is how MOND managed to acquire this status in the first place.

MOND is based on the ad-hoc postulate that the gravitational acceleration of a body in the presence of a weak gravitational field differs from that predicted by Newton. If we denote the Newtonian acceleration with a, MOND basically says that the real acceleration will be a‘ = μ(a/a₀)a, where μ(x) is a function such that μ(x) = 1 if x >> 1, and μ(x) = x if μ(x) << 1. Perhaps the simplest example is μ(x) = x/(1+x).

OK, so here is the question that I’d like to ask: Exactly how is this different from the kinds of crank explanations I receive occasionally from strangers writing about the Pioneer anomaly? MOND is no more than an ad-hoc empirical formula that works for galaxies (duh, it was designed to do that) but doesn’t work anywhere else, and all the while it violates such basic principles as energy or momentum conservation. How could the physics community ever take something like MOND seriously?

Anomalous positrons: a smoking gun for dark matter?

Physics No Responses »

Dec 022008

In recent weeks, there has been a lot of discussion in the physics community about a curious observation: an abundance of energetic positrons observed by a satellite named PAMELA. According to some people, this unexpected abundance of positrons is likely caused by annihilation of massive dark matter particles, constituting “smoking gun” evidence that dark matter really exists.

Of course it is possible that this abundance is due to some conventional astrophysics, such as pulsars doing this or that. This is a subject of on-going dispute.

One thing I do not see discussed is that the anticipated behavior is apparently based on a model developed several years ago that uses as many as eleven adjustable parameters yet nevertheless, does not produce a spectacularly good fit of even the low energy data. I wonder if I am missing something.

$PAMELA positron fraction and theoretical models.$

PAMELA positron fraction and theoretical models.

Hawking in Waterloo…

Physics No Responses »

Nov 282008

Looks like Stephen Hawking is coming to Waterloo. I may not be an adoring fan, but I am certainly an admirer: being able to overcome such a debilitating disease and live a creative life is no small accomplishment even when you don’t become a world class theoretical physicist in the process.

The existence of time

Physics No Responses »

Nov 252008

A new paper by Sean Carroll asks this question in its title “What if time really exists?” I feel reassurred that Carroll thinks it does (hmmm, let me check my watch… yup, I think it exists, too) but the fact that a paper with this title appears in an archive of theoretical physics papers perhaps illustrates what is so wrong with physics today. To quote Carroll, “when something is so obvious and important, declaring that it isn’t real is sure to win points for boldness”, but have physicists really become this shallow?

Older Entries Newer Entries